Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование математических методов в животноводстве и ветеринарииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ И БИОТЕХНОЛОГИИ имени К.И. СКРЯБИНА»
Федькина Т. В.
Использование математических методов в животноводстве и ветеринарии
Учебно – методическое пособие
Москва 2010
Федькина, Т. В. Использование математических методов в животноводстве и ветеринарии: учеб.-метод. пособие / Т. В. Федькина. – М.: ФГОУ ВПО МГАВМиБ им. К. И. Скрябина, 2010. – 93 с.
Пособие представляет собой учебно-методический комплекс, объединяющий теоретический материал, задачи и приложение MS Excel к биометрическим расчетам. Учебно-методическое пособие подготовлено в соответствии с Федеральным государственным образовательным стандартом высшего профессионального образования. Рекомендовано для студентов квалификации «бакалавр» по направлениям подготовки: 020400 – «Биология», 111100 – «Зоотехния», 111900 – «Ветсанэкспертиза».
Рецензенты: Скрипниченко Г. Г., д. б. н., профессор (МГАВМиБ), Барашев В. П., к. ф. - м. н., доцент (МИРЭА).
Эксперт: Никишов А. А., к. с. - х. н., доцент (РУДН)
Утверждено на заседании учебно - методической комиссии ветеринарно – биологического факультета ФГОУ ВПО МГАВМиБ (протокол № 6 от 20 апреля 2010 г.)
ОГЛАВЛЕНИЕ Стр. Предисловие…………………………………………………………………… 4 1. Элементы теории вероятностей…………………………………………… 5 1.1 Случайные величины. Вероятность случайного события……………. 5 1.2 Закон распределения дискретной случайной величины……………... 5 1.3 Интегральная функция распределения………………………………… 6 1.4 Дифференциальная функция распределения………………………….. 7 1.5 Равномерное распределение непрерывной случайной величины……. 8 1.6 Числовые характеристики случайных величин………………………... 9 1.7 Нормальный закон распределения вероятностей случайной величины.12 2. Элементы математической статистики……………………………………. 15 2.1 Предмет и задачи математической статистики………………………... 15 2.2 Генеральная и выборочная совокупности……………………………… 16 2.3 Графическое представление статистических рядов…………………… 17 2.4 Выборочные характеристики…………………………………………… 21 2.4.1 Средние величины………………………………………………… 21 2.4.2 Выборочные центральные моменты. Асимметрия и эксцесс…... 25 2.4.3 Показатели вариации……………………………………………… 27 2.4.4 Степень свободы…………………………………………………… 30 2.5 Статистические оценки параметров распределения………………….. 30 2.6 Функции и распределения в математической статистике……………. 33 2.6.1 Распределение хи-квадрат ( 2.6.2 Статистические гипотезы. Критерии согласия…………………... 35 2.6.3 Критерий согласия 2.6.4 Распределение Стьюдента…………………………………………. 41 2.6.5 Распределение Фишера…………………………………………….. 43 2.7 Доверительные интервалы………………………………………………. 45 2.8 Элементы линейного регрессионного и корреляционного анализа…... 48 2.8.1 Элементы корреляционной зависимости. Коэффициент корреляции……………………………………………………………………. 48 2.8.2 Линейная регрессия. Коэффициенты регрессии…………………..53 2.9 Критерии достоверности выборочных показателей………………….. 55 2.10 Элементы дисперсионного анализа…………………………………… 60 2.10.1 Однофакторный дисперсионный анализ…………………………61 2.10.2 Двухфакторный дисперсионный анализ.……………………….. 65 3. MS Excel в статистике……. …………………………………………………69 3.1. Интервальный и дискретный вариационный ряд. Графическое представление статистических рядов…………………… 70 3.2. Описательная статистика…………………………………………… 74 3.3. Корреляционный анализ ……………………………………………. 77 3.4. Дисперсионный анализ……………………………………………… 79 Приложения…………………………………………………………………….. 84 Литература……………………………………………………………………… 93 Предисловие Курс теории вероятностей и математической статистики входит в цикл фундаментальных дисциплин, изучение которых является обязательным для студентов сельскохозяйственных учебных заведений. Одной из важнейших сфер приложения теории вероятностей и математической статистики является животноводство. Развитие современного животноводства сопровождается накоплением большого количества информации по многим вопросам генетики, селекции, продуктивности, здоровья животных, поведенческих функций и т.д. В задачу науки входят классификация, упорядочение и систематизация этих данных, их научный анализ. Подобный подход позволяет формулировать практические предложения, способствующие ускорению развития тех или иных отраслей животноводства, совершенствовать и создавать новые перспективные отрасли, прогнозировать развитие того или иного направления. В ветеринарии, дополнительно к перечисленным возможностям, использование научного анализа позволяет теоретически моделировать течение болезни или действия лечебных факторов и разрабатывать методы профилактики и лечения животных. Все это обуславливает широкое внедрение в зооинженерную и ветеринарную практику математических методов, в том числе математической статистики. Основные теоретические положения математической статистики базируются на теории вероятностей. Основное отличие математической статистики от теории вероятностей в том, что в математической статистике рассматриваются не только действия над законами распределения и числовыми характеристиками, но и приближенные методы отыскания этих законов и характеристик по результатам экспериментов. Цель данного учебно - методического пособия – помочь изучающим теорию вероятностей и математическую статистику в усвоении необходимых теоретических знаний и приобретении практических навыков для квалифицированного использования статистической информации в целях принятия правильных решений в вопросах прогнозирования.
Выборочные характеристики Средние величины Для того, чтобы количественно охарактеризовать самые существенные свойства распределения, а также для того, чтобы можно было сравнить разные распределения, вычисляют средние показатели - выборочные числовые характеристики. В статистике используются различные величины в зависимости от того, какие цели при анализе материала ставит исследователь. Понятием средней величины пользуемся в тех случаях, когда требуется определить средний надой по стаду, средний привес, средний прирост стада, средние клинические показатели деятельности сердца, лёгких, среднего состава крови и во многих других случаях. Различают следующие виды средних величин: средняя арифметическая ( Наиболее распространенным видом средних величин является средняя арифметическая, которая бывает простой и взвешенной. Возможны следующие случаи: 1. Результаты наблюдения не сведены в вариационный ряд или все частоты равны единице или одинаковы. Тогда вычисляют простую среднюю арифметическую
где хi – значение признака n – объём результатов (число наблюдений). 2. Частоты ni отличны друг от друга, то есть значения признака хi повторяются. В этом случае вычисляют среднюю арифметическую взвешенную (выборочную среднею)
3. Распределение интервальное. В этом случае вместо хi берут середину интервалов
Основные свойства среднего: 1)выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0; 2)сумма квадратов расстояний между наблюдаемыми значениями и их средним арифметическим является минимальным. Медиана выборки (термин был впервые введен Гальтоном, 1882) Медиана – это значение варианта, который делит ранжированный ряд на равные по числу вариант части. 4 7 12 8 9 5 7 13 15 Ме = 12 Ме = Свойство: сумма абсолютных расстояний между точками выборки и медианой минимальна. Если признак Х представлен интервально: медианному интервалу соответствует первая накопленная частота превосходящая n/2.
где
Модой (термин впервые введен Пирсоном,1894) называется вариант, имеющий наибольшую частоту. Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика») Мультимодальность распределения дает важную информацию о природе исследуемой переменной. Например, в социологических опросах, если переменная представляет собой предпочтения или отношение к чему-то, то мультимодальность может означать, что существует несколько определенно различных мнений. Мультимодальность так же служит индикатором того, что выборка не является однородной и наблюдения, возможно порождены двумя или более «наложенными» распределениями. Класс с наибольшей частотой называется модальным. Для определения моды интервальных рядов служит формула
где
Пример: На основании многолетних клинических наблюдений, проводившихся в Сухумском питомнике обезьян, составлена следующая выборка, включающая 100 анализов на содержание кальция (мг %) в сыворотке крови низших обезьян (павианов-гамадрилов).В данном случае признак варьирует непрерывно в пределах от 9,0 до 14,7 мг %. Задание: 1) составить интервальный вариационный ряд; 2) найти Мо, Ме; 3) построить график накопленных частот (кумуляту) Решение. 1) Установим величину классового интервала:
Определим нижнюю границу первого класса:
Составим классовые интервалы:
Получилось 8 интервалов. 2) Строим вспомогательную таблицу и разносим все 100 вариаций по намеченным классовым интервалам.
Модальный интервал 11,8-12,6, т.к. ему соответствует наибольшая частота n=25. По формуле для моды интервального вариационного ряда имеем
Медианному интервалу соответствует первая накопленная частота, превосходящая
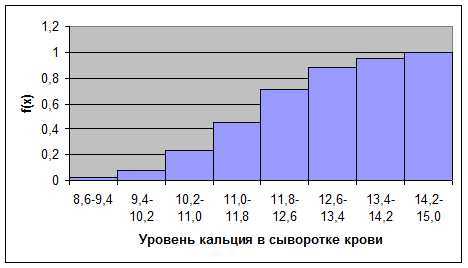
3) График накопленных частот
Степень свободы. При рассмотрении понятия дисперсии и среднего квадратического отклонения мы столкнулись с величиной n-1, которая получила особое название – число степеней свободы. В дальнейшем мы будем обозначать эту величину буквой Рассмотрим некоторый вариационный ряд, в котором имеется n вариант. При известном значении средней выборочной этого ряда каждая отдельная варианта жестко связана с остальными n – 1 вариантами. То есть в данном случае имеется n – 1 степеней свободы. Так, например, если известно, что два кролика в сумме весят 7 кг, а один из них весит 3,5 кг, то вес второго уже точно определен весом первого, то есть имеется Оценка генеральной средней. Теорема: Выборочная средняя Выборочная средняя Определение: Среднее квадратическое отклонение выборочной средней
Величину средней и её стандартную ошибку записывают так: Ошибка средней арифметической может быть выражена в относительных величинах, т.е. в %. В этом случае её называют показателем точности
Относительная ошибка выборки показывает, на сколько процентов выборочная оценка отклоняется от параметра генеральной совокупности. Чем меньше величина При выборке малого объема точечная оценка может разительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Интервальные оценки позволяют установить точность и надежность оценок. Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ. Если δ > 0 и │Θ – Θ*│< δ, то чем меньше δ, тем оценка точнее. Т.о., положительное число δ характеризует точность оценки. Однако статистические методы не позволяют категорически утверждать, что оценка Θ* удовлетворяет неравенству │Θ – Θ*│< δ; можно лишь говорить о вероятности Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность
Заменив неравенство │Θ – Θ*│< δ равносильным ему двойным неравенством
Вероятность того, что интервал (Θ* - δ; Θ* + δ) заключает в себе (покрывает) неизвестный параметр Θ, равна Доверительным интервалом называется случайный интервал (Θ*- δ; Θ*+ δ), в пределах которого с вероятностью Число Число p(или Его находят по формуле
Величина Соответственно p: 0,05; 0,01; 0,001. Очевидно, что чем меньше p, тем точнее оценка. На рис.16 показан геометрический смысл доверительной вероятности, уровня значимости и доверительного интервала. Длина доверительного интервала определяется
Рис.16 Доверительный интервал, уровень значимости Например, доверительная вероятность Определение: наибольшее отклонение Ошибка Прежде, чем перейти к интервальным оценкам параметров распределения, рассмотрим некоторые важные распределения случайной величины.
Распределение Стьюдента. В биологических исследованиях нередко приходится встречаться с выборочными совокупностями, состоящими из очень ограниченного количества вариант или наблюдений. Возникает вопрос, каковы в этих случаях закономерности распределения выборочных средних арифметических. Ответ на него дал английским математик В. Госсет, который писал под псевдонимом Стьюдент. Поэтому полученное им распределение вероятностей получило название распределения Стьюдента. Пусть то случайная переменна
распределена по закону Стьюдента с n-1 степенями свободы. Здесь
Распределение Т отличается только при малом объеме выборки. Так как В общем случае случайная величина Т определяется как
где Z – нормальная случайная величина, причем M(Z)=0, Покажем, что случайная величина (*) представляет собой частный случай случайной величины Т, распределенной по закону Стьюдента. Представим выражение (*) в следующем виде:
Величина Распределение Стьюдента зависит только от числа степеней свободы Математическое ожидание М(Т) распределения Стьюдента при Для практического использования t – распределения были составлены рабочие таблицы, по которым можно определять критические значения Замечание. Следует иметь в виду, что в случае односторонней критической области значения уровня значимости
Рис. 18. Распределение Стьюдента в зависимости от числа свободы k; сравнение со стандартизованным нормальным распределением.
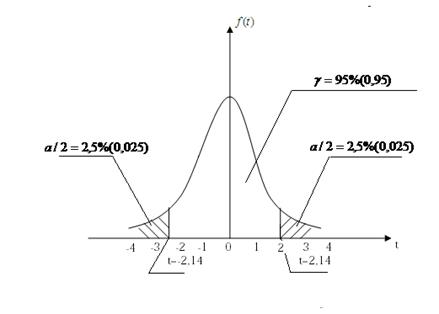
Рис. 19.95% доверительная вероятность и 5% уровень значимости для распределения Стьюдента.
Распределение Фишера. Во многих задачах математической статистики, в особенности в дисперсионном анализе, важную роль играет распределение Фишера (F-распределение), названное так по фамилии известного английского математика Р.А. Фишера (1925 г.) Если U и V независимые случайные величины, распределенные по закону
распределена по закону Фишера со степенями свободы На практике часто применяется случайная величина
Распределенная по закону Стьюдента с числом степеней свободы
Покажем, что случайная величина (**) представляет собой частный случай случайной величины (*). Перепишем (**) в виде
Случайные переменные Величина F имеет непрерывную функцию распределения и зависит только от чисел степеней свободы Наиболее часто функция F распределения табулирована для 5% (доверительная вероятность 0,95) и 1% (доверительная вероятность 0,99) уровней значимости и чисел степеней свободы
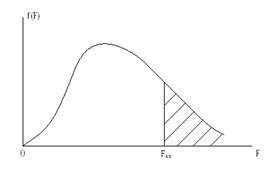
Рис. 20. Функция распределения Рис. 21. Функция распределения Фишера с односторонней Фишера с двухсторонней критической областью. критической областью.
Рассмотрим подробнее построение критических областей распределения Фишера. При использовании случайной величины F в качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий критическая область строится в зависимости от вида конкурирующей гипотезы. Первый случай: Нулевая гипотеза В этом случае строят одностороннюю, а именно правостороннюю, критическую область (рис. 20) исходя из требования, чтобы вероятность попадания величины F в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости р. Тогда правосторонняя критическая область определяется неравенством Второй случай: Нулевая гипотеза В этом случае строят двухстороннюю критическую область (рис.21) исходя из требования, чтобы вероятность попадания величины F в каждый из двух интервалов критической области, в предположении справедливости конкурирующей гипотезы, была равна Доверительные интервалы Доверительные интервалы находят по различным формулам, в зависимости от исходных данных. Уравнение прямой регрессии. Статистическую зависимость Y от X описывают с помощью уравнения вида
где Обратную статистическую зависимость можно описать уравнением регрессии X на Y:
где Функции В зависимости от вида уравнений регрессии и формы соответствующих линий регрессии говорят о различной форме статистической зависимости между изучаемыми величинами – линейной, квадратичной, показательной и т.д. Если функции
где A,B,C,D – некоторые параметры, то описываемые этими уравнениями зависимости Y от X и X от Y называются линейными; линии регрессии при этом – прямые. Если линия регрессии не является прямой, то такую зависимость называют нелинейной. Как уже было сказано выше, возможности практического применения статистической зависимости Если функции
где Угловые коэффициенты
где Из курса аналитической геометрии следует, что коэффициент линейной регрессии (угловой коэффициент линии регрессии) численно равен тангенсу угла наклона линии регрессии к соответствующей оси координат. Следовательно, чем больше, например, коэффициент
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.180 (0.014 с.) |

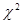 )…………………………………… 33
)…………………………………… 33 ), средняя геометрическая (
), средняя геометрическая ( ), средняя квадратическая (
), средняя квадратическая ( ), средняя гармоническая (
), средняя гармоническая ( ), мода (М0) и медиана Ме.
), мода (М0) и медиана Ме. ,
,


 ,
, - нижняя граница медианного интервала
- нижняя граница медианного интервала – шаг разбиения, ширина класса
– шаг разбиения, ширина класса – накопленная частота интервала, предшествующего медианному интервалу
– накопленная частота интервала, предшествующего медианному интервалу - абсолютная частота медианного интервала.
- абсолютная частота медианного интервала.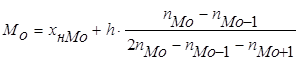 ,
, - нижняя граница модального интервала
- нижняя граница модального интервала – абсолютная частота модального интервала
– абсолютная частота модального интервала – абсолютная частота интервала, предшествующего модальному
– абсолютная частота интервала, предшествующего модальному – абсолютная частота интервала, следующего за модальным.
– абсолютная частота интервала, следующего за модальным.


 мг %
мг %





 (50).
(50).  . Следовательно, медианный интервал 11,8-12,6. По формуле для медианы интервального вариационного ряда имеем
. Следовательно, медианный интервал 11,8-12,6. По формуле для медианы интервального вариационного ряда имеем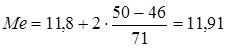
 . Объясним подробнее его значение.
. Объясним подробнее его значение.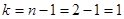 степеней свободы. Если известно, что 10 кроликов весят вместе 55 кг (т.е. выборочная средняя равна 5,5), то вес одного определяется весом девяти других, то есть имеется
степеней свободы. Если известно, что 10 кроликов весят вместе 55 кг (т.е. выборочная средняя равна 5,5), то вес одного определяется весом девяти других, то есть имеется  степеней свободы.
степеней свободы.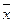 повторной выборки есть несмещённая и состоятельная оценка генеральной средней
повторной выборки есть несмещённая и состоятельная оценка генеральной средней  , причем
, причем 
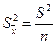 - дисперсия выборочной средней.
- дисперсия выборочной средней. называется стандартной ошибкой выборки
называется стандартной ошибкой выборки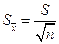 - стандартная ошибка выборки
- стандартная ошибка выборки
 и вычисляют по формуле:
и вычисляют по формуле:
 , тем достовернее, надёжнее полученная средняя. Точность средней арифметической является приемлемой, если этот коэффициент не превышает 5%.
, тем достовернее, надёжнее полученная средняя. Точность средней арифметической является приемлемой, если этот коэффициент не превышает 5%.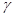 , с которой это неравенство осуществляется.
, с которой это неравенство осуществляется.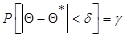



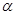 ) называется уровнем значимости и показывает, с какой вероятностью заключение о надежности оценки ошибочно.
) называется уровнем значимости и показывает, с какой вероятностью заключение о надежности оценки ошибочно. .
. % (значение доверительной вероятности, выраженной в процентах) площади под нормальной кривой выборочного распределения некоторой случайной величины. Уровень значимости
% (значение доверительной вероятности, выраженной в процентах) площади под нормальной кривой выборочного распределения некоторой случайной величины. Уровень значимости 
 , доверительная вероятность
, доверительная вероятность  для кривой нормального распределения.
для кривой нормального распределения. означает, что длина искомого доверительного интервала ограничивается 95% площади под кривой нормального распределения, т.е. полученная интервальная оценка справедлива для 95% членов генеральной совокупности. Оставшиеся 5% могут иметь отклонения от значений полученной оценки. С увеличением доверительной вероятности (уменьшением уровня значимости) увеличивается длина доверительного интервала.
означает, что длина искомого доверительного интервала ограничивается 95% площади под кривой нормального распределения, т.е. полученная интервальная оценка справедлива для 95% членов генеральной совокупности. Оставшиеся 5% могут иметь отклонения от значений полученной оценки. С увеличением доверительной вероятности (уменьшением уровня значимости) увеличивается длина доверительного интервала. оценки
оценки  от оцениваемого параметра
от оцениваемого параметра  в частности, выборочной средней (или доли) от генеральной средней (или доли), которое возможно с заданной доверительной вероятностью
в частности, выборочной средней (или доли) от генеральной средней (или доли), которое возможно с заданной доверительной вероятностью  - нормально распределенные независимые случайные величины с математическим ожиданием
- нормально распределенные независимые случайные величины с математическим ожиданием 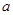 и дисперсией
и дисперсией  . Если
. Если  и
и 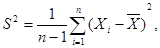
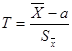 (*)
(*)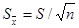 - оценка среднего квадратического отклонения выборочной средней. Легко видеть, что переменная Т принципиально сходна с формулой нормированного отклонения выборочной средней от генеральной при нормальном распределении для больших выборок:
- оценка среднего квадратического отклонения выборочной средней. Легко видеть, что переменная Т принципиально сходна с формулой нормированного отклонения выборочной средней от генеральной при нормальном распределении для больших выборок: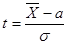
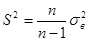 , с увеличением числа n получаем равенство
, с увеличением числа n получаем равенство 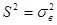 и разница между распределением Т и нормальным практически исчезает.
и разница между распределением Т и нормальным практически исчезает.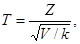 (**)
(**) а V – независимая от Z величина, которая распределена по закону
а V – независимая от Z величина, которая распределена по закону 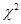 с
с 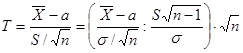
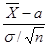 имеет нормальное распределение, величина
имеет нормальное распределение, величина 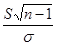 распределена по закону
распределена по закону 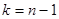 степенями свободы. Таким образом, мы получили случайную величину (**).
степенями свободы. Таким образом, мы получили случайную величину (**). практически не отличается от него. На рис. 18 на фоне нормального распределения показаны кривые распределения Стьюдента при различных степенях свободы.
практически не отличается от него. На рис. 18 на фоне нормального распределения показаны кривые распределения Стьюдента при различных степенях свободы.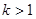 равно 0, дисперсия
равно 0, дисперсия 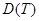 при
при  равна
равна 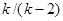 .
. , соответствующие данной доверительной вероятности
, соответствующие данной доверительной вероятности 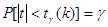 (вероятность того, что случайная величина t по абсолютной величине меньше критического значения
(вероятность того, что случайная величина t по абсолютной величине меньше критического значения 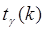 равна доверительной вероятности
равна доверительной вероятности 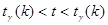 . Так, например, если выборка включает 15 наблюдений (число степеней свободы k=n-1=14) и по условиям опыта требуется доверительная вероятность 0,95 (уровень значимости 0,05), то величина t должна быть менее 2,14 и более -2,14. На рис. 19 показан графический смысл этих величин.
. Так, например, если выборка включает 15 наблюдений (число степеней свободы k=n-1=14) и по условиям опыта требуется доверительная вероятность 0,95 (уровень значимости 0,05), то величина t должна быть менее 2,14 и более -2,14. На рис. 19 показан графический смысл этих величин.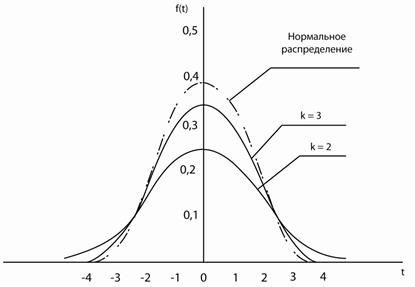
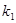 и
и  , то величина
, то величина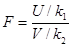 (*)
(*)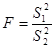
 ), (**)
), (**) (для большей дисперсии) и
(для большей дисперсии) и  (для меньшей дисперсии). Здесь
(для меньшей дисперсии). Здесь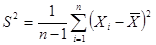 .
.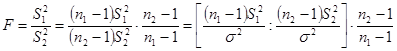 .
.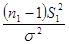 и
и 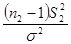 распределены по закону
распределены по закону 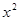 со степенями свободы
со степенями свободы 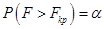 . В случае двухсторонней критической области критическим значением
. В случае двухсторонней критической области критическим значением 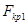 и
и 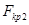 соответствует вероятности
соответствует вероятности  и
и 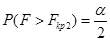 . На практике при двухсторонней критической области ограничиваются определением величины
. На практике при двухсторонней критической области ограничиваются определением величины 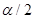 .
.
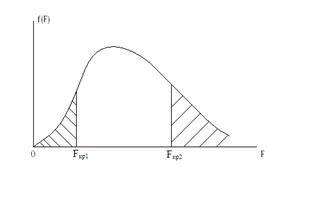
 . Конкурирующая гипотеза
. Конкурирующая гипотеза 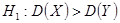 .
. . Значение
. Значение 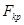 находят по заданному уровню значимости
находят по заданному уровню значимости 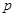 при степенях свободы
при степенях свободы  . Конкурирующая гипотеза
. Конкурирующая гипотеза 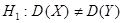 .
.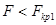 ,
,  ; область принятия нулевой гипотезы:
; область принятия нулевой гипотезы: 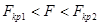 .
.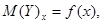
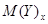 - условное математическое ожидание величины Y, соответствующее данному значению х; х – отдельные значения величины Х;
- условное математическое ожидание величины Y, соответствующее данному значению х; х – отдельные значения величины Х; 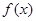 - некоторая функция. Это уравнение называется уравнением регрессии Y на Х.
- некоторая функция. Это уравнение называется уравнением регрессии Y на Х.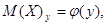
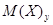 - условное математическое ожидание величины Х, соответствующее данному значению y случайной величины Y;
- условное математическое ожидание величины Х, соответствующее данному значению y случайной величины Y; 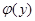 - некоторая функция.
- некоторая функция.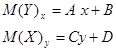 ,
,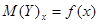 весьма ограниченны. Поэтому для характеристики формы связи между двумя случайными величинами, полученными в результате выборочных наблюдений, используют корреляционную зависимость
весьма ограниченны. Поэтому для характеристики формы связи между двумя случайными величинами, полученными в результате выборочных наблюдений, используют корреляционную зависимость 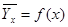 (или
(или 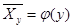 ). Уравнения, описываемые подобной зависимостью, называют выборочными уравнениями регрессии.
). Уравнения, описываемые подобной зависимостью, называют выборочными уравнениями регрессии.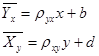 ,
,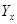 и
и 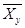 - условные средние значения величин Y и X, параметры b и d - оценки B и D,
- условные средние значения величин Y и X, параметры b и d - оценки B и D, 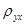 и
и 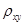 - выборочные оценки коэффициентов A и C.
- выборочные оценки коэффициентов A и C.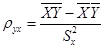 ;
; 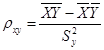 ,
,