

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Дфухфакторный дисперсионный анализ
Похожие статьи вашей тематики
В пакете Анализ данных инструмент Дфухфакторный дисперсионный анализ с повторениями представляет собой более сложный вариант двухфакторного анализа, включающего более чем одну выборку для каждой группы данных (рис. 17).
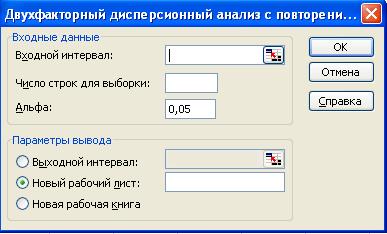
Рис. 17 Окно инструмента Дфухфакторный дисперсионный анализ с повторениями
Пример. Определить влияние пола сайгаков и топографических участков шкуры на высоту волосяного покрова (мм) (таб.2).
Алгоритм действий следующий:
1. Формируем таблицу исходных данных;
2. Сервис  Анализ данных Анализ данных  Дфухфакторный дисперсионный анализ с повторениями Дфухфакторный дисперсионный анализ с повторениями  ОК; ОК;
3. Входной интервал: А1:С11;
4. Число строк для выборки: 5;
5. Альфа: 0,05;
6. Выходной интервал: А13;
7. ОК.
Excel представит решение, показанное на рис. 18
Табл.2 Высота волосяного покрова (мм) сайгаков.
| Топографический участок (В)
| Пол (А)
| | Самка (А1)
| Самец (А2)
| | Хребет
В1
|
|
| |
|
| |
|
| |
|
| |
|
| | Огузок
В2
|
|
| |
|
| |
|
| |
|
| |
|
|
Рис. 18Результаты решения задачи с помощью инструмента Двухфакторный дисперсионный анализ с повторениями
Результаты представлены в виде двух таблиц.
1. В таблице Итоги представлены промежуточные данные расчётов для каждой строки и столбца: число элементов (Счёт), суммы величин (Сумма), среднее арифметическое величин (Среднее), дисперсия величин (Дисперсия).
2. В таблице Дисперсионный анализ представлены собственно результаты дисперсионного анализа: компоненты дисперсии (Источник вариации), суммы квадратов (SS), число степеней свободы (df), средний квадрат(MS), статистика F (F), вероятность значимости (P- значение), статистика Fкр (F критическое).
Проанализируем результаты статистической обработки.
FB<Fкрит, следовательно влияние топографического участка на высоту волосяного покрова сайгака не значимо (на 5%-ом уровне).
FА>Fкрит, следовательно пол влияет на высоту волосяного покрова сайгака.
FАВ>Fкрит, следовательно взаимодействие пола и топографического участка влияет на высоту волосяного покрова сайгака.
Подсчитаем долю влияния факторов на изменчивость признака (высота волосяного покрова) по формуле 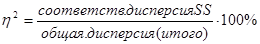
 - степень зависимости между признаком и фактором. - степень зависимости между признаком и фактором.
 - 43% вариации признака обусловлено полом сайгака. - 43% вариации признака обусловлено полом сайгака.
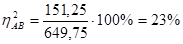 - 23% вариации признака обусловлено взаимодействием факторов. - 23% вариации признака обусловлено взаимодействием факторов.
Приложения
Приложение 1
Распределение Стьюдента (t-распределение)
|
|
| уровень значимости
| |
|
| 0,40
| 0,25
| 0,10
| 0,05
| 0,025
| 0,01
| 0,005
| | число степеней свободы
|
| 0,325
| 1,000
| 3,078
| 6,314
| 12,706
| 31,821
| 63,657
| |
| 0,289
| 0,816
| 1,886
| 2,920
| 4,303
| 6,965
| 9,925
| |
| 0,277
| 0,765
| 1,638
| 2,353
| 3,182
| 4,541
| 5,841
| |
| 0,271
| 0,741
| 1,533
| 2,132
| 2,776
| 3,747
| 4,604
| |
| 0,267
| 0,727
| 1,476
| 2,015
| 2,571
| 3,365
| 4,032
| |
| 0,265
| 0,718
| 1,440
| 1,943
| 2,447
| 3,143
| 3,707
| |
| 0,263
| 0,711
| 1,415
| 1,895
| 2,365
| 2,998
| 3,499
| |
| 0,262
| 0,706
| 1,397
| 1,860
| 2,306
| 2,896
| 3,355
| |
| 0,261
| 0,703
| 1,383
| 1,833
| 2,262
| 2,821
| 3,250
| |
| 0,260
| 0,700
| 1,372
| 1,812
| 2,228
| 2,764
| 3,169
| |
| 0,260
| 0,697
| 1,363
| 1,796
| 2,201
| 2,718
| 3,106
| |
| 0,259
| 0,695
| 1,356
| 1,782
| 2,179
| 2,681
| 3,055
| |
| 0,259
| 0,694
| 1,350
| 1,771
| 2,160
| 2,650
| 3,012
| |
| 0,258
| 0,692
| 1,345
| 1,761
| 2,145
| 2,624
| 2,977
| |
| 0,258
| 0,691
| 1,341
| 1,753
| 2,131
| 2,602
| 2,947
| |
| 0,258
| 0,690
| 1,337
| 1,746
| 2,120
| 2,583
| 2,921
| |
| 0,257
| 0,689
| 1,333
| 1,740
| 2,110
| 2,567
| 2,898
| |
| 0,257
| 0,688
| 1,330
| 1,734
| 2,101
| 2,552
| 2,878
| |
| 0,257
| 0,688
| 1,328
| 1,729
| 2,093
| 2,539
| 2,861
| |
| 0,257
| 0,687
| 1,325
| 1,725
| 2,086
| 2,528
| 2,845
| |
| 0,257
| 0,686
| 1,323
| 1,721
| 2,080
| 2,518
| 2,831
| |
| 0,256
| 0,686
| 1,321
| 1,717
| 2,074
| 2,508
| 2,819
| |
| 0,256
| 0,685
| 1,319
| 1,714
| 2,069
| 2,500
| 2,807
| |
| 0,256
| 0,685
| 1,318
| 1,711
| 2,064
| 2,492
| 2,797
| |
| 0,256
| 0,684
| 1,316
| 1,708
| 2,060
| 2,485
| 2,787
| |
| 0,256
| 0,684
| 1,315
| 1,706
| 2,056
| 2,479
| 2,779
| |
| 0,256
| 0,684
| 1,314
| 1,703
| 2,052
| 2,473
| 2,771
| |
| 0,256
| 0,683
| 1,313
| 1,701
| 2,048
| 2,467
| 2,763
| |
| 0,256
| 0,683
| 1,311
| 1,699
| 2,045
| 2,462
| 2,756
| |
| 0,256
| 0,683
| 1,310
| 1,697
| 2,042
| 2,457
| 2,750
| |
| 0,255
| 0,681
| 1,303
| 1,684
| 2,021
| 2,423
| 2,704
| |
| 0,255
| 0,680
| 1,296
| 1,676
| 2,009
| 2,403
| 2,678
| |
| 0,255
| 0,679
| 1,296
| 1,671
| 2,000
| 2,390
| 2,660
| |
| 0,254
| 0,679
| 1,292
| 1,664
| 1,990
| 2,374
| 2,639
| |
| 0,254
| 0,678
| 1,290
| 1,660
| 1,984
| 2,365
| 2,626
| |
| 0,254
| 0,677
| 1,289
| 1,658
| 1,980
| 2,358
| 2,467
| |
| 0,254
| 0,676
| 1,286
| 1,653
| 1,972
| 2,345
| 2,601
|
 Приложение 2 Приложение 2
Распределение Фишера (F-распределение)

| число степеней свободы v1
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | число степеней свободы v 2
|
| 39,86
| 49,50
| 53,59
| 55,83
| 57,24
| 58,20
| 58,91
| 59,44
| 59,86
| 60,19
| 60,50
| 60,71
| 61,22
| 61,74
| 62,00
| 62,26
| 62,53
| 62,79
| 63,06
| |
| 8,53
| 9,00
| 9,16
| 9,24
| 9,29
| 9,33
| 9,35
| 9,37
| 9,38
| 9,39
| 9,40
| 9,41
| 9,42
| 9,44
| 9,45
| 9,46
| 9,47
| 9,47
| 9,48
| |
| 5,54
| 5,46
| 5,39
| 5,34
| 5,31
| 5,28
| 5,27
| 5,25
| 5,24
| 5,23
| 5,22
| 5,22
| 5,20
| 5,18
| 5,18
| 5,17
| 5,16
| 5,15
| 5,14
| |
| 4,54
| 4,32
| 4,19
| 4,11
| 4,05
| 4,01
| 3,98
| 3,95
| 3,94
| 3,92
| 3,91
| 3,90
| 3,87
| 3,84
| 3,83
| 3,82
| 3,80
| 3,79
| 3,78
| |
| 4,06
| 3,78
| 3,62
| 3,52
| 3,45
| 3,40
| 3,37
| 3,34
| 3,32
| 3,30
| 3,28
| 3,27
| 3,24
| 3,21
| 3,19
| 3,17
| 3,16
| 3,14
| 3,12
| |
| 3,78
| 3,46
| 3,29
| 3,18
| 3,11
| 3,05
| 3,01
| 2,98
| 2,96
| 2,94
| 2,92
| 2,90
| 2,87
| 2,84
| 2,82
| 2,80
| 2,78
| 2,76
| 2,74
| |
| 3,59
| 3,26
| 3,07
| 2,96
| 2,88
| 2,83
| 2,78
| 2,75
| 2,72
| 2,70
| 2,68
| 2,67
| 2,63
| 2,59
| 2,58
| 2,56
| 2,54
| 2,51
| 2,49
| |
| 3,46
| 3,11
| 2,92
| 2,81
| 2,73
| 2,67
| 2,62
| 2,59
| 2,56
| 2,54
| 2,52
| 2,50
| 2,46
| 2,42
| 2,40
| 2,38
| 2,36
| 2,34
| 2,32
| |
| 3,36
| 3,01
| 2,81
| 2,69
| 2,61
| 2,55
| 2,51
| 2,47
| 2,44
| 2,42
| 2,40
| 2,38
| 2,34
| 2,30
| 2,28
| 2,25
| 2,23
| 2,21
| 2,18
| |
| 3,29
| 2,92
| 2,73
| 2,61
| 2,52
| 2,46
| 2,41
| 2,38
| 2,35
| 2,32
| 2,30
| 2,28
| 2,24
| 2,20
| 2,18
| 2,16
| 2,13
| 2,11
| 2,08
| |
| 3,23
| 2,86
| 2,66
| 2,54
| 2,45
| 2,39
| 2,34
| 2,30
| 2,27
| 2,25
| 2,23
| 2,21
| 2,17
| 2,12
| 2,10
| 2,08
| 2,05
| 2,03
| 2,00
| |
| 3,18
| 2,81
| 2,61
| 2,48
| 2,39
| 2,33
| 2,28
| 2,24
| 2,21
| 2,19
| 2,17
| 2,15
| 2,10
| 2,06
| 2,04
| 2,01
| 1,99
| 1,96
| 1,93
| |
| 3,14
| 2,76
| 2,56
| 2,43
| 2,35
| 2,28
| 2,23
| 2,20
| 2,16
| 2,14
| 2,12
| 2,10
| 2,05
| 2,01
| 1,98
| 1,96
| 1,93
| 1,90
| 1,88
| |
| 3,10
| 2,73
| 2,52
| 2,39
| 2,31
| 2,24
| 2,19
| 2,15
| 2,12
| 2,10
| 2,08
| 2,05
| 2,01
| 1,96
| 1,94
| 1,91
| 1,89
| 1,86
| 1,83
| |
| 3,07
| 2,70
| 2,49
| 2,36
| 2,27
| 2,21
| 2,16
| 2,12
| 2,09
| 2,06
| 2,04
| 2,02
| 1,97
| 1,92
| 1,90
| 1,87
| 1,85
| 1,82
| 1,79
| |
| 3,05
| 2,67
| 2,46
| 2,33
| 2,24
| 2,18
| 2,13
| 2,09
| 2,06
| 2,03
| 2,01
| 1,99
| 1,94
| 1,89
| 1,87
| 1,84
| 1,81
| 1,78
| 1,75
| |
| 3,03
| 2,64
| 2,44
| 2,31
| 2,22
| 2,15
| 2,10
| 2,06
| 2,03
| 2,00
| 1,98
| 1,96
| 1,91
| 1,86
| 1,84
| 1,81
| 1,78
| 1,75
| 1,72
| |
| 3,01
| 2,62
| 2,42
| 2,29
| 2,20
| 2,13
| 2,08
| 2,04
| 2,00
| 1,98
| 1,96
| 1,93
| 1,89
| 1,84
| 1,81
| 1,78
| 1,75
| 1,72
| 1,69
| |
| 2,99
| 2,61
| 2,40
| 2,27
| 2,18
| 2,11
| 2,06
| 2,02
| 1,98
| 1,96
| 1,94
| 1,91
| 1,86
| 1,81
| 1,79
| 1,76
| 1,73
| 1,70
| 1,67
| |
| 2,97
| 2,59
| 2,38
| 2,25
| 2,16
| 2,09
| 2,04
| 2,00
| 1,96
| 1,94
| 1,92
| 1,89
| 1,84
| 1,79
| 1,77
| 1,74
| 1,71
| 1,68
| 1,64
| |
| 2,95
| 2,56
| 2,35
| 2,22
| 2,13
| 2,06
| 2,01
| 1,97
| 1,93
| 1,90
| 1,88
| 1,86
| 1,81
| 1,76
| 1,73
| 1,70
| 1,67
| 1,64
| 1,60
| |
| 2,93
| 2,54
| 2,33
| 2,19
| 2,10
| 2,04
| 1,98
| 1,94
| 1,91
| 1,88
| 1,85
| 1,83
| 1,78
| 1,73
| 1,70
| 1,67
| 1,64
| 1,61
| 1,57
| |
| 2,91
| 2,52
| 2,31
| 2,17
| 2,08
| 2,01
| 1,96
| 1,92
| 1,88
| 1,86
| 1,84
| 1,81
| 1,76
| 1,71
| 1,68
| 1,65
| 1,61
| 1,58
| 1,54
| |
| 2,89
| 2,50
| 2,29
| 2,16
| 2,06
| 2,00
| 1,94
| 1,90
| 1,87
| 1,84
| 1,81
| 1,79
| 1,74
| 1,69
| 1,66
| 1,63
| 1,59
| 1,56
| 1,52
| |
| 2,88
| 2,49
| 2,28
| 2,14
| 2,05
| 1,98
| 1,93
| 1,88
| 1,85
| 1,82
| 1,79
| 1,77
| 1,72
| 1,67
| 1,64
| 1,61
| 1,57
| 1,54
| 1,50
| |
| 2,84
| 2,44
| 2,23
| 2,09
| 2,00
| 1,93
| 1,87
| 1,83
| 1,79
| 1,76
| 1,73
| 1,71
| 1,66
| 1,61
| 1,57
| 1,54
| 1,51
| 1,47
| 1,42
| |
| 2,79
| 2,39
| 2,18
| 2,04
| 1,95
| 1,87
| 1,82
| 1,77
| 1,74
| 1,71
| 1,68
| 1,66
| 1,60
| 1,54
| 1,51
| 1,48
| 1,44
| 1,40
| 1,35
| |
| 2,75
| 2,35
| 2,13
| 1,99
| 1,90
| 1,82
| 1,77
| 1,72
| 1,68
| 1,65
| 1,62
| 1,60
| 1,55
| 1,48
| 1,45
| 1,41
| 1,37
| 1,32
| 1,26
|
 Приложение 2 (продолжение) Приложение 2 (продолжение)
Распределение Фишера (F-распределение)

| число степеней свободы v1
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | число степеней свободы v 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 18,5
| 19,0
| 19,2
| 19,2
| 19,3
| 19,3
| 19,4
| 19,4
| 19,4
| 19,4
| 19,4
| 19,4
| 19,4
| 19,4
| 19,5
| 19,5
| 19,5
| 19,5
| 19,5
| |
| 10,1
| 9,55
| 9,28
| 9,12
| 9,01
| 8,94
| 8,89
| 8,85
| 8,81
| 8,79
| 8,76
| 8,74
| 8,70
| 8,66
| 8,64
| 8,62
| 8,59
| 8,57
| 8,55
| |
| 7,71
| 6,94
| 6,59
| 6,39
| 6,26
| 6,16
| 6,09
| 6,04
| 6,00
| 5,96
| 5,94
| 5,91
| 5,86
| 5,80
| 5,77
| 5,75
| 5,72
| 5,69
| 5,66
| |
| 6,61
| 5,79
| 5,41
| 5,19
| 5,05
| 4,95
| 4,88
| 4,82
| 4,77
| 4,74
| 4,71
| 4,68
| 4,62
| 4,56
| 4,53
| 4,50
| 4,46
| 4,43
| 4,40
| |
| 5,99
| 5,14
| 4,76
| 4,53
| 4,39
| 4,28
| 4,21
| 4,15
| 4,10
| 4,06
| 4,03
| 4,00
| 3,94
| 3,87
| 3,84
| 3,81
| 3,77
| 3,74
| 3,70
| |
| 5,59
| 4,74
| 4,35
| 4,12
| 3,97
| 3,87
| 3,79
| 3,73
| 3,68
| 3,64
| 3,60
| 3,57
| 3,51
| 3,44
| 3,41
| 3,38
| 3,34
| 3,30
| 3,27
| |
| 5,32
| 4,46
| 4,07
| 3,84
| 3,69
| 3,58
| 3,50
| 3,44
| 3,39
| 3,35
| 3,31
| 3,28
| 3,22
| 3,15
| 3,12
| 3,08
| 3,04
| 3,01
| 2,97
| |
| 5,12
| 4,26
| 3,86
| 3,63
| 3,48
| 3,37
| 3,29
| 3,23
| 3,18
| 3,14
| 3,10
| 3,07
| 3,01
| 2,94
| 2,90
| 2,86
| 2,83
| 2,79
| 2,75
| |
| 4,96
| 4,10
| 3,71
| 3,48
| 3,33
| 3,22
| 3,14
| 3,07
| 3,02
| 2,98
| 2,94
| 2,91
| 2,85
| 2,77
| 2,74
| 2,70
| 2,66
| 2,62
| 2,58
| |
| 4,84
| 3,98
| 3,59
| 3,36
| 3,20
| 3,09
| 3,01
| 2,95
| 2,90
| 2,85
| 2,82
| 2,79
| 2,72
| 2,65
| 2,61
| 2,57
| 2,53
| 2,49
| 2,45
| |
| 4,75
| 3,89
| 3,49
| 3,26
| 3,11
| 3,00
| 2,91
| 2,85
| 2,80
| 2,75
| 2,72
| 2,69
| 2,62
| 2,54
| 2,51
| 2,47
| 2,43
| 2,38
| 2,34
| |
| 4,67
| 3,81
| 3,41
| 3,18
| 3,03
| 2,92
| 2,83
| 2,77
| 2,71
| 2,67
| 2,63
| 2,60
| 2,53
| 2,46
| 2,42
| 2,38
| 2,34
| 2,30
| 2,25
| |
| 4,60
| 3,74
| 3,34
| 3,11
| 2,96
| 2,85
| 2,76
| 2,70
| 2,65
| 2,60
| 2,57
| 2,53
| 2,46
| 2,39
| 2,35
| 2,31
| 2,27
| 2,22
| 2,18
| |
| 4,54
| 3,68
| 3,29
| 3,06
| 2,90
| 2,79
| 2,71
| 2,64
| 2,59
| 2,54
| 2,51
| 2,48
| 3,52
| 3,37
| 3,29
| 3,21
| 3,13
| 3,05
| 2,96
| |
| 4,49
| 3,63
| 3,24
| 3,01
| 2,85
| 2,74
| 2,66
| 2,59
| 2,54
| 2,49
| 2,46
| 2,42
| 2,35
| 2,28
| 2,24
| 2,19
| 2,15
| 2,11
| 2,06
| |
| 4,45
| 3,59
| 3,20
| 2,96
| 2,81
| 2,70
| 2,61
| 2,55
| 2,49
| 2,45
| 2,41
| 2,38
| 2,31
| 2,23
| 2,19
| 2,15
| 2,10
| 2,06
| 2,01
| |
| 4,41
| 3,55
| 3,16
| 2,93
| 2,77
| 2,66
| 2,58
| 2,51
| 2,46
| 2,41
| 2,37
| 2,34
| 2,27
| 2,19
| 2,15
| 2,11
| 2,06
| 2,02
| 1,97
| |
| 4,38
| 3,52
| 3,13
| 2,90
| 2,74
| 2,63
| 2,54
| 2,48
| 2,42
| 2,38
| 2,34
| 2,31
| 2,23
| 2,16
| 2,11
| 2,07
| 2,03
| 1,98
| 1,93
| |
| 4,35
| 3,49
| 3,10
| 2,87
| 2,71
| 2,60
| 2,51
| 2,45
| 2,39
| 2,35
| 2,31
| 2,28
| 2,20
| 2,12
| 2,08
| 2,04
| 1,99
| 1,95
| 1,90
| |
| 4,30
| 3,44
| 3,05
| 2,82
| 2,66
| 2,55
| 2,46
| 2,40
| 2,34
| 2,30
| 2,26
| 2,23
| 2,15
| 2,07
| 2,03
| 1,98
| 1,94
| 1,89
| 1,84
| |
| 4,26
| 3,40
| 3,01
| 2,78
| 2,62
| 2,51
| 2,42
| 2,36
| 2,30
| 2,25
| 2,21
| 2,18
| 2,11
| 2,03
| 1,98
| 1,94
| 1,89
| 1,84
| 1,79
| |
| 4,23
| 3,37
| 2,98
| 2,74
| 2,59
| 2,47
| 2,39
| 2,32
| 2,27
| 2,22
| 2,18
| 2,15
| 2,07
| 1,99
| 1,95
| 1,90
| 1,85
| 1,80
| 1,75
| |
| 4,20
| 3,34
| 2,95
| 2,71
| 2,56
| 2,45
| 2,36
| 2,29
| 2,24
| 2,19
| 2,15
| 2,12
| 2,04
| 1,96
| 1,91
| 1,87
| 1,82
| 1,77
| 1,71
| |
| 4,17
| 3,32
| 2,92
| 2,69
| 2,53
| 2,42
| 2,33
| 2,27
| 2,21
| 2,16
| 2,13
| 2,09
| 2,01
| 1,93
| 1,89
| 1,84
| 1,79
| 1,74
| 1,68
| |
| 4,08
| 3,23
| 2,84
| 2,61
| 2,45
| 2,34
| 2,25
| 2,18
| 2,12
| 2,08
| 2,04
| 2,00
| 1,92
| 1,84
| 1,79
| 1,74
| 1,69
| 1,64
| 1,58
| |
| 4,00
| 3,15
| 2,76
| 2,53
| 2,37
| 2,25
| 2,17
| 2,10
| 2,04
| 1,99
| 1,95
| 1,92
| 1,84
| 1,75
| 1,70
| 1,65
| 1,59
| 1,53
| 1,47
| |
| 3,92
| 3,07
| 2,68
| 2,45
| 2,29
| 2,17
| 2,09
| 2,02
| 1,96
| 1,91
| 1,87
| 1,83
| 1,75
| 1,66
| 1,61
| 1,55
| 1,50
| 1,43
| 1,35
|
Приложение 3
Таблица значений функции Лапласа
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
| | 0.00
| 0.0000
| 0.32
| 0.1255
| 0.64
| 0.2389
| 0.96
| 0.3315
| | 0.01
| 0.0040
| 0.33
| 0.1293
| 0.65
| 0.2422
| 0.97
| 0.3340
| | 0.02
| 0.0080
| 0.34
| 0.1331
| 0.66
| 0.2454
| 0.98
| 0.3365
| | 0.03
| 0.0120
| 0.35
| 0.1368
| 0.67
| 0.2486
| 0.99
| 0.3389
| | 0.04
| 0.0160
| 0.36
| 0.1406
| 0.68
| 0.2517
| 1.00
| 0.3413
| | 0.05
| 0.0199
| 0.37
| 0.1443
| 0.69
| 0.2549
| 1.01
| 0.3438
| | 0.06
| 0.0239
| 0.38
| 0.1480
| 0.70
| 0.2580
| 1.02
| 0.3461
| | 0.07
| 0.0279
| 0.39
| 0.1517
| 0.71
| 0.2611
| 1.03
| 0.3485
| | 0.08
| 0.0319
| 0.40
| 0.1554
| 0.72
| 0.2642
| 1.04
| 0.3508
| | 0.09
| 0.0359
| 0.41
| 0.1591
| 0.73
| 0.2673
| 1.05
| 0.3531
| | 0.10
| 0.0398
| 0.42
| 0.1628
| 0.74
| 0.2703
| 1.06
| 0.3554
| | 0.11
| 0.0438
| 0.43
| 0.1664
| 0.75
| 0.2734
| 1.07
| 0.3577
| | 0.12
| 0.0478
| 0.44
| 0.1700
| 0.76
| 0.2764
| 1.08
| 0.3599
| | 0.13
| 0.0517
| 0.45
| 0.1736
| 0.77
| 0.2794
| 1.09
| 0.3621
| | 0.14
| 0.0557
| 0.46
| 0.1772
| 0.78
| 0.2823
| 1.10
| 0.3643
| | 0.15
| 0.0596
| 0.47
| 0.1808
| 0.79
| 0.2852
| 1.11
| 0.3665
| | 0.16
| 0.0636
| 0.48
| 0.1844
| 0.80
| 0.2881
| 1.12
| 0.3686
| | 0.17
| 0.0675
| 0.49
| 0.1879
| 0.81
| 0.2910
| 1.13
| 0.3708.
| | 0.18
| 0.0714
| 0.50
| 0.1915
| 0.82
| 0.2939
| 1.14
| 0.3729
| | 0.19
| 0.0753
| 0.51
| 0.1950
| 0.83
| 0.2967
| 1.15
| 0.3749
| | 0.20
| 0.0793
| 0.52
| 0.1985
| 0.84
| 0.2995
| 1.16
| 0.3770
| | 0.21
| 0.0832
| 0.53
| 0.2019
| 0.85
| 0.3023
| 1.17
| 0.3790
| | 0.22
| 0.0871
| 0.54
| 0.2054
| 0.86
| 0.3051
| 1.18
| 0.3810
| | 0.23
| 0.0910
| 0.55
| 0.2088
| 0.87
| 0.3078
| 1.19
| 0.3830
| | 0.24
| 0.0948
| 0.56
| 0.2123
| 0.88
| 0.3106
| 1.20
| 0.3849
| | 0.25
| 0.0987
| 0.57
| 0.2157
| 0.89
| 0.3133
| 1.21
| 0.3869
| | 0.26
| 0.1026
| 0.58
| 0.2190
| 0.90
| 0.3159
| 1.22
| 0/3883
| | 0.27
| 0.1064
| 0.59
| 0.2224
| 0.91
| 0.3186
| 1.23
| 0.3907
| | 0.28
| 0.1103
| 0.60
| 0.2257
| 0.92
| 0.3212
| 1.24
| 0.3925
| | 0.29
| 0.1141
| 0.61
| 0.2291
| 0.93
| 0.3238
| 1.25
| 0.3944
| | 0.30
| 0.1179
| 0.62
| 0.2324
| 0.94
| 0.3264
|
|
| | 0.31
| 0.1217
| 0.63
| 0.2357
| 0.95
| 0.3289
|
|
|
Продолжение приложения 3
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
| | 1.26
| 0.3962
| 1.59
| 0.4441
| 1.92
| 0.4726
| 2.50
| 0.4938
| | 1.27
| 0.3980
| 1.60
| 0.4452
| 1.93
| 0.4732
| 2.52
| 0.4941
| | 1.28
| 0.3997
| 1.61
| 0.4463
| 1.94
| 0.4738
| 2.54
| 0.4945
| | 1.29
| 0.4015
| 1.62
| 0.4474
| 1.95
| 0.4744
| 2.56
| 0.4948
| | 1.30
| 0.4032
| 1.63
| 0.4484
| 1.96
| 0.4750
| 2.58
| 0.4951
| | 1.31
| 0.4049
| 1.64
| 0.4495
| 1.97
| 0.4756
| 2.60
| 0.4953
| | 1.32
| 0.4066
| 1.65
| 0.4505
| 1.98
| 0.4761
| 2.62
| 0.4956
| | 1.33
| 0.4082
| 1.66
| 0.4515
| 1.99
| 0.4767
| 2.64
| 0.4959
| | 1.34
| 0.4099
| 1.67
| 0.4525
| 2.00
| 0.4772
| 2.66
| 0.4961
| | 1.35
| 0.4115
| 1.68
| 0.4535
| 2.02
| 0.4783
| 2.68
| 0.4963
| | 1.36
| 0.4131
| 1.69
| 0.4545
| 2.04
| 0.4793
| 2.70
| 0.4965
| | 1.37
| 0.4147
| 1.70
| 0.4554
| 2.06
| 0.4803
| 2.72
| 0.4967
| | 1.38
| 0.4162
| 1.71
| 0.4564
| 2.08
| 0.4812
| -2.74
| 0.4969
| | 1.39
| 0.4177
| 1.72
| 0.4573
| 2.10
| 0.4821
| 2.76
| 0.4971
| | 1.40
| 0.4192
| 1.73
| 0.4582
| 2.12
| 0.4830
| 2.78
| 0.4973
| | 1.41
| 0.4207
| 1.74
| 0.4591
| 2.14
| 0.4838
| 2.80
| 0.4974
| | 1.42
| 0.4222
| 1.75
| 0.4599
| 2.16
| 0.4846
| 2.82
| 0.4976
| | 1.43
| 0.4236
| 1.76
| 0.4608
| 2.18
| 0.4854
| 2.84
| 0.4977
| | 1.44
| 0.4251
| 1.77
| 0.4616
| 2.20
| 0.4861
| 2.86
| 0.4979
| | 1.45
| 0.4265
| 1.78
| 0.4625
| 2.22
| 0.4868
| 2.88
| 0.4980
| | 1.46
| 0.4279
| 1.79
| 0.4633
| 2.24
| 0.4875
| 2.90
| 0.4981
| | 1.47
| 0.4292
| 1.80
| 0.4641
| 2.26
| 0.4881
| 2.92
| 0.4982
| | 1.48
| 0.4306
| 1.81
| 0.4649
| 2.28
| 0.4887
| 2.94
| 0.4984
| | 1.49
| 0.4319
| 1.82
| 0.4656
| 2.30
| 0.4893
| 2.96
| 0.4985
| | 1.50
| 0.4332
| 1.83
| 0.4664
| 2.32
| 0.4898
| 2.98
| 0.4986
| | 1.51
| 0.4345
| 1.84
| 0.4671
| 2.34
| 0.4904
| 3.00
| 0.49865
| | 1.52
| 0.4357
| 1.85
| 0.4678
| 2.36
| 0.4909
| 3.20
| 0.49931
| | 1.53
| 0.4370
| 1.86
| 0.4686
| 2.38
| 0.4913
| 3.40
| 0.49966
| | 1.54
| 0.4382
| 1.87
| 0.4693
| 2.40
| 0.4918
| 3.60
| 0.49984
| | 1.55
| 0.4394
| 1.88
| 0.4699
| 2.42
| 0.4922
| 3.80
| 0.49992
| | 1.56
| 0.4406
| 1.89
| 0.4706
| 2.44
| 0.4927
| 4.00
| 0.49996
| | 1.57
| 0.4418
| 1.90
| 0.4713
| 2.46
| 0.4931
| 4.50
| 0.49999
| | 1.58
| 0.4429
| 1 1.91
| 0.4719
| 2.48
| 0.4934
| S 5.00
| 0.49999
|
 Приложение 4 Приложение 4
Критические точки распределения 
| Число степеней свободы
k
| Уровень значимости a
| | 0,01
| 0,025
| 0.05
| 0,95
| 0,975
| 0.99
| |
| 6.6
| 5.0
| 3.8
| 0.0039
| 0.00098
| 0.00016
| |
| 9.2
| 7.4
| 6.0
| 0.103
| 0.051
| 0.020
| |
| 11.3
| 9.4
| 7.8
| 0.352
| 0.216
| 0.115
| |
| 13.3
| 11.1
| 9.5
| 0.711
| 0.484
| 0.297
| |
| 15.1
| 12.8
| 11.1
| 1.15
| 0.831
| 0.554
| |
| 16.8
| 14.4
| 12.6
| 1.64
| 1.24
| 0.872
| |
| 18.5
| 16.0
| 14.1
| 2.17
| 1.69
| 1.24
| |
| 20.1
| 17.5
| 15.5
| 2.73
| 2.18
| 1.65
| |
| 21.7
| 19.0
| 16.9
| 3.33
| 2.70
| 2.09
| |
| 23.2
| 20.5
| 18.3
| 3.94
| 3.25
| 2.56
| |
| 24.7
| 21.9
| 19.7
| 4.57
| 3.82
| 3.05
| |
| 26.2
| 23.3
| 21.0
| 5.23
| 4.40
| 3.57
| |
| 27.7
| 24.7
| 22.4
| 5.89
| 5.01
| 4.11
| |
| 29.1
| 26.1
| 23.7
| 6.57
| 5.63
| 4.66
| |
| 30.6
| 27.5
| 25.0
| 7.26
| 6.26
| 5.23
| |
| 32.0
| 28.8
| 26.3
| 7.96
| 6.91
| 5.81
| |
| 33.4
| 30.2
| 27.6
| 8.67
| 7.56
| 6.41
| |
| 34.8
| 31.5
| 28.9
| 9.39
| 8.23
| 7.01
| |
| 36.2
| 32.9
| 30.1
| 10.1
| 8.91
| 7.63
| |
| 37.6
| 34.2
| 31.4
| 10.9
| 9.59
| 8.26
| |
| 38.9
| 35.5
| 32.7
| 11.6
| 10.3
| 8.90
| |
| 40.3
| 36.8
| 33.9
| 12.3
| 11.0
| 9.54
| |
| 41.6
| 38.1
| 35.2
| 13.1
| 11.7
| 10.2
| |
| 43.0
| 39.4
| 36.4
| 13.8
| 12.4
| 10.9
| |
| 44.3
| 40.6
| 37.7
| 14.6
| 13.1
| 11.5
| |
| 45.6
| 41.9
| 38.9
| 15.4
| 13.8
| 12.2
| |
| 47.0
| 43.2
| 40.1
| 16.2
| 14.6
| 12.9
| |
| 48.3
| 44.5
| 41.3
| 16.9
| 15.3
| 13.6
| |
| 49.6
| 45.7
| 42.6
| 17.7
| 16.0
| 14.3
| |
| 50.9
| 47.0
| 43.8
| 18.5
| 16.8
| 15.0
|
 Приложение 5 Приложение 5
Критические точки распределения Стьюдента
| Число степеней свободы
k
| Уровень значимости a (двусторонняя критическая область)
| |
0.10
|
0.05
|
0.02
|
0.01
|
0.002
|
0.001
| |
| 6.31
| 12.7
| 31.82
| 63.7
| 318.3
| 637.0
| |
| 2.92
| 4.30
| 6.97
| 9.92
| 22.33
| 31.6
| |
| 2.35
| 3.18
| 4.54
| 5.84
| 10.22
| 12.9
| |
| 2.13
| 2.78
| 3.75
| 4.60
| 7.17
| 8.61
| |
| 2.01
| 2.57
| 3.37
| 4.03
| 5.89
| 6.86
| |
| 1.94
| 2.45
| 3.14
| 3.71
| 5.21
| 5.96
| |
| 1.89
| 2.36
| 3.00
| 3.50
| 4.79
| 5.40
| |
| 1.86
| 2.31
| 2.90
| 3.36
| 4.50
| 5.04
| |
| 1.83
| 2.26
| 2.82
| 3.25
| 4.30
| 4.78
| |
| 1.81
| 2.23
| 2.76
| 3.17
| 4.14
| 4.59
| |
| 1.80
| 2.20
| 2.72
| 3.11
| 4.03
| 4.44
| |
| 1.78
| 2.18
| 2.68
| 3.05
| 3.93
| 4.32
| |
| 1.77
| 2.16
| 2.65
| 3.01
| 3.85
| 4.22
| |
| 1.76
| 2.14
| 2.62
| 2.98
| 3.79
| 4.14
| |
| 1.75
| 2.13
| 2.60
| 2.95
| 3.73
| 4.07
| |
| 1.75
| 2.12
| 2.58
| 2.92
| 3.69
| 4.01
| |
| 1.74
| 2.11
| 2.57
| 2.90
| 3.65
| 3.95
| |
| 1.73
| 2.10
| 2.55
| 2.88
| 3.61
| 3.92
| |
| 1.73
| 2.09
| 2.54
| 2.86
| 3.58
| 3.88
| |
| 1.73
| 2.09
| 2.53
| 2.85
| 3.55
| 3.85
| |
| 1.72
| 2.08
| 2.52
| 2.83
| 3.53
| 3.82
| |
| 1.72
| 2.07
| 2.51
| 2.82
| 3.51
| 3.79
| |
| 1.71
| 2.07
| 2.50
| 2.81
| 3.59
| 3.77
| |
| 1.71
| 2.06
| 2.49
| 2.80
| 3.47
| 3.74
| |
| 1.71
| 2.06
| 2.49
| 2.79
| 3.45
| 3.72
| |
| 1.71
| 2.06
| 2.48
| 2.78
| 3.44
| 3.71
| |
| 1.71
| 2.05
| 2.47
| 2.77
| 3.42
| 3.69
| |
| 1.70
| 2.05
| 2.46
| 2.76
| 3.40
| 3.66
| |
| 1.70
| 2.05
| 2.46
| 2.76
| 3.40
| 3.66
| |
| 1.70
| 2.04
| 2.46
| 2.75
| 3.39
| 3.65
| |
| 1.68
| 2.02
| 2.42
| 2.70
| 3.31
| 3.55
| |
| 1.67
| 2.00
| 2.39
| 2.66
| 3.23
| 3.46
| |
| 1.66
| 1.98
| 2.36
| 2.62
| 3.17
| 3.37
| | ¥
| 1.64
| 1.96
| 2.33
| 2.58
| 3.09
| 3.29
| |
| 0.05
| 0.025
| 0.01
| 0.005
| 0.001
| 0.0005
| |
| Уровень значимости a
(односторонняя критическая область)
|
 Приложение 6 Приложение 6
Критические точки распределения Фишера
(  |




 Анализ данных
Анализ данных 
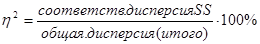
 - степень зависимости между признаком и фактором.
- степень зависимости между признаком и фактором. - 43% вариации признака обусловлено полом сайгака.
- 43% вариации признака обусловлено полом сайгака.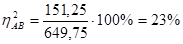 - 23% вариации признака обусловлено взаимодействием факторов.
- 23% вариации признака обусловлено взаимодействием факторов. Приложение 2
Приложение 2
 Приложение 2 (продолжение)
Приложение 2 (продолжение)





