
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсионный анализ данных однофакторного полевогоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опыта
Цель занятия: 1.Ознакомиться с сущностью и основными понятиями дисперсионного анализа. 2. Освоить проведение дисперсионного анализа данных однофакторного полевого опыта, проведенного методом организованных повторений. 3. Освоить методику проверки нулевой гипотезы и составления выводов по результатам дисперсионного анализа.
Сущностью дисперсионного анализа является разделение общей суммы квадратов отклонений (Су) и общего числа степеней свободы (N-1) на части – компоненты, соответствующие структуре эксперимента, и оценка значимости действия и взаимодействия изучаемых факторов по F-критерию. Основной задачей дисперсионного анализа является определение доли или степени влияния различных факторов (вариант, повторение, ошибка) в отдельности и суммарного их воздействия на изменчивость результативного признака. При дисперсионном анализе одновременно обрабатывают данные нескольких вариантов (выборок) опыта по повторениям. Схема дисперсионного анализа определяется числом изучаемых факторов и методом размещения вариантов. Если обрабатывают однофакторные опыты, состоящие из нескольких, например, l -вариантов в вегетационном опыте или при размещении вариантов в полевом опыте методом полной рендомизации, то общая изменчивость результативного признака, измеряемая общей суммой квадратов (Су), расчленяется на два компонента: варьирование между вариантами (Cv)и внутри выборок (Cz). Следовательно, общая изменчивость признака может быть представлена выражением: Су= Сv+Cz. Изменчивость (варьирование) между выборками (вариантами) представляет ту часть общей дисперсии, которая обусловлена действием изучаемых факторов, а дисперсия внутри выборок характеризует случайное варьирование изучаемого признака, т. е. ошибку эксперимента. Общее число степеней свободы (N-1) также расчленяется на две части – степени свободы для вариантов ( l-1 ) и для случайного варьирования ( N-l: (N-1) = (l-1) + (N-l). Если обрабатывают однофакторные полевые опыты при размещении вариантов методом организованных повторений (систематический и метод рендомизированных повторений), общая изменчивость (Су) разделяется на три части: варьирование повторений (СР),вариантов (CV) и случайное (Cz). Общее число степеней свободы (N-1) также расчленяется на три части – степени свободы для повторений (n-1), степени свободы для вариантов ( l-1 ) и для случайного варьирования (n-1)(l-1). Общая изменчивость и общее число степеней свободы могут быть представлены выражениями:
Су = СР + Cv + Cz; (N-1) = (n-1)+(l-1) +(n-1)(l-1). Суммы квадратов отклонений по данным полевого опыта – статистического комплекса с l -вариантами и n -повторениями – находят в следующей последовательности. В исходной таблице определяют суммы по повторениям (Р), вариантам (V)и общую сумму всех наблюдений (∑Х). Затем вычисляются: 1) общее число наблюдений N = ln; 2) корректирующий фактор (поправка) С= (∑Х)2: N; 3) общая сумма квадратов Су = ∑Х 2-С; 4) сумма квадратов для повторений СР=∑Р2: l - С; 5) сумма квадратов для вариантов CV = ∑V2:n-С; 6) сумма квадратов для ошибки (остаток) CZ = CY -CP -CV. Две последние суммы квадратов (CV) и (Cz)делят на соответствующие им степени свободы, т. е. приводят к сравниваемому виду – одной степени свободы вариации. В результате получают два средних квадрата (дисперсии): вариантов Эти средние квадраты и используют в дисперсионном анализе для оценки значимости действия изучаемых факторов. Оценка проводится путем сравнения дисперсии вариантов (s2v)с дисперсией ошибки (s2z) по критерию Fф= s2v/ s2z. Теоретическое значение критерия (Fт)для принятого в исследовании уровня значимости (приложение Б) определяют с учетом числа степеней свободы для вариантов ( l-1 )- по горизонтали и ошибки ( N-l ) при размещении вариантов в полевом опыте методом полной рендомизации или (n-1)(l-1) при размещении вариантов методом организованных повторений – по вертикали. В большинстве случаев избирают 5 %, а при более строгом подходе 1 % или даже 0,1% уровень значимости. По результатам дисперсионного анализа необходимо сделать предварительный вывод (проверить нулевую гипотезу). Для проверки нулевой гипотезы сравнивают Fф с Fт. Нулевая гипотеза (Н0) – предположение об отсутствии реального различия между фактическим наблюдением и теоретическим предположением. Например, различия между средними значениями вариантов по урожаю, его качеству, высоте растений и т.д. Для двух средних арифметических
Если Fф < Fт, то нулевая гипотеза H0:d = 0 не отвергается (или подтверждается). Это значит, что различия ( d ) по вариантам опыта несущественны и по результатам исследований делают окончательный вывод об одинаковом влиянии вариантов на результативный признак и использование значения – НСР (наименьшая существенная разность) для составления выводов не имеет смысла. Если Fф Для оценки существенности частных различий определяются: ошибка опыта ошибка разности средних наименьшая существенная разность НСР05 = t05Sd .. Теоретическое значение критерия Стьюдента- t (приложение А) для 5 % уровня значимости (t05) при степени свободы ошибки ( N-l ) при размещении вариантов в полевом опыте методом полной рендомизации или (n-1)(l-1) при размещении вариантов методом организованных повторений. Критерий НСР05 = t05Sd указывает предельную ошибку для разности двух выборочных средних. Сравнивая отклонения по опытным вариантам от контроля (стандарта) со значением НСР, делают выводы. Если фактическая разность d<HCP независимо от знака, то она несущественна. Это означает, что сравниваемые варианты оказывают одинаковое влияние на результативный признак. Если d По результатам дисперсионного анализа (приложение В) необходимо сделать предварительный вывод (проверить нулевую гипотезу). Для этого сравнивают критерий Фишера фактический (Fф) с критерием Фишера табличным (Fт). Из представленных результатов дисперсионного анализа (приложение В – по таблице В.1.2) следует, что Fф= 7,88 >Fт= 3,33. Это означает наличие существенности различий между вариантами в данном опыте, нулевая гипотеза (Но: d = 0) отвергается. Однако неизвестно, между какими вариантами имеются существенные различия. Для этого составляют итоговую таблицу (таблица 1). Рассчитывают среднюю величину результативного признака по вариантам (например, урожайность, приложение Г), средняя урожайность 1 варианта (норма высева 5 млн шт./га) – Различия между вариантами сравнивают с НСР05. Если фактическая разность d ≥ НСР, то она существенна, а если d < НСР – несущественна.
Таблица 1 – Урожайность ячменя в зависимости от нормы высева
Вывод: Норма высева 5,5 млн шт./га увеличила урожайность ячменя на 0,42 т/га (контроль 3,31 т/га) при НСР05 0,19 т/га. По норме высева 6,0 млн шт./га отмечено существенное снижение урожайности на 0,26 т/га. По нормам высева 3,5; 4,0 и 4,5 млн шт./га разница урожайности составила в пределах ошибки опыта. Норма высева 5,5 млн шт./га в сравнении со всеми изучаемыми нормами высева обеспечила достоверную прибавку урожайности ячменя.
Задание. Обработать методом дисперсионного анализа данные однофакторного полевого опыта, проведённого методом организованных повторений на компьютере по программе Ехсеl и составить вывод по полученным результатам. Данные для выполнения задания приведены в приложении Г. Порядок работы: 1. Копировать образец (Однофак. орг. повт.), вставить на рабочий стол и переименовать. 2. Открыть Лист1. Вместо названия результативного признака в образце (Товарная урожайность сортов белокочанной капусты, т/га ), копировать из задания название примера 1 и вставить. 3. В таблице исходных данных изменить название вариантов по своему примеру, вставить свои исходные данные таблицы. Автоматически дисперсионный анализ выполнен, и его результаты будут на Листе 2 (страница 1). 4. Открыть Лист 2 (начиная с буквы А). На Листе 2 обозначить страницы, и выбирается команда Вид – Разметка страницы – обычный – ОК. 5. Необходимо сохранить данные Листа 2 (страница 1-это рабочая ссылками) без ссылок на свободной странице. Копировать данные Листа 2 (страница 1) и вставить на свободную страницу (Листа 2) через специальную ставку, активировать ячейку на свободной странице (верхнюю левую) и выбирается команда правой кнопкой мыши – Специальная ставка – Форматы – ОК – Специальная ставка – Значения и форматы чисел – ОК. В результате отменяются все формулы и ссылки, и получается (F05, Fф, НСР05), необходимо их отформатировать поставить подстрочно (F05, Fф, НСР05), и выбирается команда правой кнопкой мыши – Формат ячеек – Шрифт – вкладка подстрочный – ОК или копировать из образца и вставить в свой пример. Для возведения в степень, ( например м2)выполнить команду Формат ячеек – вкладка Выравнивание, установить флажок надстрочный – ОК. 6. На Листе 1 теперь можно в таблицу исходных данных внести результаты другого учета, изменить название таблицы и автоматически дисперсионный анализ проведен, и его результаты будут на Листе 2 (страница 1). Необходимо сохранить данные Листа 2 (страница 1-это рабочая ссылками) без ссылок. Копировать данные Листа 2 (страница 1) и вставить на свободную страницу (Листа 2) через специальную ставку, активировать ячейку на свободной странице (верхнюю левую) и выбирается команда – Специальная ставка – Форматы – ОК – Специальная ставка – Значения и форматы чисел – ОК. В результате отменяются все формулы и ссылки, и получается (F05, Fф, НСР05), необходимо их отформатировать и поставить подстрочно (F05, Fф, НСР05), и выбирается команда правой кнопкой мыши – Формат ячеек – Шрифт – вкладка подстрочный – ОК или копировать из образца и вставить в свой пример.
7. По результатам дисперсионного анализа необходимо сделать предварительный вывод (проверить нулевую гипотезу). Для этого сравнивают критерий Фишера фактический (Fф) с критерием Фишера табличным (Fт). Если по результатам дисперсионного анализа нулевая гипотеза подтверждается, то в таблицу с отклонениями вместо значений НСР05 вставить подтверждение нулевой гипотезы Fф <F05. Если нулевая гипотеза отвергается, то в таблице с отклонениями выделить разными цветами положительные и отрицательные существенные отклонения и дать оценку (вывод) существенности различий по вариантам опыта. 8. Необходимые функции при выполнении задания: 8.1. Объединение ячеек для ввода текста: предварительно нужно ввести в одну ячейкутекст, затем выделить объединяемые ячейки, включая ячейку с введенным текстом и выполнить команду: Формат ячеек – вкладка Выравнивание, установить флажок Объединение ячеек. Чтобы отказаться от объединения ячеек, следует сделать активную зону объединенных ячеек и, вызвав тот же пункт меню, снять флажок Объединение ячеек. 8.2. Перенос по словам: например в заголовках граф таблицы, предварительно нужно ввести в одну ячейкутекст, выделить её и выполнить команду: Формат ячеек – вкладка Выравнивание, установить флажок Перенос по словам. 8.3. Уменьшение или увеличение разрядности чисел: выделить числа и выполнить команду: Формат ячеек – вкладка Число – Числовой – увеличить или уменьшить число десятичных знаков – ОК.
Таким образом, дисперсионный анализ позволяет определить: 1. общую изменчивость результата (например, урожайности, числа зерен с колоса и т.д.), разделить изменчивость на части в зависимости от структуры опыта; 2. в целом наличие существенных различий по вариантам опыта в результате проверки нулевой гипотезы; 3. существенность различий по НСР и выявить, между средними значениями результата каких вариантов имеются значимые разности.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 3965; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.170.115 (0.013 с.) |

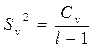 и ошибки
и ошибки  .
. и
и  нулевую гипотезу записывают следующим образом:
нулевую гипотезу записывают следующим образом: 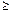 Fт, то нулевая гипотеза отвергается, и это означает, что между средними значениями по вариантам есть существенные различия, полученные разным влиянием вариантов опыта на результативный признак (например, урожайность и т.д.). В этом случае дополнительно оценивают существенность частных различий по НСР и определяют, между какими средними имеются значимые разности.
Fт, то нулевая гипотеза отвергается, и это означает, что между средними значениями по вариантам есть существенные различия, полученные разным влиянием вариантов опыта на результативный признак (например, урожайность и т.д.). В этом случае дополнительно оценивают существенность частных различий по НСР и определяют, между какими средними имеются значимые разности. ;
; ;
; = (3,28+3,35+3,29)/3=3,31 т/га, затем вычисляют среднюю урожайность 2 варианта
= (3,28+3,35+3,29)/3=3,31 т/га, затем вычисляют среднюю урожайность 2 варианта  и т.д. Вычисляют отклонения (разность d) по опытным вариантам в сравнении с контролем т.е. из результата опытного варианта вычитается результат контрольного варианта (
и т.д. Вычисляют отклонения (разность d) по опытным вариантам в сравнении с контролем т.е. из результата опытного варианта вычитается результат контрольного варианта (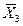 -
- 


