Команды SPSS на выполнение однофакторного дисперсионного анализа

При выборе меню «Analyze > Compare Means > One-Way-ANOVA» (см. рис. 3.2) открывается диалоговое окно «Однофакторный дисперсионный анализ» (рис. 3.12).

В левом поле ок на указываются метки всех переменных, занесенных в базу данных. Из списка всех переменных выбирается категориальный фактор, т.е. переменная, разбивающая данные на группы (категории) (в рассматриваемом примере — «Вид транспорта»), и переносится в поле «Factor».

Далее из списка переменных выбирается другая исследуемая переменная — «зависимая переменная» (в рассматриваемом примере — «Удаленность места отдыха») — и переносится в поле «Dependent List».

Прежде чем нажать кнопку «ОК» и запустить процесс выполнения анализа, следует задать дополнительные команды во вспомогательном диалоговом окне «Опции», которое открывается путем нажатия одноименной кнопки в главном диалоговом окне «Однофакторный дисперсионный анализ» (рис. 3.12 и 3.13).

 

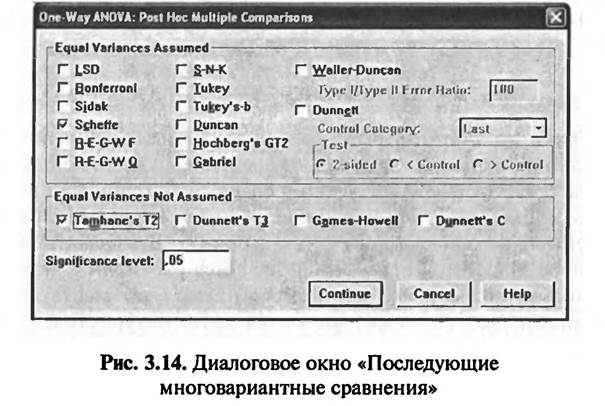
В диалоговом окне «Опции» путем отметки напротив команды «Descr ptive» (см. рис. 3.13) можно задать вывод на экран статистических показателей, описывающих распределение переменной «Удаленность места отдыха» в разных группах респондентов, сформированных в зависимости от используемого ими вида транспорта. Результат выполнения этой команды будет представлен далее в табл. 3.3.

В ходе выполнения однофакторного дисперсионного анализа следует проверить равенство дисперсий распределения зависимой переменной в сравниваемых группах. Равенство дисперсий проверяется при помощи теста Ливина. Для задания на выполнение данного теста в диалоговом окне «Опции» следует сделать отметку напротив команды «Homogenei у of variance test» (см. рис. 3.13). Результаты проведения теста Ливина будут представлены далее в табл. 3.4.

Также в рассматриваемом примере в диалоговом окне «Опции» поставлена отметка напротив команды «Means Plot». В результате выполнения этой команды на экран компьютера выводится график средних значений зависимой переменной в разных группах (категориях). Этот график будет представлен ниже в рассматриваемом примере среди результатов анализа (рис. 3.15).

При нажатии кнопки «Continue» в диалоговом окне «Опции» осуществляется возврат в главное диалоговое окно «Однофакторный дисперсионный анализ» (см. рис. 3.12).

В результате проведения однофакторного дисперсионного анализа согласно описанному выше заданию, т.е. перечню команд, решаются две задачи:

Проверяются равенства дисперсий значений зависимой переменной в сравниваемых группах (категориях).

Выявляются взаимосвязи между исследуемыми переменными, т.е. приводится доказательство неравенства средних значений зависимой переменной в сравниваемых группах (категориях). Решение этих задач не является окончательным результатом

однофакторного дисперсионного анализа. Если взаимосвязь между исследуемыми переменными существует, то следует выяснить, какие именно категории обусловливают существование этой связи. Иными словами, если выясняется, что средние значения зависимой переменной в сравниваемых группах (категориях) не равны, то необходимо выяснить — в каких именно. Для решения этой задачи проводятся дополнительные исследования (Post Нос).

Для выяснения того, в каких же именно группах (категориях) средние значения зависимой переменной в наибольшей степени отличаются друг от друга, проводится многовариантное сравнение этих значений (Multiple Comparison). Данный процесс осуществляется путем проведения так называемых апостериорных тестов.

Команда на проведение апостериорного теста задается в дополнительном диалоговом окне «Последующие многовариантные сравнения» (рис. 3.14), которое открывается путем нажатия кнопки «Post Нос» в главном диалоговом окне «Однофакторный дисперсионный анализ».

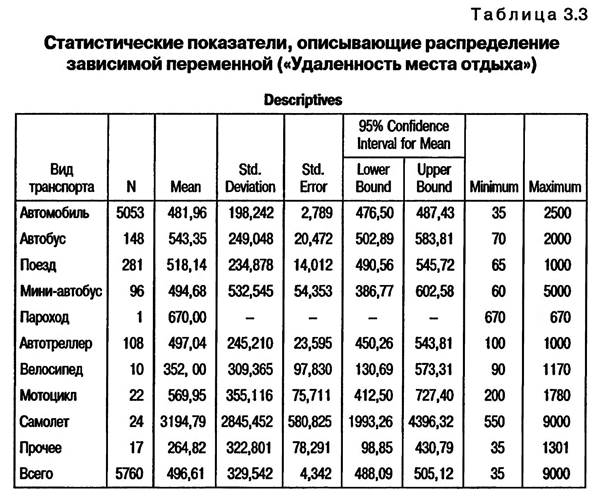
В диалоговом окне «Последующие многовариантные сравнения» представлены различные апостериорные тесты, позволяющие выявить группы, ответственные за результаты дисперсионного анализа.

Правильный выбор апостериорного теста возможен только после проведения теста Ливина на равенство дисперсий. Некоторые тесты могут применяться только в том случае, если дисперсии зависимой переменной в сравниваемых группах (категориях) равны (Equal Variances Assumed). Другие тесты, наоборот, применяются в том случае, если дисперсии значений зависимой переменной в разных группах (категориях) не равны (Equal Variances Not Assumed).

В целях сокоащения количества итераций рекомендуется задать команды на проведение сразу двух тестов: на случай равенства и неравенства дисперсий зависимой переменной в сравниваемых группах. При интерпретации результатов анализа будет выбран нужный вариант.

В рассматриваемом примере в диалоговом окне «Последующие многовариантные сравнения» заданы команды на проведение теста «Scheffe» и «Tamhane», которые наиболее часто используются на практике. После нажатия кнопки «Continue» в этом же диалоговом окне осуществляется возврат в главное диалоговое окно «Однофакторный дисперсионный анализ».

Путем нажатия кнопки «ОК» в главном диалоговом окне запускается процедура выполнения однофакторного дисперсионного анализа.

3.2.3. ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ ОДНОФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА

Среди результатов выполнения задания (перечня команд), описанного выше, в первую очередь на экран компьютера выводится таблица «Descriptives». Она содержит различные статистические показатели, описывающие распределение зависимой переменной в разных группах (категориях). В рассматриваемом примере зависимой переменной является расстояние, преодолеваемое туристами от места проживания до места отдыха. Группами (категориями) являются группы туристов, пользующихся различными видами транспорта для проезда до места отдыха (табл. 3.3).

Статистические показатели, отображенные в таблице «Descriptives»:

• число наблюдений (респондентов) в одной группе (N);

• среднее значение (Mean);

• стандартное отклонение (Std. Deviation);

• стандартная ошибка (Std. Error);

• доверительный интервал (Confidence Interval);

• минимальное и максимальное значения, т.е. самое короткое и самое длинное рассгояние, преодолеваемое туристами с помощью определенного вида транспорта (Minimum, Maximum). Таблица «Descriptives» дает лишь общее представление о распределении значений зависимой переменной в разных группах (категориях). Основная задача данного этапа исследований — проверка практической значимости сформированных групп (категорий).

Как видно из данных табл. 3.3, из числа всех респондентов, давших ответы на вопросы анкеты № 12 и № 14 (5760 человек), только один воспользовался пароходом, чтобы добраться до места отдыха. Данная группа («туристы, выбирающие пароход») должна быть исключена из исследований, поскольку она состоит только из одного респондента и является практически незначимой.

Следующим шагом представления результатов однофактор- ного дисперсионного анализа является представление результатов проверки равенства дисперсий в сравниваемых группах (категориях), т е. результатов теста Ливина (табл. 3.4).

 

Тест Ливина позволяет проверить верность гипотезы: «Дисперсии в рассматриваемых группах равны». Значение расчетного показателя «Significance» в данном случае равно 0,000. Это означает, что исходная гипотеза может быть отклонена с вероятностью ошибки 0%, т.е. гипотеза неверна. Это доказывает, чго дисперсии зависимой величины «Удаленность места отдыха» в сравниваемых группах (категориях) туристов, воспользовавшихся разными ьидами транспорта, не равны.

После результатов проверки равенства дисперсий в сравниваемых группах на экран выводятся результаты однофакторного дисперсионного анализа (ANOVA: Analysis of Variance) (табл. 3.5).

Таблица 3.5 Результаты однофакторного дисперсионного анализа ANOVA   Sum of Squares df Mean Square F Sig. Between Groups 177533022,851   19725891,43 253,245 ,000 Within Groups 447881263,272   77892,394     Total 625414286,122

 

Как отмечалось ранее, однофакторный дисперсионный анализ позволяет проверить вероятность исходной (нулевой) гипотезы о равенстве средних величин более чем в двух группах. В рассматриваемом примере нулевая гипотеза представляет собой утверждение: «Туристы, пользующиеся различными видами транспорта, в среднем преодолевают равные расстояния от места проживания до места отдыха».

Равенство средних значений зависимой переменной в разных группах (категориях) свидетельствует об отсутствии взаимосвязи между исследуемыми переменными. В рассматриваемом примере исходная (нулевая) гипотеза может также быть представлена в виде утверждения: «Не существует взаимосвязи между удаленностью места отдыха и выбором вида транспорта».

Верность исходной (нулевой) гипотезы проверяется при по- мо] ци расчетной величины «Significance», которая в рассматриваемом примере составляет 0,000. Это означает, что исходная гипотеза может быгь отклонена с вероятностью ошибки 0%, т.е. она неверна.

Из результатов анализа данных, представленных в табл. 3.5, можно сделать вывод, что средняя дальность проезда до места отдыха является различной в отдельных группах туристов, выделенных по виду используемого транспорта. Это доказывает существование взаимосвязи между исследуемыми переменными, т.е. удаленность места отдыха влияет на выбор вида транспорта.

Представленные выше выводы не являются окончательным результатом однофакторного дисперсионного анализа. Для получения более точных результатов исследования необходимо выяснить, в каких именно группах отличия средней длительности проезда наиболее значительны. Это возможно путем проведения дополнительных исследований, а именно апостериорного теста.

В рассматриваемом примере была задана команда на проведение тестов «Scheffe» и «Tamhane» (см. рис. 3.14). Поскольку я результате проведения теста Ливина было выявлено неравенство дисперсий, в рассматриваемом примере значимыми являются только результаты теста «Tamhane».

Апостериорные тесты могут проводиться только в том случае, если сравниваемые группы (категории) включают в себя как минимум два наблюдения. В рассматриваемом примере только один из опрошенных туристов воспользовался пароходом для того, чтобы добраться до места отдыха. Для проведения апостериорного теста сначала необходимо исключить данную группу (категорию) из исследований.

Для исключения из исследований группы туристов, воспользовавшихся пароходом, во вкладке редактора данных «Свойства переменных» (Variable View) в столбце «Мissing» следует указать числовой код значения метки «Пароход» — «5» (см. рис. 3.10), после чего следует пересчитать результаты анализа, повторив все операции по заданию команд на выполнение анализа, описанные в предыдущем разделе.

Среди результатов повторного анализа на экране появятся результаты теста «Tamhane» (табл. 3.6). Здесь представлены результаты попарного сравнения средней дальности проезда до места отдыха для разных групп туристов, сформированных по виду используемого транспорта. Сначала сравнивается средняя дальность проезда до места отдыха на автомобиле со средней дальностью проезда другими видами транспорта, затем средняя дальность проезда до места отдыха на автобусе и т.д. Пары, характеризующиеся значительным различием средних величин, обозначаются звездочкой (*).

Как видно из результатов теста «Tamhane», среднее расстояние до места отдыха, преодолеваемое на самолете, существенно отличается от среднего расстояния проезда до места отдыха другими видами транспорта.

Таблица 3.6 Фрагмент таблицы с результатами теста «ГатЛапе» Multiple Comparsions

					95% Confidence Interval
(1) Вцд	(J) Вид транспорта	Mean			Lower	Upper
транспорта		Diffennce (l-J)	Std. Error	Sig.	Bound	Bound
Автомобиль	Автобус	-61,387	20,661	,117	-128,52	5,74
	Поезд	-36.174	14,286	,349	-82,17	9,82
	Мини-автобус	-12,712	54,424	1,000	-191,53	166,11
	Автотреллер	-15,072	23,760	1,000	-92,83	62,69
	Велосипед	129,965	97,870	1,000	-313,22	573,15
	Мотоцикл	-87,990	75,762	1,000	-365,98	190,00
	Самолет	-2712,827*	580,832	,004	-4817,75	-607,91
	Прочее	217,141	78,340	,389	-84,09	518,38
Автобус	Автомобиль	61,387	20,661	,117	-5,74	128,52
	Поезд	25,213	24,808	1,000	-54,70	105,13
	Мини-автобус	48,674	58,080	1,000	-140,91	238,26
	Автотреллер	46,314	31,238	,996	-54,54	147,17
	Велосипед	191,351	99,949	,959	-247,33	630,03
	Мотоцикл	-26,603	78,430	1,000	-309,01	255,80
	Самолет	-2651,440*	581,186	,005	-4756,96	-545,92
	Прочее	278,528	80,923	,098	-25,25	582,31
Поезд	Автомобиль	36,174	14,286	,349	-9,82	82,17
	Автобус	-25,213	24,808	1,000	-105,13	54,70
	Мини-автобус	23,462	56,130	1,000	-160,33	207,25
	Автотреллер	21,102	27,442	1,000	-67,76	109,96
	Велосипед	166,139	98,828	,992	-274,77	607,05
	Мотоцикл	-51,816	76,997	1,000	-331,75	228,12
	Самолет	-2676,653*	580,994	,004	-4781,85	-571,46
	Прочее	253,315	79,535	,177	-48,96	555,59
Мини-автобус	Автомобиль	12,712	54,424	1,000	-166,11	191,53

Аналогичные выводы можно сделать, руководствуясь графическим изображением зависимости средней дальности проезда до места отдыха и видом используемого транспорта (рис. 3.15). Построение данного графика было задано с помощью отметки напротив команды «График средних величин» (Means plot) в диалоговом окне «Опции» (см. рис. 3.13).

Графическое представление зависимости выбора вида транспорта от средней дальности проезда показывает, что для преодоления больших расстояний (в среднем 3000 км) туристы выбирают самолет. Средние расстояния, преодолеваемые с помощью других видов транспорта (поезд, автобус, автомобиль и др.), не намного отличаются друг от друга (примерно 500—700 км).

В итоге можно сделать вывод, что удаленность места отдыха от места жительства туриста в целом влияет на выбор вида транспорта. Если турист должен преодолеть длинный путь (более 1000 км), то он, скорее всего, выберет самолет. Если же расстояние до места отдыха менее 1000 км, то турист воспользуется другим транспортом, при этом дальность переезда не определяет выбор вида транспорта.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие методы статистического анализа основываются на сравнении средних величин?

Как звучит исходная (нулевая) гипотеза, проверяемая в ходе сравнения средних величин, и при помощи какого показателя определяется ее верность?

Каковы цели проведения и возможности применения результатов Г-тестов и дисперсионного анализа?

Какие требования предъявляются к переменным, участвующим в проведении Г-тестов и дисперсионного анализа, относительно типов шкал измерения переменных?

Назовите основные виды Г-тестов и дисперсионного анализа и укажите, в чем состоит различие между ними.

Для чего проводится тест Ливина и как его результаты используются при интерпретации результатов Г-теста?

Для чего и каким образом производится проверка практической значимости исходных данных однофакторного дисперсионного анализа?

Каким образом производится исключение из исследований, проводимых в SPSS, исходных данных для однофакторного дисперсионного анализа, которые оказались практически незначимыми?

Как влияют результаты теста Ливина на ход проведения однофакторного дисперсионного анализа?

Для чего при проведении однофакторного дисперсионного анализа производятся апостериорные тесты (Post Hoc Multiple Compai sons)?

С какой целью и при помощи какой команды SPSS строится график средних величин при проведении однофакторного дисперсионного анализа?