Определение оптимального числа компонентов факторной модели

Как уже было отмечено выше, число групп (компонентов) факторной модели определяется при помощи расчета «характеристических чисел» (Eigenvalues). Эти показатели характеризуют полноту отображения исходной информации в построенной факторной модели.

Значения этих показателей содержатся в таблице «Total Variance Explained», которая выводится на экран компьютера среди прочих результатов факторного анализа (табл. 5.4).

 

Таблица 5.4 Определение числа компонентов факторной модели Total Variance Explained

Component	Initial Eigenvalues	Rotation Sums of Squared Loadings
Total	%ofVai ance	Cumulative %	ТоУ	%ofVai ance	Cumulative %
	2,345	19,544	19,544	1,885	15,710	15,710
	1,600	13,336	32,881	1,859	15,496	31,205
	1,304	10,865	43,745	1,413	11,778	42,983
	1,103	9,191	52,936	1,194	9,953	52,936
	,929	7,740	60,677
	,882	7,351	68,028
	,741	6,178	74,206
	,716	5,967	80,173
	,676	5,632	85,805
	,623	5,191	90,996
	,565	4,704	95,700
	,516	4,300	100,000

Etfrac on Method: Principal Component Analysis.

 

В первом столбце табл. 5.4 (Component) указывается число компонентов различных вариантов факторной модели. В четвертом столбце этой таблицы (Cumulative, %) показан процент информации, сохраненной в процессе группировки исходного массива переменных с помощью факторной модели. Например, если число факторов в факторной модели равно числу переменных исходного массива (в нашем примере 12), т.е. группировка переменных не производится, исходная информация будет сохранена на 100%.

Во втором столбце таблицы (Total) указываются значения «характеристических чисел» (Eigenvalues). В рассматриваемом примере было задано условие: значение «характеристических чисел» должно быть больше единицы (Eigenvalues over 1) (см. рис. 5.7). Максимальное значение компонентов фа^орной модели, в которой данный показатель превышает единицу, составляет 4. Это означает, что оптимальное число групп (факторов) в факторной модели составляет 4.

Как видно из данных, представленных в табл. 5.4, факторная модель, состоящая из 4-х факторов, сохраняет лишь 52,936% исходной информации. Как отмечалось ранее, при группировке исходного массива переменных потеря информации неизбежна. При построении факторной модели следует стремиться к минимизации потерь информации.

Сохранение информации всего лишь на 52,936% является не очень хорошим показателем. Однако, принимая во внимание, что в ходе факторного анализа число переменных сократится в 3 раза (с 12 до 4), а потеря информации составит менее 48%, применение построенной факторной модели следует считать целесообразным.

В ходе формирования задания на проведение факторного анализа также было запрошено построение графика «Screen plot» (см. рис. 5.7), с помощью которого можно также определить оптимальное число групп. Результаты выполнения этой команды представлены на рис. 5.10.

 

На рис. 5.10 представлен график, отображающий зависимость между «характеристическими числами» (Eigenvalues) и числом компонентов факторной модели (Component Number). При изменении количества факторов с 5 до 12 данный график представляет собой практически линейную функцию, а при уменьшении числа факторов с 5 до 4 происходит «перелом» графика. Это означает, что оптимальное число компонентов факторной модели (факторов) равно 4.

Таким образом, результаты графического метода определения числа фактор >в подтвердили результаты расчетного метода (см. табл. 5.4). В результате применения обоих методов оптимальное число компонентов факторной модели составило 4.

5.6. ПОСТРОЕНИЕ ФАКТОРНОЙ МОДЕЛИ И ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ

Ротированная матрица компонентов факторной модели

Следующим шагом в представлении результатов факторного анализа является ротированная матрица компонентов (табл. 5.5).

Таблица 5.5

Rotated Component Matrix⁰

	Component
Спокойный отдых	-,041	,095	,809	-,191
Спорт и физические нагрузки	,078	-,047	,002	,886
Удовольствия и развлечения	,762	,058	,013	-,064
Знакомства и общение	,683	,193	,197	-,102
Красота и здоровье	,083	-,011	,676	,365
История и традиции	,006	,684	-,006	,098
Общение с природой	-,165	,481	,322	,383
Культурная программа	,143	,649	-,295	-,039
Игры, фестивали и пр.	,423	,310	-,066	,105
Путешествия в соседние страны	,161	,467	,143	-,178
Товары народного промысла	,130	,609	,178	-,037
Ночной/вечерний досуг	,742	-,047	-,129	,150

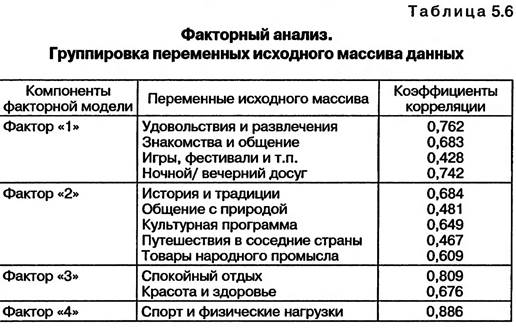
Метод извлечения: анализ главных компонентов. Метод ротации:«Varimax»с нормализацией Кайзера. ^а Ротация получена за 5 итераций.

В табл. 5.5 представлены коэффициенты корреляции, характеризующие связи между переменными исходного массива данных и компонентами построенной факторной модели (факторами). Согласно общему правилу проведения факторного анализа в одну группу (под одним фактором) собираются переменные исходного массива, имеющие наиболее тесную связь (самое большое значение коэффициента корреляции) с данным компонентом факторной модели.

В табл. 5.5 отмечены максимальные значения коэффициентов корреляции, свидетельствующие о наиболее тесной взаимосвязи переменных исходного массива с компонентами факторной модели. На основе этих данных производится группировка переменных исходного массива, представленная в табл. 5.6.

Следующим шагом факторного анализа является ингерпрета- ция результатов, т.е. определение названия каждого фактора (компонента факторной модели). Название фактора подбирается специалистами, проводящими исследование, исходя из логики и названий переменных, объединенных эт им фактором.

В нашем примере были подобраны следующие названия компонентов факторной модели:

• Фактор «/» — «Развлечения».

• Фактор «2» — «Специальные предложения Восточной Баварии».

• Фактор «3» — «Спокойный отдых».

• Фактор «4»— «Спорт».

Первый фактор получил название «Развлечения», поскольку он объединяет переменные исходного массива, так или иначе связанные с развлечениями и увеселительными мероприятиями.

Переменные, объединенные фактором «2», связаны с культурной программой отдыха. Лишь одна переменная — «общение с природой» — кажется случайно попавшей в эту группу. Однако ее можно интерпретировать таким образом, что для туристов, ценящих общение с природой, важны такие мотивы выбора места отдыха, как уникальный ландшафт, лесные массивы и водоемы Восточной Баварии. При такой интерпретации переменная «общение с природой» близка по смыслу переменным, связанным с уникальной культурной программой отдыха в Восточной Баварии. Таким образом, фактор «2» получил название «Специатьные предложения Восточной Баварии».

Фактор «3», объединяющий переменные «спокойный отдых» и «красота и здоровье», получил название «Спокойный отдых». Переменная «спорт и физические нагрузки» оказалась единственной переменной в группе «4» — «Спорт».

Как отмечалось ранее, при построении факторной модели неизбежна частичная потеря информации. Потеря информации особо ощутима в случае, если отдельные переменные исходного массива данных имеют высокие значения коэффициентов корреляции сразу с несколькими факторами.

Например, переменная «красота и здоровье» имеет достаточно высокий коэффициент корреляции с фактором «Спорт» (0,676) и фактором «Спокойный отдых» (0,365) (см. табл. 5.5). Это говорит о том, что туристы, занимающиеся спортом, достаточно большое внимание уделяют заботе о красоте и здоровье, но все же в меньшей степени, чем туристы, предпочитающие спокойный отдых. Построенная функциональная модель ведет к частичной потере информации, поскольку предполагает, что забота о красоте и здоровье важна только для туристов, предпочитающих спокойный отдых, и не важна для других туристов.

Переменная «общение с природой» также имеет высокие коэффициенты корреляции с факторами «Специальные предложения Восточной Баварии» (0,481), «Спокойный отдых» (0,322) и «Спорт» (0,383) (см. табл. 5.5). Это свидетельствует о том, что общение с природой важно как для туристов, занимающихся спортом, так и для тех, кто предпочитает спокойный отдых. Факторная модель связана с частичной потерей информации, поскольку предполагает, что общение с природой важно только для туристов, интересующихся специальными предложениями Восточной Баварии.

Иллюстрация результатов факторного анализа представлена на рис. 5.11.

Несмотря на то что факторная модель ведет к существенной потере информации исходного массива данных (почти 47%), применение данной модели является весьма целесообразным. Как уже было отмечено выше, при потере информации менее чем наполовину, число переменных исходного массива уменьшается в 3 раза.