Интерпретация результатов простого регрессионного анализа

В качестве результатов линейного регрессионного анализа SPSS выводит на экран компьютера три таблицы: «Model Summary», «ANOVA» и «Coefficients» (табл. 4.1,4.2 и 4.3).

Таблица 4.1 Model Summary¹³

			Adjusted R	Std. Error of
Model	R	R Square	Square	the Estimate	Durbin-Watson
	,605^е	.366	,366	587,685	1,874

^а Predictors - влияющие переменные (константа): расходы на проживание. ^b Dependent Variable - зависимая переменная: общие расходы на отдых.

 

В табл. 4.1 представлены основные показатели, оценивающие качество линейной модели, построенной в результате проведения регрессионного анализа.

В рассматриваемом примере значение коэффициента детерминации R составляет 0,605 (>0,5), что свидетельствует о наличии тесной линейной взаимосвязи между суммой общих расходов на проведения отпуска и суммой, уплачиваемой туристами за проживание в гостинице или пансионе.

Коэффициент R-квадрат (R Square) в рассматриваемом примере составляет всего 0,366. Это означает, что построенная регрессионная модель описывает только 36,6% случаев, когда увеличение суммы оплаты за проживание в гостинице или пансионе влечет за собой увеличение общих расходов на проведение отпуска. Это необходимо учитывать при применении результатов анализа в прогнозировании расходов туристов.

Значение теста Дарбина—Уотсона на автокорреляцию в рассматриваемом примере составляет 1,874 (см. табл. 4.1), т.е. близко к 2. Это говорит об отсутствии систематических связей между остатками, т.е. между отклонениями наблюдаемых (эмпирических) значений от теоретически ожидаемых (расчетных).

Таблица 4.2 ANOVA^b Model Sum of Squares df Mean Square F Sig. 1 Регрессия 190625404,593   193625404,6 560,625 ,000^a Остатки 335012199,316   345373,401     Всего 528637603,910

^а Predictors - влияющие переменные (константа): расходы на проживание. ^b Dependent Variable - зависимая переменная: общие расходы на отдых.

В последнем столбце таблицы «ANOVA» (см. табл. 4.2) значение показателя «Статистическая значимость» (Sig.) должно быть меньше или равно 0,5. В рассматриваемом примере этот показатель составляет ноль. Это свидетельствует о том, что регрессионная модель, построенная на основе данных респондентов, попавших в выборку, справедлива для всей генеральной совокупности в целом.

Результаты регрессионного анализа, описывающие построенную регрессионную модель, представлены в табл. 4.3.

Таблица 4.3

Coefficients8

Model	Unstandardized Coefficients	Standarc zed Coeffic Hits	t	Sig.
B	Std. Error	Beta
1 (Constant)	642,273	31,526		20,373	,000
Расходы на проживание	1,596	,067	,065	23,678	,000

а Dependent Variable - зависимая переменная: общие расходы на отдых.

В столбце «В» таблицы «Коэффициенты» представлены параметры построенной регрессионной модели. В рассматриваемом примере уравнение регрессии имеет вид у = 642,273 + 1,596х.

Величина «Constant» показывает значение зависимой переменной при нулевом значении независимой переменной. Построенная регрессионная модель в рассматриваемом примере показывает, что если турист не тратит никаких денег за проживание в отеле или пансионе (например, если он остановился у друзей или живет в палатке), то его общие расходы на проведение отпуска в среднем составят 642,273 евро.

В следующем столбце табл. 4.3 представлены стандартные ошибки (Std. Error). При доверительном интервале 95% каждый коэффициент может отклоняться от средней величины на ±2 х xStd.Error. Например, сумма общих расходов на проведение отпуска при нулевых затратах на проживание в гостинице или пансионе может отклоняться от среднего значения (642,273 евро) на ± 2 • 31,526, т.е. на ± 63,052 евро.

Значение коэффициента регрессии независимой переменной «Затраты на проживание в гостинице или пансноне» в построенной модели составпяет 1,596. Это означает, что увеличение затрат на проживание в отеле или пансионе на 1 евро влечет за собой увеличение суммы общих затрат на проведение отпуска на 1,596 евро.

4.1.4. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРОСТОЙ РЕГРЕССИОННОЙ МОДЕЛИ В SPSS

Как уже было отмечено выше, основным достоинством линейной регрессии является возможность наглядного представления результатов анализа в виде линейного графика в двухмерной системе координат. Задание на построение такого графика осуществляется в SPSS в опции «Graphs».

При выборе меню «Graphs > Scatter» на экране появляется диалоговое окно «Scatte/Dot» («Диаграмма рассеяния»), в котором следует выбрать тип диаграммы. В данном случае следует выбрать диаграмму «Si rnple Scatter» (рис. 4.7).

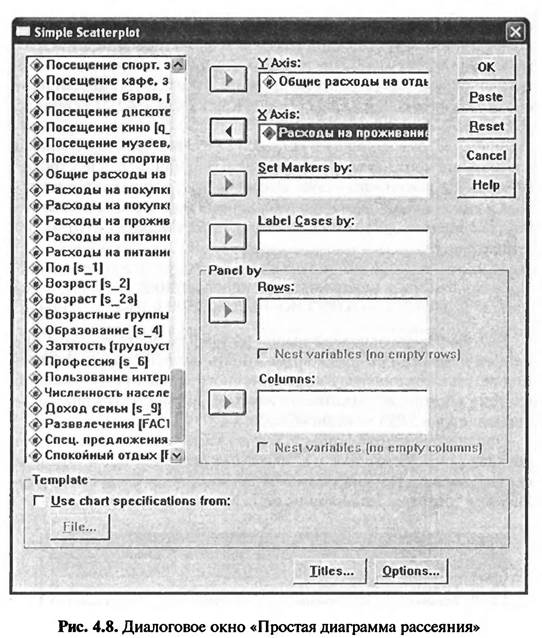
Путем нажатия кнопки «Define» в диалоговом окне «Scatte/Dot» («Диаграмма рассеяния») на экране компьютера появляется новое диалоговое окно «Simple Scatterplot» («Простая диаграмма рассеяния») (рис- 4.8).

В левом поле диалогового окна «Простая диаграмма рассеяния» указываются метки всех переменных, содержащихся в исходном файле данных SPSS. Из списка меток всех переменных следует выбрать метку зависимой переменной и перенести ее в правое поле окна «YAxis». В рассматриваемом примере это метка переменной «q_45_2» — «Общие расходы на отдых».

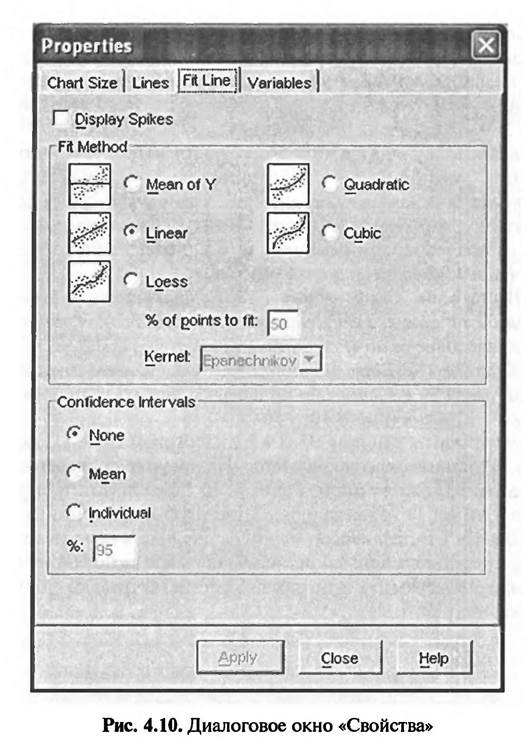
Далее из списка всех переменных, представленных в левом поле окна «Простая диаграмма рассеяния», следует выбрать метку независимой переменной и перенести ее в правое поле окна «XAxis». В рассматриваемом примере это метка переменной «q_47__2» — «Расходы на проживание».

Нажав кнопку «ОК» в диалоговом окне «Простая диаграмма рассеяния», мы закрываем данное окно, и на экране компьютера появляется диаграмма рассеяния. К данному рисунку следует подвести курсор мыши и нажать кнопку мыши два раза. В результате этой операции на экране появится диалоговое окно «Chart Editor» («Редактор диаграмм») (рис. 4.9).

В диалоговом окне «Chart Editor» следует выбрать меню «Elements > Fit Line at Total», в результате чего на экране появится новое диалоговое окно «Properties» («Свойства») (см. рис. 4.9).

Во вкладке «Fit Line» («Приближенная линия») диалогового окна «Properties» («Свойства») следует отметить линейный вид графика — «Linear» (рис. 4.10).

После нажатия кнопки «Close» в диалоговом окне «Свойства» (рис. 4.10) данное окно закрывается. На рисунке построенной ранее диаграммы рассеяния (см. рис. 4. 10 — без линии тренда) появляется линия, отображающая линейную регрессионную модель. Следует отвести курсор мыши от рисунка и нажать клавишу мыши, в результате чего закроется диалоговое окно «Chart Editor» («Редактор диаграмм») и на экране останется только построенный график (рис. 4.11).

На рис. 4.11 представлено графическое изображение регрессионной модели у = 642,273 + 1,596х. Используя эту модель, можно прогнозировать, как будут изменяться общие расходы на отдых при изменении расходов на проживание в гостинице/пансионе для туристов, отдыхающих в курортной зоне «Баварский лес».

 

Построенная нами регрессионная модель описывает только 36,6% всех данных, полученных в результате опроса туристов. Это говорит о том, что вероятность ошибки при использовании данной регрессионной модели в целях прогнозирования достаточно велика.