
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсионный анализ (зависимые и независимые переменные)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рис. 1.1. Взвешенная случайная выборка
В качестве недостатков этого метода формирования статистической выборки следует отметить необходимость знания структуры генеральной совокупности и сложность организации сбора информации на практике. 3. Клюмпенная выборка используется также в том случае, если генеральная совокупность разделена на группы (клюмпены). Из общего числа клюмпенов случайным образом выбирается один, который используется как статистическая выборка. Все элементы клюмпена становятся элементами статистической выборки. Этот метод формирования выборки часто называется «региональным»: генеральная совокупность — страна (город), выборка — республика (район города) (рис. 1.2). Например, если в качестве генеральной совокупности выступают все студенты города Москвы, то для формирования клюмпенной выборки случайным образом может быть выбран один из столичных вузов. Достоинство клюмпенной выборки состоит в более простой организации процесса сбора информации и снижении затрат (экономия на транспортных расходах). Основным недостатком данного метода формирования статистической выборки является клюмпенный эффект, который состоит в том, что клюмпены могут существенно отличаться друг от друга по структуре, что обусловливает низкую степень репрезентативности клюмпенной выборки. Едва ли по данным, собранным при участии студентов только одного московского вуза, можно судить обо всех студентах города Москвы.
При формировании круга респондентов для проведения маркетинговых исследований использование случайной выборки не всегда возможно или целесообразно. Например, при сборе информации посредством наблюдения не всегда возможно заранее четко определить круг людей, которые окажутся в поле зрения наблюдателя. Формирование случайной статистической выборки предполагает возможность сбора информации по каждому элементу генеральной совокупности. Однако такая возможность не всегда существует на практике. Например, проведение исследований на территории вуза требует получения согласия его администрации. Одно это обстоятельство может стать серьезным препятствием быстрому и оперативному сбору информации. На практике часто применяют эмпирическую выборку, когда в круг респондентов для сбора информации включается каждый «первый встречный», согласный принять участие в исследовании (при проведении наблюдения такое согласие не всегда является необходимым условием). В этом случае возможно также использование квотированной выборки, когда структура неэмпирической выборки определена заранее (например, 50% женщин и 50% мужчин). Эмпирическая выборка характеризуется низкой степенью репрезентативности. Результаты исследований при использовании эмпирической выборки зависят от места и времени сбора информации. Например, при изучении досуга студентов города Москвы результаты исследования будуг определяться тем, где происходит сбор информации — у входа в ночной клуб или в библиотеку. Статистическая выборка не используется при проведении качественных маркетинговых исследований, например исследований в форме экспертных опросов или фокус-групп. В этих случаях круг респондентов для проведения маркетинговых исследований формируется при помощи целенаправленной выборки. При осуществлении целенаправленной выборки для участия в исследовании отбираются респонденты, которые могут предоставить наиболее точную и полную информацию (формирование экспертной группы), при участии которых можно организовать наиболее плодотворную дискуссию (формирование фокус- группы). В данном случае из числа потенциально возможных респондентов выбираются те, которые обладают наиболее ценной информацией и готовы поделиться ею для проведения исследований. При формировании статистической выборки следует решить следующие вопросы: 1. Определит ь генеральную совокупность. 2. Определить размер выборки. 3. Выбрать метод формирования выборки. Определение генеральной совокупности позволяет ответить на вопрос: «Из каких потенциальных респондентов следует производить выборку?» Это не всегда является очевидным. Например, кого следует привлекать для сбора информации при изучении вопросов семейного отдыха: жен, мужей, других членов семьи, работников туристических фирм или, может быть, всех вместе? Чтобы ответить на этот вопрос, исследователям необходимо решить, какого типа информация им нужна и кто ею, скорее всего, обладает (Янкевич, Безрукова, 2002. С.111). Размер выборки определяется экономической целесообразностью сбора информации. Увеличение размера выборки способствует повышению репрезентативности и, следовательно, точности результатов исследования, однако это сопряжено с дополнительными затратами. В этом случае необходимо взвешивать экономическую ценность получаемой информации и затраты, связанные с ее сбором. Сбор первичной информации в рамках статистической выборки осуществляется в форме проведения опроса, наблюдения или эксперимента. КЛАСТЕРНЫЙ АНАЛИЗ Кластерный анализ — метод классификации объектов по заданным признакам. Задача кластерного анализа состоит в формировании групп: • однородных внутри (условие внутренней гомогенности); • четко отличных друг от друга (условие внешней гетерогенности). Целью кластерного анализа в маркетинге является определение целевых групп потребителей, для которых было бы целесообразно разработать специальное торговое предложение, т.е. уникальную комбинацию инструментов маркетинга. Пример. Курильщики сигар, возраст и уровень доходов которых известны, исследуются на предмет возможности их разделения на однородные группы (кластеры) (рис. 1.3).
В варианте В однородные кластеры не выявлены. Следовательно, целенаправленная дифференциация торгового предложения невозможна. В варианте А выявлены две однородные группы курильщиков сигар: «старые и бедные», «молодые и богатые», которых можно считать двумя целевыми группами потребителей. В этом случае целесообразно разработать два специальных торговых предложения уникальных по цене, уровню качества продукции, упаковке, системе продвижения товара и т.д. (Schmalen, 2003. S.401). Элементы, включаемые в один и тот же кластер, имеют разную степень схожести (уровень отличия друг от друга). Техника кластерного анализа заключается в выявлении уровня схожести всех исследуемых элементов и последовательном объединении элементов в порядке возрастания уровня различия между ними. Число выявленных кластеров зависит от заданного уровня схожести (различия) элементов, включаемых в один кластер. Техника кластерного анализа может быть проиллюстрирована дендограммоi, составляемой при помощи статистической компьютерной программы, втом числе SPSS (рис. 1.4). На рис. 1.4 изображен результат кластерного анализа 18 предприятий розничной торговли, которые предлагают в качестве «особого предложения» (товары со скидками) один и тот же набор продуктов (примерно 50 наименований): молочные продукты, чистящие средства, косметика и т.д.
Целью кластерного анализа в данном случае является ответ на вопрос: возможно ли разделение исследуемых предприятий розничной торговли на кластеры в зависимости от их ценовой политики в плане формирования «особых предложений» В результате проведения кластерного анализа было выявлено три кластера: А, В и С (рис. 1.4). Предприятия розничной торговли 6, 18, 16, 1,5, 15 (кластер А), так же как и 12, 2, 9, 17, 10 (кластер С), проводят одинаковую ценовую политику при формировании «особых предложений» (это, в частности, магазины торговых сетей EDEKA и REWE). Предприятия розничной торговли, вошедшие в кластер В («Прочие»), не имеют одинаковой ценовой политики, но, тем не менее, их «особые предложения» имеют схожую ценовую структуру. Их можно объединить в одну группу только при задании определенного допустимого уровня их отличия друг от друга (Schmalen, 19. S. 402). При повышении допустимого уровня отличия исследуемых элементов (снижении требований к однородности кластера) возможно объединение кластеров В и С, а затем присоединения к ним кластера А. ДИСКРИМИНАНТНЫИ АНАЛИЗ Дискриминантный анализ проводится с целью выявления различий между исследуемыми группами. Например, могут быть исследованы группы потребителей конкурирующих товаров (или покупатели конкурирующих брендов) на предмет того, существуют ли различия между исследуемыми группами по заданным признакам. Иными словами, цель анализа — выяснить, можно ли составить «типичный портрет покупателя» для каждой исследуемой группы по заданным характеристикам. Пример. Владельцев BMW и VW возраст и доходы которых известны, исследуют на предмет того, можно ли разделить их (дискриминация) на две группы — «типичных владельцев BMW» и «типичных владельцев VW», так, чтобы группы владельцев характеризовались определенным уровнем дохода и возрастом (рис. 1.5).
На рис. 1.5 в системе координат заданных характеристик отмечены сочетания возраста и дохода каждого исследуемого владельца автомобилей (BMW и VW). В ходе дискриминантного анализа предпринимается попытка разделить существующие группы автовладельцев по возрасту и уровню дохода при помощи дискриминантной линий. Дискрими- нантная линия должна быть проведена таким образом, чтоб комбинации характеристик владельцев автомобилей разных марок оказались расположенными по разные стороны линии и возможных пересечений было бы как можно меньше. В этом случае можно составить портрет «типичного владельца автомобиля определенной марки» по заданным характеристикам. В варианте В возможны различные положения дискриминантной линии, при которых число пересечений будет в равной степени многочисленным. В данном случае невозможно разделить владельцев BMW и VW по уровню дохода и возрасту, т.е. не существует «портрета типичного владельца» BMW или VW. В варианте А большая часть комбинаций уровней дохода и возраста владельцев VW лежит слева от дискриминантной линии, а владельцев BMW — справа. Это говорит о том, что владельцы BMW характеризуются более высоким уровнем дохода и относительно молоды по сравнению с владельцами VW (Schmalen, 2002. S. 403). Характеристики «типичного потребителя», выявленные в результате проведения дискриминантного анализа, используются при прогнозировании поведения покупателей. Руководствуясь выявленными характеристиками «типичного покупателя», можно спрогнозировать, в пользу какого именно товара будет принято решение о покупке. В нашем примере (см. рис. 1.5) молодого человека с высоким уровнем дохода, желающего приобрести автомобиль, можно рассматривать как потенциального владельца BMW. Если кластерный анализ выявляет возможность разбиения совокупности респондентов на группы, то дискриминантный анализ выявляет возможность установления различий уже существующих групп респондентов. В настоящее время на практике для прогнозирования поведения потребителей используется более совершенный статистический метод — логистической регрессии. Этот метод позволяет не только ответить на вопрос, какой именно товар потребитель выберет скорее всего, но и определить вероятность, с которой потребитель выберет тот или иной товар. висимая переменная Y). В варианте В существует много возможностей проведения регрессионной линии, когда сумма квадратов расстояний от точек эмпирических значений до регрессионной линии будет примерно одинаковой. Возникает так называемый эффект пропеллера. В этом случае линейная зависимость между исследуемыми переменными отсутствует. В варианте А можно найти наилучший вариант положения регрессионной линии при помощи метода наименьших квадратов. В этом случае действительно существует прямая линейная зависимость между уровнем доходов населения и объемом розничной торговли (Schmalen, 2002. S. 405). Результаты регрессионного анализа используются для составления прогнозов изменения количественных переменных путем перенесения выявленных тенденций на будущие периоды. В рассматриваемом примере (см. рис. 1.6 — вариант Л) между уровнем дохода населения (X) и объемом торгового оборота (У) существует линейная зависимость У = с + b - X. Если существует достаточно надежный прогноз относительно роста доходов населения (X), тогда исходя из данных прогноза (Л") и регрессионной зависимости (У = а + b • X) можно составить прогноз роста объемов оборота розничной торговли (У). Использование регрессионного анализа в прогнозировании сопряжено с рядом проблем. Во-первых, исходя из наличия достаточно устойчивой статистической зависимости не всегда можно делать выводы о существовании каузальной (причинно-следственной) взаимосвязи. В нашем примере результаты регрессионного анализа не доказывают того, что растущий уровень доходов населения является причиной роста объемов оборота розничной торговли. Во-вторых, результаты регрессионного анализа могут быть использованы для построения прогнозов только в случае верности «гипотезы стабильности во времени», т.е. если не происходит никаких структурных изменений. Гипотеза стабильности во времени предполагает изменение во времени только исследуемых переменных, все прочие величины являются постоянными. В приведенном выше примере рассматривается влияние уровня дохода на оборот розничной торговли. Предполагается, что степень влияния прочих факторов (например, цены, склонности потребителей к накоплению и т.д.) остается неизменной. На практике результаты регрессионного анализа используются для составления прогнозов, как правило, в сочетании с опросами Регрессионный анализ — метод выявления статистической зависимости между исследуемыми переменными. На основе анализа эмпирических данных (данных, собранных в ходе проведения исследования) описывается не только сам факт существования статистической зависимости, но также описывается и математическая формула функции зависимости исследуемых переменных. Современная техника регрессионного анализа позволяет описывать функции зависимости исследуемых переменных различных видов. Самая простая — линейная функция, определяемая при помощи линейного регрессионного анализа. Стандартная модель простой линейной регрессии имеет вид Y=a+b*X где X — независимая переменная (фактор, влияющий на объект исследования); Y — зависимая переменная (объект исследования); a, b — постоянные величины (параметры модели).
Определение параметров модели (а, b) осуществляется путем применения метода наименьших квадратов. Регрессионная линия должна быть проведена в «облаке эмпирических значений» таким образом, чтобы сумма квадратов вертикальных и горизонтальных расстояний от каждой точки до регрессионной линии была бы минимальной (рис. 1.6). На рис. 1.6 показана технология выявления зависимости между исследуемыми переменными: уровнем дохода населения (независимая переменная X) и объемом оборота розничной торговли (за экспертов. Такая комбинация количественных и качественных методов маркетинговых исследований соединяет точность математических расчетов со знаниями и интуицией экспертов. ФАКТОРНЫЙ АНАЛИЗ Факторный анализ — метод, который позволяет сгруппировать большое число переменных (факторов, влияющих на предмет исследования) и свести их к минимальному числу «обобщающих факторов». Группировка данных производится по принципу: · переменные, имеющие между собой высокую степень корреляции (тесную взаимосвязь), объединяются в один фактор; · переменные, отнесенные к разным «обобщающим факторам», имеют между собой низкую степень корреляции (слабую взаимосвязь). Факторный анализ производится в том случае, если существует огромный массив данных, который необходимо уменьшить («сжать») для проведения дальнейших исследований. Например, существует база данных по результатам опроса, в ходе которого туристы, отдыхающие в курортной зоне «Баварский лес», оценивали эту курортную зону. Респонденты оценивали степень важности для них каждого из 13 предложенных мотивов выбора места отдыха (табл. 1.2). Предположим, исследователям необходимо провести кластерный анализ туристов, отдыхающих в курортной зоне «Баварский лес», по таким характеристикам, как гражданство, уровень дохода и мотив выбора места отдыха. Проведение кластерного анализа затруднительно из-за больших размеров массива данных, содержащего информацию о мотивах проведения отпуска в «Баварском лесу», и из-за ограничений мощности вычислительной техники. Для удобства проведения кластерного анализа необходимо уменьшить объем («сжатие») данных при помощи факторного анализа. Таблица 1,2 Результаты факторного анализа, проводимого при оценке курортной зоны «Баварский лес» (адаптировано по: Schmalen, 2002. S. 404)
В ходе факторного анализа осуществляется попарное сравнение исследуемых переменных с целью определения их схожести друг с другом, а также определяется число «группирующих факторов». В табл. 1.2 представлены результаты факторного анализа в рассматриваемом примере. Заданные 13 мотивов выбора места отдыха объединены в 4 фактора, определяющих выбор туристов в пользу «Баварского леса»: 1) гостеприимство по приемлемым ценам; 2) общение с природой; 3) специальное предложение Восточной Баварии; 4) культурная программа. Также в табл. 1.2 представлены коэффициенты корреляции, которые характеризуют степень взаимосвязи между группируемыми переменными и группирующими факторами. Значения коэффициентов корреляции изменяется от-1 до +1. Значение коэффициента корреляции, близкое к нулю, указывает на низкую степень взаимосвязи. Например, национальный колорит и самобытность «Баварского леса» (фактор «Специальное предложение Восточной Баварии») не обусловливается приемлемым уровнем цен (коэффициент корреляции 0,00055). Отрицательное значение коэффициента корреляции указывает на существование обратной взаимосвязи. Например, приемлемые цены слабо отрицательно влияют на привлекательность «Баварского леса» с точки зрения общения с природой (коэффициент корреляции 0,01297). Это объясняется тем, что приемлемые цены привлекают множество туристов, что не способствует созданию атмосферы общения с природой. Значение коэффициента корреляции, близкое к -1, указывает на наличие сильной обратной взаимосвязи. Такие случаи в рассматриваемом примере отсутствуют. Если значение коэффициента корреляции близко к +1, это свидетельствует о существовании плотной прямой взаимосвязи. Например, возможность заниматься пешим туризмом в лесу во многом определяет привлекательность рассматриваемого региона для тех, кто ценит общение с природой (коэффициент корреляции 0,81047) (см. табл. 1.2). Характеристики объекта исследования объединяются в один обобщающий фактор при наличии высокой степени корреляции — как позитивной, так и негативной (в рассматриваемом примере встречается только сильная позитивная корреляция). Например, приемлемые цены, вкусная еда, гостеприимство и комфорт отдыха с детьми обобщаются в один фактор привлекательности курорта — «Гостеприимство по приемлемым ценам». При допуске определенной потери информации (в данном случае 30%) впоследствии анализируются не 13 факторов, а только четыре. Такое «сжатие» данных существенно упрощает дальнейшее проведение исследования без существенной потери информации. Факторный анализ целесообразно проводить только в том случае, если он предшествует применению других методов статистического анализа. На практике факторный анализ всегда применяется в комбинации с другими статистическими методами обработки информации. Его можно охарактеризовать как вспомогательный метод, позволяющий упростить исследования путем сокращения анализируемой информации. ДИСПЕРСИОННЫЙ АНАЛИЗ Дисперсионный анализ — метод, при помощи которого исследуется влияние одной или нескольких независимых переменных на одну или несколько зависимых переменных. Например, один и тот же продукт продается в нескольких регионах в упаковке разных типов (табл. 1.3). На основе данных объема продаж, сгруппированных по указанным признакам, нужно определить, имеют ли существенное влияние на результаты продаж: • регион и тип упаковки (основной эффект); • комбинация этих факторов (интерактивный эффект). Виды дисперсионного анализа
ствах массовой информации и др.) на число посетителей в кинотеатре? Пример постановки вопроса двухфакторного дисперсионного анализа (см. табл. 1.3): влияет ли регион и тип упаковки на объем продаж определенного товара? Пример постановки вопроса многомерного дисперсионного анализа: влияют ли регион и тип упаковки на объем продаж и число жалоб потребителей определенного товара? В основе техники проведения дисперсионного анализа лежит сравнение средних величин в разных группах. Например, для того чтобы определить, влияет ли пол студента на успеваемость, необходимо сравнить среднюю успеваемость юношей и девушек. Если средняя успеваемость девушек отличается от средней успеваемости юношей, то можно утверждать, что пол студента влияет на успеваемость, и наоборот. Приведенный пример сравнения средних величин в двух группах (юношей и девушек) осуществляется при помощи Т-теста. Т-тест является частным случаем дисперсионного анализа, в ходе которого осуществляется сравнение средних величин в нескольких группах. Свое название дисперсионный анализ получил благодаря одному из условий сравнения средних величин в разных группах: дисперсии исследуемых величин в разных группах должны быть равны. Дисперсия — показатель, характеризующий рассеяние значений количественного признака вокруг своего среднего значения. Подробно техника сравнения средних величин будет рассмотрена в главе 3 «Сравнение средних величин в SPSS». КОНТРОЛЬНЫЕ ВОПРОСЫ Чем обусловливается необходимость использования статистической выборки при проведении масштабных маркетинговых исследований? В чем заключается основное требование, предъявляемое к статистической выборке? Назовите основные методы формирования статистической выборки, их достоинства и недостатки. Какие виды статистической выборки отличаются наиболее высокой степенью репрезентативности и почему? Назовите основные задачи, решаемые в ходе формирования статистической выборки. Назовите основные методы статистического анализа, применяемые в маркетинговых исследованиях, и их виды. Назовите методы статистического анализа, при помощи которых можно найти ответы на следующие вопросы: а) влияет ли цвет упаковки товара и место его расположения в торговом зале на объем продаж; б) возможно ли разделить постоянных клиентов магазина на группы, используя в качестве критериев разделения объемы совершаемых покупок и частоту посещения магазина; в) насколько увеличится объем продаж товара при увеличении расходов на рекламу на 10% при условии постоянства цены на данный товар; г) по каким социально-демографическим признакам отличаются люди, приобретающие и не приобретающие товар X. 2. ФОРМИРОВАНИЕ ИСХОДНОЙ БАЗЫ ДАННЫХ В SPSS 2.1. СТРУКТУРА РЕДАКТОРА ДАННЫХ Файл исходной базы данных для проведения статистического анализа в SPSS формируется в редакторе данных (Data Editor). Редактор данных имеет две вкладки: «Свойства переменных» (Variable View) и «Значения переменных» (Date View). Данные вкладки представляют собой таблицы, содержащие информацию о данных, собранных для проведения анализа. Во вкладке «Variable View» представлена таблица с данными, описывающими свойства переменных. Каждая строка отображает переменную (вопрос анкеты), каждый столбец — ее свойства (рис. 2.1). В столбце «Name» таблицы «Свойства переменных» указывается имя переменной — как правило, это номер вопроса в анкете. Например, в базе данных, представленной в табл. 2.1, переменная «пол» имеет название «s_l», поскольку в разделе анкеты «социально-демографические признаки» вопрос о поле респондента находился на первом месте. Имена переменных могут содержать буквы латинского алфавита и цифры, а также некоторые символы: $, #. В сумме число знаков не должно превышать «8». Не допускаются пробелы и буквы других алфавитов. Имя переменной должно начинаться с буквы и не может заканчиваться знаком подчеркивания «__». В столбце «Туре» таблицы «Свойства переменных» указывается тип переменной; новые, созданные, переменные по умолчанию являются числовыми (Numeric). Если требуется изменить тип переменной, следует подвести курсор в соответствующую ячейку таблицы, и при нажатии кнопки мыши на экране появится диалоговое окно «Тип переменной» (Van ible Type) (рис. 2.2).
В диалоговом окне «Тип переменной» возможен выбор формата записи значений переменной: Comma (например: 43,675.67); Dot (например: 43.675,67); Scientific notation (например: 43Е+0,4); Dollar (например: $43,675). Аналогичным образом можно выбрать текстовую переменную (Stri ig). Однако применение текстовых переменных в SPSS практически невозможно, поскольку с ними нельзя производить никаких арифметических операций и рассчитывать какие-либо статистические показатели. В поле «Width» диалогового окна «Тип переменной» (см. рис. 2.2) указывается число знаков, используемых для кодировки переменной. Например, для кодировки переменной «пол» используется только один знак («1» — «мужчины» или «2» — «женщины»). Число знаков, используемых для кодировки переменной, можно также указать в столбце «Width» («Формат столбца») таблицы «Свойства переменных» (см. табл. 2.1). В поле «Decimal Places» диалогового окна «Тип переменной» указывается число знаков после запятой при записи значений переменной. Например, для переменной «пол» в поле «Decimal Places» указывается значение 0. Ответы респондентов в данном случае заносятся в базу данных в виде целых чисел («1» — «мужчины» или «2» — «женщины»). Число знаков после запятой при записи значений переменной можно также указать в столбце «Decimals» («Десятичные разряды») таблицы «Свойства переменных». В столбце «Label» таблицы «Свойства переменных» указываются метки переменных. Метка — название, позволяющее описать переменную более подробно, чем имя переменной, она может содержать до 256 символов. В качестве этих символов могут выступагь также буквы русского алфавита. При задании меток переменных часто используются формулировки вопросов, содержащихся в анкете. Например, в качестве метки переменной «пол» в редакторе данных может быть введена фраза: «Укажите, пожалуйста, свой пол». Однако следует помнить, что метка переменной будет отображаться во всех графиках и таблицах, представляющих результаты статистического анализа. Поэтому рекомендуется использовать более лаконичные метки для наглядности представления результатов анализа. В столбце «Values» таблицы «Свойства переменных» (см. рис. 2.1) отображаются значения меток переменных. Если в поле «Label» указывается вопрос анкеты, то в поле «Values» указываются коды возможных вариантов ответа на этот вопрос. Для заполнения поля «Values» необходимо произвести кодировку вариантов отьета. При подведении курсора к соответствующей ячейке таблицы и нажатии клавиши мыши на экране компьютера появляется диалоговое окно «Значение меток переменных» (Value Labels) (рис. 2.3). В диалоговом окне «Значение меток переменных» в поле «Value» указываются числовые коды вариантов ответа, а в поле «Value Label» — их вербальные форму- лировки. При задании вербальных формулировок следует учитывать, что они будут фигурировать впоследствии в графиках и аналитических таблицах. Например, ответ на вопрос о половой принадлежности респондента должен быть не «мужской» («женский»), а «мужчины» («женщины»).
Процедура кодировки производится поэтапно по каждому варианту ответа. В рассматриваемом примере кодировки переменной «пол», сначала в поле «Value» указывается числовой код «1», а в поле «Value Label» — вербальный вариант ответа «мужчины». После нажатия кнопки «Ada» эти данные переносятся в большое поле диалогового окна «Значение меток переменных». Затем подобным образом кодируется вариант ответа «женщины». После нажатия кнопки «ОК» диалоговое окно «Значение меток переменных» закрывается, а указанные в нем данные заносятся в столбец «Values» таблицы «Свойства переменных». В столбце «Missing»(«Пропущенные значения») рис. 2.1 «Свойства переменных» следует указать, какие коды вариантов ответов следует исключить из анализа. В SPSS допускаются два вида пропущенных значений: • Пропущенные значения, определяемые системой (System- defined m»ssirig values). Если в матрице данных есть незаполненные ячейки, система SPSS самостоятельно идент ифицирует их как пропущенные значения. Отсутствие ответа отражается в исходном файле данных в виде запятой. • Пропущенные ответы, задаваемые пользователем (User-defined missing values). Например, среди вариантов ответа на поставленный вопрос можно закодировать отсутствие определенного ответа («98» — «не знаю», «99» — «нет данных») и затем в поле «Ми и ig» указать эти коды, чтобы исключить соответствующие варианты ответа из анализируемых данных. При подведении курсора к соответствующей ячейке столбца «Мissing» и нажатии кнопки мыши открывается диалоговое окно «Пропущенные значения» (рис. 2.4).
По умолчанию в диалоговом окне «Пропущенные значения» отмечается команда «No missing values». Это означает, что пропущенных значений нет, а все варианты ответа на вопрос рассматриваются как допустимые. Если бы нужно было указать коды вариантов ответа, исключаемых из процедуры анализа, то следовало бы выбрать команду «Discrete missing values» и в соответствующих ячейках указать коды «98» и «99» («98» — «не знаю», «99» — «нет данных»). Для одной переменной можно задать до трех пропущенных значений. Существует еще один вариант задания пропущенных значений: «Range plus one optional discrete missing value» («Диапазон плюс единичное пропущенное значение»). Эта команда применялась бы в случае, если бы, например, при заданных значениях переменной «возраст» нужно было бы исключить из исследований респондентов от 20 до 40 лет, а также лиц в возрасте 55 лет. В рассматриваемом примере описания свойств переменной «пол» достаточно сложно представить, чтобы кто-то из респондентов затруднился ответить или не захотел отвечать на вопрос о своей половой принадлежности. Поэтому в поле «Missing» таблицы «Свойства переменных» отсутствуют какие-либо коды вариантов ответа. В столбце «Columns»(«Столбцы») таблицы «Свойства переменных» указывается ширина столбца, содержащего значения соответствующей переменной в таблице другой вкладки редактора данных: «Значения переменных» (Date View) (рис. 2.5). По умолчанию ширина столбца задается «8». В столбце «Alignment» («Выравнивание») таблицы «Свойства переменных» задается положение кодов ответов в таблице «Значения переменных» во вкладке редактора данных «Date View». Они могут быть выровнены по правому краю (Right), по левому краю (Left) или по центру (Center). По умолчанию задается выравнивание по правому краю. Если нужно изменить порядок выравнивания, то следует подвести курсор к соответствующей ячейке столбца «Alignment», и при нажатии клавиши мыши на экране появится меню, содержащее три вышеперечисленных варианта выравнивания данных, из которых следует выбрать желаемый.
В столбце «Measure» («Шкала измерения») таблицы «Свойства переменных» указывается тип шкалы, по которой измеряется переменная. По умолчанию задается метрическая шкала (Scale). В случае необходимости тип шкалы можно изменить. Для этого следует подвести курсор в соответствующую ячейку столбца «Measure» и нажать клавишу мыши, после чего на экране появится меню из трех типов шкалы измерения (рис. 2.6).
В зависимости от вида переменной следует выбрать один из трех типов шкалы измерения: метрическую (Scale), порядковую (Ordinal) или номинальную (Nominal). Поскольку переменная «пол» измеряется по номинальной шкале, то при заполнении таблицы «Свойства переменных» в строке этой переменной в столбце «Measure» выбирается тип шкалы измерения «Nominal». (Более подробно этот вопрос будет рассмотрен в подразделе 2.3 «Типы шкал измерения переменных».) После того как заполнена таблица «Свойства переменных» во вкладке редактора данных «Variable View», следует открыть другую вкладку редактора данных — «Date View». Во вкладке редактора данных «Date View» представлена таблица с данными, описывающими значения переменных. Каждый столбец отображает переменную (вопрос анкеты), каждая строка — отдельное наблюдение (объект сбора информации) (см. рис. 2.5). В качестве объектов сбора информации могут выступать люди, предприятия, продукты, бренды и т.д. На рис. 2.5 представлен фрагмент таблицы, содержащей значения переменных, описанных в таблице «Свойства переменных». Из данных таблицы «Свойства переменных» (см. табл. 2.1) известно, что переменная с именем «s_l» имеет метку «Пол». Метка переменной «пол» имеет два значения: «мужчины» (код «1») и женщины (код «2»). В столбце «s _1» таблицы «Значения переменных» (см. рис. 2.5) содержатся закодированные ответы респондентов на вопрос об их половой принадлежности: «1» или «2». Так, по данным этой таблицы известно, что респондент в строке 1143 — мужчина, а респондент в строке 1144 — женщина. Из данных таблицы «Свойства переменных» также известно, что переменная с именем «s _1а» имеет метку «Возраст». Эта переменная не имеет кодировки (в столбце «Values» отсутствуют значения меток переменных). В столбце «s,1а» таблицы «Значения переменных» содержатся незакодированные ответы респондентов на вопрос об их возрасте. Так, по данным этой таблицы извес
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1644; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.015 с.) |



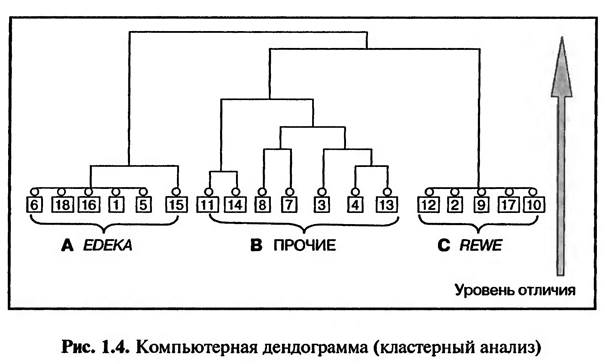
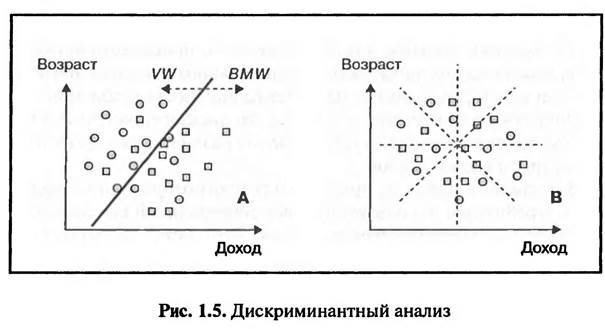


 Рис. 2.1. Редактор данных: вкладка «Свойства переменных» (Variable View)
Рис. 2.1. Редактор данных: вкладка «Свойства переменных» (Variable View)
 Рис. 2.2. Диалоговое окно «Тип переменной»
Рис. 2.2. Диалоговое окно «Тип переменной»


 Рис. 2.5. Редактор данных: вкладка ^Значения переменных» (Data View)
Рис. 2.5. Редактор данных: вкладка ^Значения переменных» (Data View)




