
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однофакторный дисперсионный анализСодержание книги
Поиск на нашем сайте
При проведении экономического анализа часто необходимо оценить влияние на целевую функцию y качественного фактора x. Таким фактором могут быть, например, партии сырья, отрасли промышленности, регионы и т.д. Пусть данные о влиянии некоторого качественного фактора на количественный в форме таблицы. Таблица 1.1. – влияние качественного фактора на исследуемый показатель
Модель зависимости значений
где По выборочным данным можно вычислить: 1) среднее
2) общее среднее
3) общую сумму квадратов отклонений Q0:
4) сумму квадратов, характеризующую влияние фактора x (отклонения между группами)
5) остаточную сумму квадратов, зависящую от ошибки e (отклонения внутри групп)
Тождество дисперсионного анализа имеет вид:
На основании вычисленных сумм квадратов вычисляются: 1) оценка дисперсии относительно общего среднего
где 2) оценка дисперсии «между группами», определяемыми уровнями xj:
где число степеней свободы 3) выборочная оценка дисперсии «внутри групп», вычисляемая как средняя оценка по всем u группам:
с числом степеней свободы Числа степеней свободы должны удовлетворять соотношению
Для того, чтобы сделать вывод о том, влияет ли на исследуемые показатели качественный фактор, сопоставляют дисперсию между группами с общей дисперсией. При этом выдвигают следующие гипотезы: H0: H1:
Оценивание значимости влияния фактора x выполняется по F-критерию Фишера, для чего формируется следующее F-отношение:
Фактор x признается незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости Табличное значение критерия Фишера определяется дл числа степеней свободы u-1 и N-1 и вероятности ошибки Т.е если Если
Результаты дисперсионного анализа сводятся в таблицу 2. Таблица 2 Однофакторный дисперсионный анализ
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.212.29 (0.006 с.) |







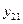





 от фактора столбцов можно представить в следующем виде [1-4]:
от фактора столбцов можно представить в следующем виде [1-4]:
 - общее среднее,
- общее среднее, 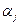 -отклонение от общего среднего для j-го уровня фактора,
-отклонение от общего среднего для j-го уровня фактора, 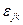 - случайная составляющая.
- случайная составляющая. для каждого уровня фактора (среднее по столбцам) xj (j=1,2,...u), по mj параллельным опытам, где mj – число данных в столбце j:
для каждого уровня фактора (среднее по столбцам) xj (j=1,2,...u), по mj параллельным опытам, где mj – число данных в столбце j: ;
; по всем N опытам, т.е. по всем mj параллельным опытам на всех уровнях фактора xj (
по всем N опытам, т.е. по всем mj параллельным опытам на всех уровнях фактора xj ( ):
): ;
;
 ;
; .
.
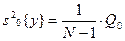 ,
, - число степеней свободы;
- число степеней свободы;
 .
.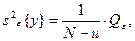


 , т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель. ,, т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.
,, т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель. .
. и числа степеней свободы сравниваемых дисперсий
и числа степеней свободы сравниваемых дисперсий 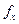 и
и  .
.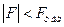 , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.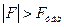 , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.


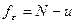


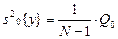
 - число данных в столбце, u- число столбцов, m – число строк.
- число данных в столбце, u- число столбцов, m – число строк.


