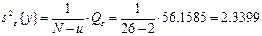Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Севастопольский национальный техническийСодержание книги
Поиск на нашем сайте Севастопольский национальный технический
университет
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторной работы № 3 и 4
” Дисперсионный анализ при помощи системы MINITAB для WINDOWS “ по учебной дисциплине “Прикладная статистика” для студентов экономических специальностей всех форм обучения
Севастополь
Методические указания рассмотрены и утверждены на заседании кафедры менеджмента и экономико -математических методов протокол № “_____” от “______________” 2008г.
Рецензент: доцент департамента учета и аудита Т.А.Мараховская
Цель работы Изучение возможностей дисперсионного анализа, для выявления зависимостей между экономическими показателями и получение практических навыков работы в системе MINITAB.
Теоретические сведения
Дисперсионный анализ Таблица 2 Однофакторный дисперсионный анализ
Двухфакторный дисперсионный анализ при перекрестной Классификации факторов Часто необходимо качественно оценить значимость или незначимость влияния на целевую функцию u двух одновременно действующих факторов x1 и x2. Такими факторами могут быть, например, форма собственности предприятия x1 и вид экономической деятельности x2. Модель двухфакторного дисперсионного анализа имеет вид [1-4]:
где В этом случае общую сумму квадратов отклонений Q0 можно разбить на четыре суммы: 1) Qx1-по фактору x1, 2) Qx2-по фактору x2, 3) Qe-остаточную сумму квадратов, зависящую от ошибки e, 4) Q x1x2-зависящую от взаимодействия (произведения) x1x2 двух факторов.
В этом случае по выборочным значениям вычисляются: 1) среднее
2) среднее
3) общее среднее
4) среднее
В табл.2 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках.
Таблица 3. - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе
В табл.2 Общая сумма квадратов отклонений Q0 рассчитывается по формуле:
Эту сумму можно разложить на 4 составляющие: 1) сумму, характеризующую влияние фактора x1:
2) сумму, характеризующую влияние фактора x2:
3) сумму, характеризующую результат влияния взаимодействия x1x2:
4) сумму, характеризующую влияние ошибки e:
Указанные пять сумм, поделенные на соответствующее число степеней свободы, дают пять различных оценок дисперсии, если влияние факторов x1 и x2 незначимо. Для проведения дисперсионного анализа вычисляются следующие дисперсии: 1) оценка дисперсии относительно общего среднего
где
2) оценка дисперсии «между строками», определяемыми уровнями x1j:
где 3) оценка дисперсии «между столбцами», соответствующими уровням фактора x2:
где 4) оценка дисперсии «между сериями» по m параллельным опытам каждая
с числом степеней свободы 5) оценка дисперсии «внутри серий» по m параллельным опытам, вычисляемая как средняя оценка по всем u1u2 сериям:
с числом степеней свободы Числа степеней свободы должны удовлетворять соотношению
Статистическое оценивание значимости влияния факторов x1, x2 и взаимодействия x1x2 выполняются по F-критерию Фишера, для чего формируются следующие F-отношения:
Фактор x1 или x2, или взаимодействие x1x2 признаются незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости Для того, чтобы сделать вывод о том, влияют ли на исследуемые показатели качественные факторы, выдвигают следующие гипотезы: H0: H1:
H0: H1:
H0: H1:
Если Если
Результаты двухфакторного дисперсионного анализа представляются в виде табл.3.
Таблица 3. - Двухфакторный дисперсионный анализ при равном числе наблюдений в ячейках
m – число данных в строке (число повторов в ячейке),
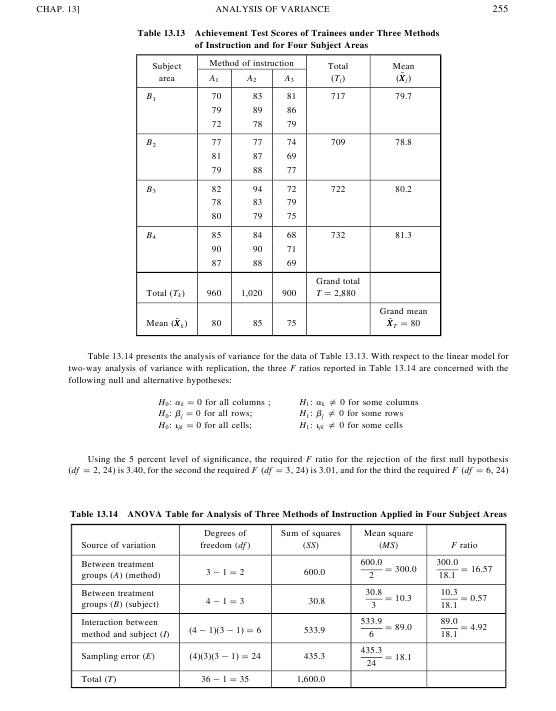
Пример 1 Пусть данные о проценте износа оборудования для 12 предприятий разных отраслей промышленности и форм собственности представлены следующей таблицей. Таблица 4. Исходные данные
Определим зависимость износа оборудования от отрасли промышленности. В этом случае в диалоговом окне указываются следующие значения Response: d Factor: field
Результаты дисперсионного анализа включают таблицу анализа дисперсии, таблицу средних значений уровней факторов, индивидуальные доверительные интервалы для каждого уровня и общее стандартное отклонение. На рис.1 представлен листинг результатов вычислений. На рисунке используются следующие обозначения: DF – число степеней свободы, SS - сумма квадратов, MS – средний квадрат, F - отношение Фишера, P - уровень значимости для вычисленного F, Level – уровень фактора, Mean – среднее значение, StDev – стандартное отклонение.
Пример 2 Пусть данные о проценте износа оборудования для 12 предприятий двух отраслей промышленности (пищевая - field1, машиностроение - field2) представлены в табл.5.
Таблица 5. Исходные данные
В этом случае в диалоговом окне указываются следующие значения. Responses [in separate columns]: field1 field2
Результатом дисперсионного анализа будет таблица представленная на рис.2.
Пример 3 Пусть данные о проценте износа оборудования для 12 предприятий разных отраслей промышленности и форм собственности представлены в табл.1. Определим, как влияют отрасль промышленности, форма собственности и их взаимодействие на процент износа оборудование. Для этого выберем из меню Stat > ANOVA > Balanced ANOVA и заполним диалоговое окно следующим образом
Responses: d Model: field owner field*owner Результаты дисперсионного анализа представлены на рис.4.
Рис.4 Листинг результатов вычислений для двухфакторной модели Проанализируем полученные результатs/ Для фактора отрасли P> Для фактора формы собственности P>
Для анализа многофакторных моделей по несбалансированным данным необходимо выбрать из меню Stat > ANOVA > General Linear Model. 4 Выполнение дисперсионного анализа в Excel
Рассмотрим дисперсионный анализ на следующем примере: за месяц известны данные о выработке рабочего за время работы в первую и во вторую смены.
Таблица 2 - Исходные данные
Можно ли считать, что расхождение между уровнями выработки рабочего в первую и во вторую смены несущественно, т.е. можно ли считать, что генеральные средние в двух подгруппах одинаковы и, следовательно, выработка рабочего может быть охарактеризована общей средней.
Решение. Для того чтобы ответить на поставленные вопросы, рассчитаем среднюю выработку рабочих в каждой смене. Величина выработки в первую и вторую смены различна. Теперь возникает вопрос о том, насколько существенны эти расхождения, нужно проверить предположение о возможном влиянии сменности на выработку рабочих. Результаты расчетов сведены в таблицу 3.
Таблица 3 – Промежуточные расчеты для проведения дисперсионного анализа
Используя данные таблицы, рассчитаем Число степеней свободы для расчета внутригрупповой дисперсии равно (
Рассчитаем значение критерия Фишера по следующей формуле:
В соответствии с числом степеней свободы для расчета внутригрупповой и межгрупповой дисперсий (24 и 1) в таблице F-распределения для α=5% находим Fтабл = 4.26. При этом выдвигается две гипотезы. Нулевая гипотеза гласит о том, что различия выработки рабочего в первую и вторую смены несущественны. Альтернативная гипотеза: существуют существенные различия в значении выработки рабочего в первую и во вторую смены. Так как расчетное значение критерия Фишера значительно меньше табличного значения критерия Фишера, то гипотеза о несущественности различия выработки рабочего в первую и вторую смены не опровергается, т.е. сменность не оказывает влияния на уровень выработки рабочего. Для того, чтобы провести дисперсионный анализ в Excel, необходимо активировать команду «Анализ данных». Для этого проходится следующий путь: Сервис -> Надстройки -> Пакет анализа. После этого в меню «Сервис» появляется команда «Анализ данных» и выбирается команда «Однофакторный дисперсионный анализ». Далее необходимо заполнить окно «Однофакторный дисперсионный анализ»: «Входной интервал» - вводится ссылка на диапазон, содержащий анализируемые данные. Ссылка должна состоять не менее чем из двух смежных диапазонов данных, данные в которых расположены по строкам или столбцам. «Группирование» - установите переключатель в положение. По столбцам или По строкам в зависимости от расположения данных во входном диапазоне. «Метки в первой строке/Метки в первом столбце» - если первая строка исходного диапазона содержит названия столбцов, установите переключатель в положение Метки в первой строке. Если названия строк находятся в первом столбце входного диапазона, установите переключатель в положение Метки в первом столбце. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически. «Альфа» - введите уровень значимости, необходимый для оценки критических параметров F-статистики. Уровень альфа связан с вероятностью возникновения ошибки типа I (опровержение верной гипотезы). «Выходной диапазон» - введите ссылку на левую верхнюю ячейку выходного диапазона. Размеры выходной области будут рассчитаны автоматически, и соответствующее сообщение появится на экране в том случае, если выходной диапазон занимает место существующих данных или его размеры превышают размеры листа. «Новый лист» - установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя. «Новая книга» - установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге. Пример заполнения окна «Однофакторный дисперсионный анализ» представлен на рисунке 2.
Рисунок 2 – Пример заполнения окна «Однофакторный дисперсионный анализ»
Результаты расчетов однофакторного дисперсионного анализа представлены на рисунке 3.
Рисунок 3 – Результаты расчетов по однофакторному дисперсионному анализу
Интерпретация результатов: «Группы» - данные по выработке в первую и вторую смены. «Счет» - количество наблюдений в каждой из групп. «Сумма» - сумма элементов каждой из групп. «Среднее» - средняя выработка в каждой из групп. «Дисперсия» - рассчитывается дисперсия по каждой из групп; SS - сумма квадратов; df - число степеней свободы; MS – средний квадрат; F – расчетное значение отношения Фишера; P - уровень значимости для вычисленного F; F критическое – табличное значение отношения Фишера. Результаты расчетов аналогичны результатам, полученным при расчетах вручную. Пример заполнения окна «Однофакторный дисперсионный анализ» представлен на рисунке 2.
Рисунок 2 – Пример заполнения окна «Двухфакторный дисперсионный анализ»
Результаты расчетов двухфакторного дисперсионного анализа представлены на рисунке 3.
Рисунок 3 – Результаты расчетов по однофакторному дисперсионному анализу
Интерпретация результатов: SS - сумма квадратов; df - число степеней свободы; MS – средний квадрат; F – расчетное значение отношения Фишера; P - уровень значимости для вычисленного F; F критическое – табличное значение отношения Фишера.
Задание по выполнению лабораторной работы Результаты опроса
Требуется методом двухфакторного дисперсионного анализа оценить степень влияния изучаемых факторов на результирующий экономический показатель. Первоначально оценить модель без взаимодействия факторов, затем с взаимодействием. Сравнить результаты. Сделать выводы. Варианты заданий приведены в табл.8.
Таблица 8 Варианты заданий
Порядок выполнения работы 1. В соответствии с вариантом задания выполнить однофакторный дисперсионный анализ, сделать выводы, написать отчет. 2. В соответствии с вариантом задания выполнить двухфакторный дисперсионный анализ, сделать выводы, написать отчет.
Контрольные вопросы 1. Сформулируйте основную идею дисперсионного анализа, для решения каких задач он наиболее эффективен? 2. Что показывает F отношение Фишера? 3. Каковы основные теоретические предпосылки дисперсионный анализ? 4. Произведите разложение общей суммы квадратов отклонений на составляющие в однофакторном дисперсионном анализе. 5. Как получить оценки дисперсий из сумм квадратов отклонений? Как получаются необходимые числа степеней свободы? 6. Приведите свой пример двухфакторного дисперсионного анализа. 7. На какие суммы разлагается общая сумма квадратов отклонений в двухфакторном дисперсионном анализе? 8. Поясните схему двухфакторного дисперсионного анализа. 9. Чем отличается перекрестная классификация от иерархической классификации? 10. Чем отличаются сбалансированные данные?
Литература
1. Шеффе Г. Дисперсионный анализ. – М.: Наука. 1980.- 512с. 2. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы планирования эксперимента. Пер. с англ. – М.: Мир, 1981.-520с. 3. Дэниел К. Применение статистики в промышленном эксперименте.-М.:Мир, 1979.-300с. 4. Хикс Ч. Основные принципы планирования эксперимента.- М.:Мир, 1967.
Методические указания разработали: профессор, д.т.н. Цуканов А.В. и к.т.н., доцент, Русина Н.А.
Севастопольский национальный технический
университет
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторной работы № 3 и 4
” Дисперсионный анализ при помощи системы MINITAB для WINDOWS “ по учебной дисциплине “Прикладная статистика” для студентов экономических специальностей всех форм обучения
Севастополь
Методические указания рассмотрены и утверждены на заседании кафедры менеджмента и экономико -математических методов протокол № “_____” от “______________” 2008г.
Рецензент: доцент департамента учета и аудита Т.А.Мараховская
Цель работы Изучение возможностей дисперсионного анализа, для выявления зависимостей между экономическими показателями и получение практических навыков работы в системе MINITAB.
Теоретические сведения
Дисперсионный анализ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |







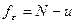



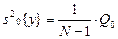
 - число данных в столбце, u- число столбцов, m – число строк.
- число данных в столбце, u- число столбцов, m – число строк.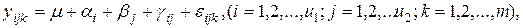
 - общее среднее,
- общее среднее,  -отклонение от общего среднего для фактора x1,
-отклонение от общего среднего для фактора x1,  - отклонение от общего среднего для фактора x2,
- отклонение от общего среднего для фактора x2,  - отклонение от общего среднего для взаимодействия двух факторов,
- отклонение от общего среднего для взаимодействия двух факторов,  - случайная составляющая.
- случайная составляющая.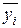 для каждого уровня фактора x1:
для каждого уровня фактора x1: ;
;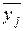 для каждого уровня фактора x2:
для каждого уровня фактора x2: ;
;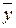 по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (
по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (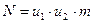 ):
): ;
; по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
по m параллельным опытам для каждого сочетания уровней факторов x1 и x2: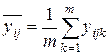 .
.
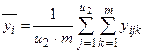
 i =
i =
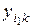


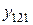
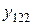
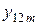


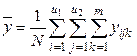
 вычисляется по выделенной части столбца, содержащей m параллельных опытов.
вычисляется по выделенной части столбца, содержащей m параллельных опытов.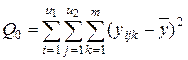
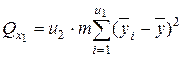 ;
;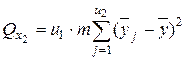 ;
;
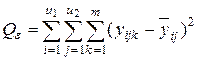
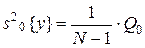 ,
, -общее число наблюдений, а число степеней свободы
-общее число наблюдений, а число степеней свободы ;
;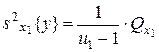 ,
,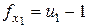 - число степеней свободы.
- число степеней свободы.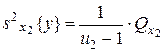 ,
, - число степеней свободы;
- число степеней свободы;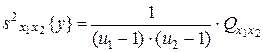
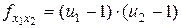 ;
;
 .
.
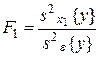 ,
, 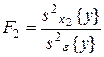 ,
, 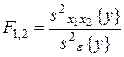 .
.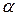 и числа степеней свободы сравниваемых дисперсий.
и числа степеней свободы сравниваемых дисперсий. , т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель. ,, т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
,, т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель. , т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..
, т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..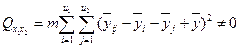 , фактор взаимодействия значим..
, фактор взаимодействия значим..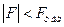 , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.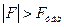 , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
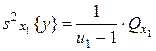
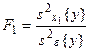
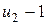
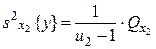
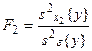
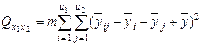
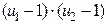

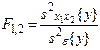
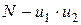
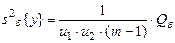

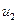 - число столбцов,
- число столбцов, 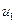 - число строк.
- число строк. (
(
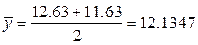
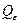 =56.1585
=56.1585
 =6,4008
=6,4008
 и
и 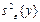 .
.