
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухфакторный дисперсионный анализ при перекрестнойСодержание книги
Поиск на нашем сайте
Классификации факторов Часто необходимо качественно оценить значимость или незначимость влияния на целевую функцию u двух одновременно действующих факторов x1 и x2. Такими факторами могут быть, например, форма собственности предприятия x1 и вид экономической деятельности x2. Модель двухфакторного дисперсионного анализа имеет вид [1-4]:
где В этом случае общую сумму квадратов отклонений Q0 можно разбить на четыре суммы: 1) Qx1-по фактору x1, 2) Qx2-по фактору x2, 3) Qe-остаточную сумму квадратов, зависящую от ошибки e, 4) Q x1x2-зависящую от взаимодействия (произведения) x1x2 двух факторов.
В этом случае по выборочным значениям вычисляются: 1) среднее
2) среднее
3) общее среднее
4) среднее
В табл.2 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках.
Таблица 3. - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе
В табл.2 Общая сумма квадратов отклонений Q0 рассчитывается по формуле:
Эту сумму можно разложить на 4 составляющие: 1) сумму, характеризующую влияние фактора x1:
2) сумму, характеризующую влияние фактора x2:
3) сумму, характеризующую результат влияния взаимодействия x1x2:
4) сумму, характеризующую влияние ошибки e:
Указанные пять сумм, поделенные на соответствующее число степеней свободы, дают пять различных оценок дисперсии, если влияние факторов x1 и x2 незначимо. Для проведения дисперсионного анализа вычисляются следующие дисперсии: 1) оценка дисперсии относительно общего среднего
где
2) оценка дисперсии «между строками», определяемыми уровнями x1j:
где 3) оценка дисперсии «между столбцами», соответствующими уровням фактора x2:
где 4) оценка дисперсии «между сериями» по m параллельным опытам каждая
с числом степеней свободы 5) оценка дисперсии «внутри серий» по m параллельным опытам, вычисляемая как средняя оценка по всем u1u2 сериям:
с числом степеней свободы Числа степеней свободы должны удовлетворять соотношению
Статистическое оценивание значимости влияния факторов x1, x2 и взаимодействия x1x2 выполняются по F-критерию Фишера, для чего формируются следующие F-отношения:
Фактор x1 или x2, или взаимодействие x1x2 признаются незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости Для того, чтобы сделать вывод о том, влияют ли на исследуемые показатели качественные факторы, выдвигают следующие гипотезы: H0: H1:
H0: H1:
H0: H1:
Если Если
Результаты двухфакторного дисперсионного анализа представляются в виде табл.3.
Таблица 3. - Двухфакторный дисперсионный анализ при равном числе наблюдений в ячейках
m – число данных в строке (число повторов в ячейке),
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.160.29 (0.01 с.) |

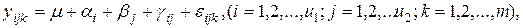
 - общее среднее,
- общее среднее,  -отклонение от общего среднего для фактора x1,
-отклонение от общего среднего для фактора x1,  - отклонение от общего среднего для фактора x2,
- отклонение от общего среднего для фактора x2,  - отклонение от общего среднего для взаимодействия двух факторов,
- отклонение от общего среднего для взаимодействия двух факторов,  - случайная составляющая.
- случайная составляющая.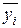 для каждого уровня фактора x1:
для каждого уровня фактора x1: ;
;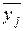 для каждого уровня фактора x2:
для каждого уровня фактора x2: ;
;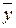 по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (
по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (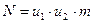 ):
): ;
; по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
по m параллельным опытам для каждого сочетания уровней факторов x1 и x2: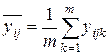 .
.
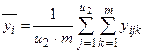
 i =
i =
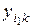


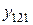
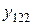
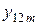


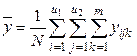
 вычисляется по выделенной части столбца, содержащей m параллельных опытов.
вычисляется по выделенной части столбца, содержащей m параллельных опытов.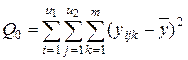
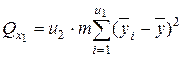 ;
;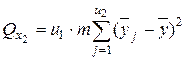 ;
;
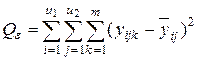
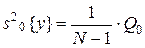 ,
, -общее число наблюдений, а число степеней свободы
-общее число наблюдений, а число степеней свободы ;
;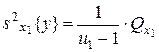 ,
,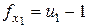 - число степеней свободы.
- число степеней свободы.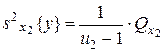 ,
, - число степеней свободы;
- число степеней свободы;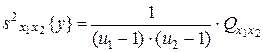
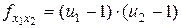 ;
;
 .
.
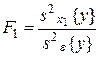 ,
, 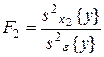 ,
, 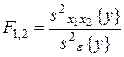 .
.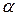 и числа степеней свободы сравниваемых дисперсий.
и числа степеней свободы сравниваемых дисперсий. , т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель. ,, т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
,, т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель. , т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..
, т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..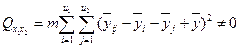 , фактор взаимодействия значим..
, фактор взаимодействия значим..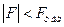 , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.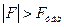 , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
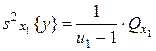
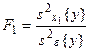
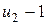
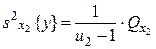
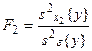
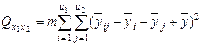
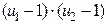

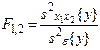
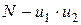
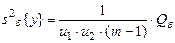

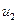 - число столбцов,
- число столбцов, 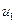 - число строк.
- число строк.


