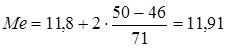Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое представление статистических рядовСодержание книги
Поиск на нашем сайте Для случая, когда количественный признак является дискретной величиной, его значения хi и соответствующие им частоты ni или относительные частоты wi представляют в виде таблицы, в которой значения признака (варианты) располагаются в порядке возрастания.
Такие таблицы называют статистическим дискретным рядом распределения или дискретным вариационным рядом.
Графически статистические ряды могут быть представлены в виде полигона, гистограммы или графика накопленных частот. Полигоном частот называют ломаную линию, отрезки которой соединяют точки (xi, ni). Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки (xi, Полигоны обычно служат для изображения выборки в случае дискретной случайной величины. Пример. В результате измерения температуры у 12 животных получены следующие значения: 37,8; 37,8; 38; 37,7; 37,9; 37,8; 37,5; 37,7; 37,6; 38; 38,1; 37,9. Требуется построить вариационный ряд и соответствующий ему полигон. Решение. Проанализируем исходные данные. Значение температуры t = 37,8 у животных наблюдалось три раза; значение температур t = 37,7; t = 37,9; t = 38 — по два раза; значение температур t = 37,5; t = 37,6; t = 38,1 — по одному разу. Исходя из этого, строим вариационный ряд:
Ему соответствует полигон частот(рис. 9)
Рис. 9 Полигон частот В случае большого количества вариантов и непрерывного распределения признака статистическое распределение признака можно задать в виде последовательности интервалов и соответствующих им частот или относительных частот. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на определенное количество частных интервалов (x0; x1]; (x1; x2]; …; (xk-1; xk] длиной h и находят для каждого частичного интервала сумму частот вариант Для графического изображения интервального ряда распределения используют гистограммы. Гистограмма относительных частот (или просто гистограмма) - ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длинною h, а высоты равны f*=
К=1+3,32ּlg(n) - количество классов (интервалов) Пример. У 30 коров измеряли окружность локтевого сустава. Получены следующие результаты измерений:
Для нашего примера
Рис. 10 Гистограмма плотности относительных частот Гистограмму можно рассматривать как график эмпирической (выборочной) плотности распределения fi (x). Если у теоретического распределения F существует конечная плотность, то эмпирическая плотность является некоторым приближением для теоретической. В этом и состоит практическая польза гистограммы. Графиком накопленных частот называется фигура, строящаяся аналогично гистограмме с той разницей, что для расчета высот прямоугольников берутся не простые, а накопленные относительные частоты, т.е. График эмпирической функции распределения проходит через правые верхние углы прямоугольника. График накопленных частот и эмпирическая функция распределения на практике используется для приближения теоретической функции распределения. Пример: Дан сгруппированный ряд наблюдений
Требуется построить гистограмму и график накопленных частот.
Рис.11. Гистограмма относительных частот.
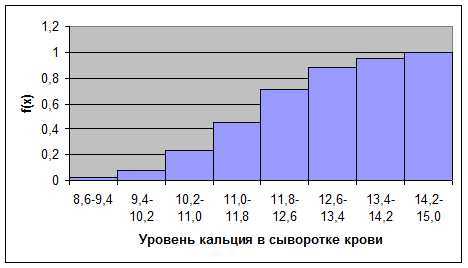
Рис.12. График накопленных частот (кумулята) Выборочные характеристики Средние величины Для того, чтобы количественно охарактеризовать самые существенные свойства распределения, а также для того, чтобы можно было сравнить разные распределения, вычисляют средние показатели - выборочные числовые характеристики. В статистике используются различные величины в зависимости от того, какие цели при анализе материала ставит исследователь. Понятием средней величины пользуемся в тех случаях, когда требуется определить средний надой по стаду, средний привес, средний прирост стада, средние клинические показатели деятельности сердца, лёгких, среднего состава крови и во многих других случаях. Различают следующие виды средних величин: средняя арифметическая ( Наиболее распространенным видом средних величин является средняя арифметическая, которая бывает простой и взвешенной. Возможны следующие случаи: 1. Результаты наблюдения не сведены в вариационный ряд или все частоты равны единице или одинаковы. Тогда вычисляют простую среднюю арифметическую
где хi – значение признака n – объём результатов (число наблюдений). 2. Частоты ni отличны друг от друга, то есть значения признака хi повторяются. В этом случае вычисляют среднюю арифметическую взвешенную (выборочную среднею)
3. Распределение интервальное. В этом случае вместо хi берут середину интервалов
Основные свойства среднего: 1)выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0; 2)сумма квадратов расстояний между наблюдаемыми значениями и их средним арифметическим является минимальным. Медиана выборки (термин был впервые введен Гальтоном, 1882) Медиана – это значение варианта, который делит ранжированный ряд на равные по числу вариант части. 4 7 12 8 9 5 7 13 15 Ме = 12 Ме = Свойство: сумма абсолютных расстояний между точками выборки и медианой минимальна. Если признак Х представлен интервально: медианному интервалу соответствует первая накопленная частота превосходящая n/2.
где
Модой (термин впервые введен Пирсоном,1894) называется вариант, имеющий наибольшую частоту. Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика») Мультимодальность распределения дает важную информацию о природе исследуемой переменной. Например, в социологических опросах, если переменная представляет собой предпочтения или отношение к чему-то, то мультимодальность может означать, что существует несколько определенно различных мнений. Мультимодальность так же служит индикатором того, что выборка не является однородной и наблюдения, возможно порождены двумя или более «наложенными» распределениями. Класс с наибольшей частотой называется модальным. Для определения моды интервальных рядов служит формула
где
Пример: На основании многолетних клинических наблюдений, проводившихся в Сухумском питомнике обезьян, составлена следующая выборка, включающая 100 анализов на содержание кальция (мг %) в сыворотке крови низших обезьян (павианов-гамадрилов).В данном случае признак варьирует непрерывно в пределах от 9,0 до 14,7 мг %. Задание: 1) составить интервальный вариационный ряд; 2) найти Мо, Ме; 3) построить график накопленных частот (кумуляту) Решение. 1) Установим величину классового интервала:
Определим нижнюю границу первого класса:
Составим классовые интервалы:
Получилось 8 интервалов. 2) Строим вспомогательную таблицу и разносим все 100 вариаций по намеченным классовым интервалам.
Модальный интервал 11,8-12,6, т.к. ему соответствует наибольшая частота n=25. По формуле для моды интервального вариационного ряда имеем
Медианному интервалу соответствует первая накопленная частота, превосходящая
3) График накопленных частот
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

 , где ni - это число повторений варианта
, где ni - это число повторений варианта i)
i)
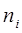 .
. i /h (или
i /h (или  -плотность относительных частот.
-плотность относительных частот.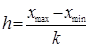 - длина соответствующего интервала
- длина соответствующего интервала


 . Данному вариационному ряду будет соответствовать гистограмма (рис. 10)
. Данному вариационному ряду будет соответствовать гистограмма (рис. 10)
 . Эти величины не убывают, и таким образом график накопленных частот имеет вид ступенчатой “лестницы” (от 0 до 1).
. Эти величины не убывают, и таким образом график накопленных частот имеет вид ступенчатой “лестницы” (от 0 до 1).


 ), средняя геометрическая (
), средняя геометрическая ( ), средняя квадратическая (
), средняя квадратическая ( ), средняя гармоническая (
), средняя гармоническая ( ), мода (М0) и медиана Ме.
), мода (М0) и медиана Ме. ,
,


 ,
, - нижняя граница медианного интервала
- нижняя граница медианного интервала – шаг разбиения, ширина класса
– шаг разбиения, ширина класса – накопленная частота интервала, предшествующего медианному интервалу
– накопленная частота интервала, предшествующего медианному интервалу - абсолютная частота медианного интервала.
- абсолютная частота медианного интервала.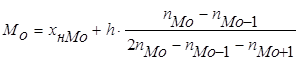 ,
, - нижняя граница модального интервала
- нижняя граница модального интервала – абсолютная частота модального интервала
– абсолютная частота модального интервала – абсолютная частота интервала, предшествующего модальному
– абсолютная частота интервала, предшествующего модальному – абсолютная частота интервала, следующего за модальным.
– абсолютная частота интервала, следующего за модальным.


 мг %
мг %





 (50).
(50).  . Следовательно, медианный интервал 11,8-12,6. По формуле для медианы интервального вариационного ряда имеем
. Следовательно, медианный интервал 11,8-12,6. По формуле для медианы интервального вариационного ряда имеем