
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Решение задач. Вычисление пределов функций.Содержание книги
Поиск на нашем сайте
Краткая теория темы. Опр. Пусть функция f(x) определена в некоторой окрестности точки «а». Число В называется пределом функции f(x) в точке «а» (или при x стремящемся к «а»), если для каждого В этом случае пишут: Некоторые предельные равенства. 1. 2. Теорема № 1: Для предела функции в точке верны следующие свойства: 1. 2. 3. 4. Правило № 1: Для раскрытия неопределенности Пример: Вычислить предел: 1. Здесь применили последовательно свойства из теоремы № 1, № 3 и №2, а также использовали № 2 и № 1. 2. Здесь имеется неопределенность Опр. Пусть функция f(x) определена на всей числовой прямой. Число В называется пределом функции f(x) при Опр. Функция f(x) называется бесконечно большой при Пример: 1. Функция 2. Функция Теорема № 2: Для предела функции на бесконечности выполняются следующие свойства: 1. 2. 3. Правило №2: Для раскрытия неопределенности Пример: Вычислить предел: 1.
Здесь имеется неопределенность Задания для решения. 1. Вычислить предел функции: 1) 4) 7) 10) 13) 16) Дополнительные задания. 1. Вычислить предел функции:
1) 4) 7) 10) Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Выполняются два примера задания.
Контрольные вопросы 1. Сформулируйте определение предела функции в точке. 2. Назовите основные предельные равенства. 3. Назовите правило раскрытия неопределенности 4. Сформулируйте определение предела функции на бесконечности. 5. Назовите правило раскрытия неопределенности 6. Сформулируйте основные свойства предела функции в точке и на бесконечности.
Инструкционная карта № 3. Практическое занятие № 3 по теме «Производная». Тема: Вычисление производных. Краткая теория темы. Опр. Производной функции Таблица производных функций.
Теорема №1: Если функция Пример: 1. Вычислить производную функции
Для вычисления производной данной функции последовательно воспользуемся формулами № 20, 1, 4, 7, 8, 13,11 таблицы, получим:
2. Вычислить производную сложной функции
Для вычисления производной сложной функции обозначим выражение, стоящее в скобках, другой переменной, например, t. Получим
По теореме №1 найдём производную функции
Здесь использовали формулу № 22 из таблицы производных – производная частного. Задания для решения. 1. Вычислить производную функции: 1) 4) 7) 10) 13) 2. Найти производную сложной функции: 1) 4) 7) 10)
13) Дополнительные задания. 1. Вычислить производную функции: 1) 4) 7) 10) 13) 2. Найти производную сложной функции: 1) 4) 7) 10) Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Первая цифра относится к первому заданию, а вторая – ко второму.
Контрольные вопросы 1. Дайте определение производной. 2. Сформулируйте теорему о нахождении производной сложной функции. Инструкционная карта № 4. Практическое занятие № 4 по теме «Интеграл».
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 913; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.180.253 (0.007 с.) |

 найдется такое число
найдется такое число  , что для всех х, удовлетворяющих неравенству
, что для всех х, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. .
. ,где с=const (т.е. некоторое постоянное число).
,где с=const (т.е. некоторое постоянное число). .
. .
. .
.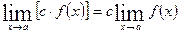 .
.
 надо разложить и числитель и знаменатель на множители и сократить на общий множитель, который обращает в нуль знаменатель и числитель дроби.
надо разложить и числитель и знаменатель на множители и сократить на общий множитель, который обращает в нуль знаменатель и числитель дроби.


 . Получили, что и в числителе, и в знаменателе имеется множитель
. Получили, что и в числителе, и в знаменателе имеется множитель  , сократим на него дробь. Далее применяем первое свойство теоремы № 1 и первое и второе предельные равенства.
, сократим на него дробь. Далее применяем первое свойство теоремы № 1 и первое и второе предельные равенства. , если для каждого
, если для каждого 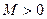 , что для х, удовлетворяющих условию
, что для х, удовлетворяющих условию  , имеет место неравенство
, имеет место неравенство  .
. ,если соответственно
,если соответственно  . Функция f(x) называется бесконечно малой при
. Функция f(x) называется бесконечно малой при  .
. является бесконечно большой при
является бесконечно большой при  .
. является бесконечно большой при
является бесконечно большой при  .
. .
.
 надо и числитель и знаменатель дроби разделить на х в старшей степени.
надо и числитель и знаменатель дроби разделить на х в старшей степени.
 ). Далее применяем одновременно третье и первое свойство теоремы № 2, а также определение бесконечно малой функции.
). Далее применяем одновременно третье и первое свойство теоремы № 2, а также определение бесконечно малой функции. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12)  ;
; ; 14)
; 14)  ; 15)
; 15)  ;
; ; 17)
; 17)  ; 18т)
; 18т)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12) 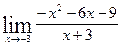 .
. по аргументу
по аргументу  называется предел отношения ее приращения
называется предел отношения ее приращения  к приращению
к приращению  аргумента
аргумента 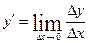 . Часто для обозначения производной используется символ
. Часто для обозначения производной используется символ  (читается «де эф по де икс»), т.е.
(читается «де эф по де икс»), т.е. 












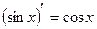



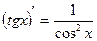




 , где U и V – некоторые функции
, где U и V – некоторые функции
 имеет производную в точке
имеет производную в точке  , а функция
, а функция  , то сложная функция
, то сложная функция  имеет производную в точке
имеет производную в точке 
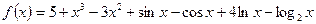


 .
.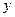 по переменной
по переменной 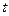 и функции
и функции 
 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9) 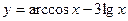 ;
; ; 11)
; 11) 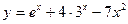 ; 12)
; 12)  ;
;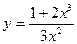 ; 14)
; 14)  ; 15)
; 15)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8) 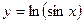 ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12)  ;
; ; 14)
; 14)  ; 15)
; 15)  .
. ; 2)
; 2)  ; 3)
; 3) 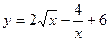 ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8) 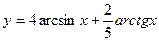 ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12)  ;
; ; 14)
; 14)  ; 15)
; 15)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8) 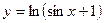 ; 9)
; 9)  ;
;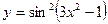 ; 11)
; 11)  ; 12)
; 12)  ;
;


