
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выполнение операций над множествами.Содержание книги
Поиск на нашем сайте
Инструкционная карта № 1. Практическое занятие № 1 по теме «Множества. Операции над множествами». Тема: Решение задач. Выполнение операций над множествами. Краткая теория темы. Опр. Множество – это совокупность предметов, объединенных по какому-либо признаку и рассматриваемых как единое целое. Обозначение: А, В, С… Опр. Предметы, из которых состоит множество, называются его элементами. Обозначение: a,b,c… А={a,b,c}, B={1,2,3} – примеры множеств. Опр. Объединением двух множеств А и В называется множество, состоящее из всех элементов множеств А и В и только из них. Обозначение: Пример: Найти объединение множеств А и В, если А={1,2,3}, B={3,4,5}. Опр. Пересечением двух множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат одновременно каждому из множеств А и В. Обозначение: Пример: Найти пересечение множеств А и В, если А={1,2,3}, B={3,4,5}.
Опр. Разностью множеств А и В называется множество, элементами которого являются элементы множества А, не принадлежащие множеству В. Обозначение: Пример: Найти разность множеств А и В, если А={1,2,3}, B={3,4,5}.
Опр. Прямым произведением множеств А и В называется множество всех упорядоченных пар, в которых первый элемент принадлежит множеству А, а второй элемент – множеству В. Обозначение: Пример: Найти прямое произведение множеств А и В, если А={1,2,3}, B={3,4,5}.
Опр. Если множества А и В совпадают, то прямое произведение этих множеств называется декартовым квадратом. Обозначение: Пример: Определить декартов квадрат множества А={1,2,3}.
Задания для решения.
1. Прочитать следующие записи: 2. Найти объединение множеств А и В, если 1) А={-3,0,3,6}, B={-3,-2,-1}; 2) A={-5,-3,-1}, B={-3,-1}; 3) A={2,4,6,8}, B={-2,0,2,4,6,8}; 4) A={2,4,6,8}, B={1,2,3,4,5,6,7,8}. 3. Найти пересечение множеств C и D, если 1) С={1,3,5,7,9}, B={3,5,7}; 2) C={-5,-3,-1}, B={-1,0,1}; 3) C={-2,0,2,4}, B={1,2,3}; 4) C={3,4,5,6}, B={0,1,2}. 4. Найти разность множеств K и L, если 1) K={1,2,3,4}, L={3,4}; 2) K={-2,-1,0,1,2,3}, L={-2,-1,0}; 3) K={-10,-5,0,5,10}, L={5}; 4) K={4,8,16}, L={1,2,3}. 5. Найти прямое произведение множеств P и Q, если 1) P={2,3}, Q={1,5,9}; 2) P={0,3,6,9}, Q={9}; 3) P={-1,1,3}, {2,3,4} 4) P={4,6}, Q={6,8,10,12}. 6. Найти декартов квадрат множеств A, B, C, D, если 1) А={7,9,11}; 2) B={4,10}; 3) C={-3,3,6,9};
4) D={-4,-3,-2}. 7. Найти объединение, пересечение, разность множеств А и В, если 1) А={-1,0,3,4}, B={0,4,6}; 2) A={2,5,7,9}, B={2,4,7}; 3) A=[0,2], B=[1,5]; 4) A=[-1,2], B=[0,4]. 8. Найти объединение, пересечение, разность, прямое произведение множеств А и В, декартов квадрат множества А, если 1) A={7,8,9}, B={8,9}; 2) A={1,2}, B={1,2,3,4}; 3) A={1,2}, B={3,4}; 4) A={3,5}, B={3,5,7}. 9. Пусть А={-4,-3,-2,-1,0,1,2}, B={-2,-1,0,1,2,3,4}, C={-4,-3,-2,-1,0,1,2,3,4}. Найдите множества: 10. Пусть N={0,1,2,3…} – множество натуральных чисел, Z={…-3,-2,-1,0, 1,2,3…} – множество целых чисел, а множества А, В, С определены в упражнении №4. Найдите множества: 11. В круг вписан квадрат. Пусть А – множество точек данного круга, В – множество точек квадрата. Найдите объединение, пересечение, разность этих множеств. Дополнительные задания. 1. Найти объединение, пересечение, разность, прямое произведение множеств А и В, декартов квадрат множества А, если
1) А={1,3,5}, B={3,5,7}; 2) A={2,3,4}, B={4,5,6}; 3) A={2,4,6}, B={2,8,10}; 4) A={3,4,6}, B={5,6,7}; 5) A={4,6,8}, B={7,8,9}; 6) A={1,4,9}, B={4,5,6}; 7) A={6,7,8}, B={7,8,9}; 8) A={6,8,10}, B={7,8,9}; 9) A={4,7,9}, B={6,7,8}; 10) A={3,7,9}, B={4,5,6}. Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Выполняются два примера задания.
Контрольные вопросы 1. Дайте определение множества. 2. Дайте определение элементов множества. 3. Какие операции можно осуществлять над множествами? 4. Сформулируйте определение объединения множеств. 5. Дайте определение пересечения множеств. 6. Дайте определение разности множеств. 7. Сформулируйте определение прямого произведения множеств. 8. Дайте определение декартова квадрата. Инструкционная карта № 3. Практическое занятие № 2 по теме «Функция. Предел функции». Задания для решения. 1. Вычислить предел функции: 1) 4) 7) 10) 13) 16) Дополнительные задания. 1. Вычислить предел функции:
1) 4) 7) 10) Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Выполняются два примера задания.
Контрольные вопросы 1. Сформулируйте определение предела функции в точке. 2. Назовите основные предельные равенства. 3. Назовите правило раскрытия неопределенности 4. Сформулируйте определение предела функции на бесконечности. 5. Назовите правило раскрытия неопределенности 6. Сформулируйте основные свойства предела функции в точке и на бесконечности.
Инструкционная карта № 3. Практическое занятие № 3 по теме «Производная». Таблица производных функций.
Теорема №1: Если функция Пример: 1. Вычислить производную функции
Для вычисления производной данной функции последовательно воспользуемся формулами № 20, 1, 4, 7, 8, 13,11 таблицы, получим:
2. Вычислить производную сложной функции
Для вычисления производной сложной функции обозначим выражение, стоящее в скобках, другой переменной, например, t. Получим
По теореме №1 найдём производную функции
Здесь использовали формулу № 22 из таблицы производных – производная частного. Задания для решения. 1. Вычислить производную функции: 1) 4) 7) 10) 13) 2. Найти производную сложной функции: 1) 4) 7) 10)
13) Дополнительные задания. 1. Вычислить производную функции: 1) 4) 7) 10) 13) 2. Найти производную сложной функции: 1) 4) 7) 10) Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Первая цифра относится к первому заданию, а вторая – ко второму.
Контрольные вопросы 1. Дайте определение производной. 2. Сформулируйте теорему о нахождении производной сложной функции. Инструкционная карта № 4. Практическое занятие № 4 по теме «Интеграл». Таблица неопределенных интегралов.
Пример: 1. Найти интеграл: Здесь применили свойства № 4 и №5 (т.е. интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов; и постоянный множитель можно вынести из под знака интеграла), а также формулы таблицы № 10, № 2, № 4, №5 и №13. 3. Вычислить интеграл:
Здесь применили свойства № 6 и № 7 (т.е. интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов; и постоянный множитель можно вынести из под знака интеграла), формулы таблицы № 4 и № 3, а также определение определённого интеграла. Задания для решения.
1. Найти неопределенный интеграл: 1. 7. 10. 14. 18. 22. 2. Вычислить определённый интеграл: 1. 7. 11. 15. Дополнительные задания. 1. Рассчитать неопределённый интеграл: 1. 7. 10. 14. 18. 2. Вычислить определённый интеграл: 1. 7. 11. 15. Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Первая цифра относится к первому заданию, а вторая – ко второму.
Контрольные вопросы 1. Сформулируйте определение первообразной, неопределенного интеграла, определенного интеграла. 2. Назовите свойства интегралов. Инструкционная карта № 5. Практическое занятие № 5 по теме «Дифференциальные уравнения». Задания для решения. 1. Решить дифференциальное уравнение первого порядка: 1. 6. 11. 15. 19. 23. 2. Решить дифференциальное уравнение второго порядка: 1. 5. 9. Дополнительные задания. 1. Решить дифференциальное уравнение первого порядка: 1. 6. 10. 14. 17. 20. 23.
2. Решить дифференциальное уравнение второго порядка: 1. 5. 9. Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Первая цифра относится к первому заданию, а вторая – ко второму.
Контрольные вопросы 1. Сформулируйте общее определение дифференциального уравнения. 2. Дайте определение дифференциального уравнения первого порядка. 3. Сформулируйте определение дифференциального уравнения второго порядка. 4. Дайте определение решения дифференциального уравнения. 5. Сформулируйте определение дифференциального уравнения с отделенными переменными. 6. Дайте определение дифференциального уравнения с отделяющимися переменными.
7. Сформулируйте план решения дифференциальных уравнений с отделенными переменными, с разделяющимися переменными, а также план решения дифференциальных уравнений второго порядка. Инструкционная карта № 6. Практическое занятие № 6 по теме «Элементы теории вероятностей». Задания для решения. 1. Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Какова вероятность того, что номер набран правильно? 2. Две грани симметричного кубика окрашены в синий цвет, три – в зеленый и одна – в красный. Кубик подбрасывают один раз. Какова вероятность того, что верхняя грань окажется зеленой? 3. Какова вероятность того, что при однократном подбрасывании игрального кубика выпадет четное число очков? 4. На каждой из семи одинаковых карточек напечатана одна из следующих букв: «н», «о», «п», «р», «с», «т», «у». Найти вероятность того, что на пяти взятых наугад и расположенных в ряд карточках можно прочесть слово «спорт». 5. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки, складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: 1) четное; 2) нечетное; 3) составное; 4) однозначное; 5) двузначное. 6. Среди 100 электроламп 5 испорченных. Какова вероятность того, что выбранные на удачу 3 лампы окажутся исправными? 7. Из урны, в которой находятся 3 белых, 4 черных, 5 красных шаров, наудачу вынимается один. Какова вероятность того, что вынутый шар окажется: 1) белым; 2) черным; 3) желтым; 4) красным. 8. Бросаются две игральные кости. Какова вероятность того, что сумма очков, выпавших на двух костях, окажется равной 10? 9. В урне 4 белых и 7 черных шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара белые? 10. В лотерее из 50 билетов 8 выигрышных. Какова вероятность того, что среди первых пяти наугад выбранных билетов два будут выигрышными? 11. В партии из 12 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наугад деталей 4 стандартных. 12. Из урны, содержащей 6 шаров, пронумерованных цифрами от 1 до 6, наугад вынимают один за другим все шары. Какова вероятность того, что шары будут вынуты в порядке возрастания их номеров? Дополнительные задания. 1. В забеге участвуют пять спортсменов: А, Б, В, Г и Д, каждый из которых имеет одинаковые шансы на успех. Какова вероятность того, что первые три места займут соответственно бегуны А, Б и В? 2. Из восьми букв разрезной азбуки составлено слово «институт». Затем карточки с буквами перемешивают и вновь собирают в произвольном порядке. Какова вероятность того, что снова получится слово «институт»? 3. Слово «учебник» составлено из букв разрезной азбуки. Затем карточки с буквами перемешивают и из них извлекают по очереди 6 карточек. Какова вероятность того, что эти шесть карточек в порядке выхода составят слово «ученик»? 4. Трехзначное число образовано наугад выбранными тремя не повторяющимися цифрами из числа цифр 1, 2, 3, 4, 5. Какова вероятность того, что это число четное?
5. Из урны, содержащей 6 белых и 8 черных шаров, наугад вынимают два шара. Какова вероятность того, что вынутые шары одного цвета? 6. На полке лежат 12 учебников, из них 7 – по математике. Студент берет на удачу 5 учебников. Какова вероятность того, что взяты учебники по математике? 7. В партии из 100 деталей содержится пять бракованных. Какова вероятность того, что среди выбранных на удачу 50 изделий будет хотя бы одно бракованное? 8. Восемь шаров случайным образом размещаются по восьми ящикам. Найти вероятность того, что каждый ящик будет занят? 9. Автобус должен сделать 8 остановок. Найти вероятность того, что никакие два пассажира из пяти, едущих в автобусе, не выйдут на одной и той же остановке. 10. Из 15 билетов выигрышными являются четыре. Какова вероятность того, что среди шести билетов, взятых наудачу, будет два выигрышных? 11. В классе учится 15 мальчиков и 25 девочек. По жребию выбирают пять учеников этого класса. Какова вероятность того, что среди них окажется две девочки? 12. Монета подброшена два раза. Найти вероятность того, что хотя бы один раз появится цифра. Варианты заданий Выбор варианта осуществляется в соответствии с порядковым номером в списке журнала. Выполняются два примера задания.
|

 .
. .
. .
.
 .
.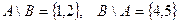 .
. .
. ,
, .
. .
. .
. где R- множество действительных чисел, P- множество рациональных чисел, N- множество натуральных чисел.
где R- множество действительных чисел, P- множество рациональных чисел, N- множество натуральных чисел.

 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12)  ;
; ; 14)
; 14)  ; 15)
; 15)  ;
; ; 17)
; 17)  ; 18т)
; 18т)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12) 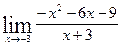 .
. .
. .
.











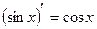



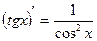




 , где U и V – некоторые функции
, где U и V – некоторые функции
 имеет производную в точке
имеет производную в точке  , а функция
, а функция  имеет производную в соответствующей точке
имеет производную в соответствующей точке  , то сложная функция
, то сложная функция  имеет производную в точке
имеет производную в точке 
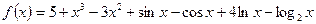


 .
.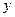 по переменной
по переменной  , как произведение производных функций
, как произведение производных функций 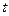 и функции
и функции 
 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9) 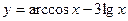 ;
; ; 11)
; 11) 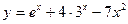 ; 12)
; 12)  ;
;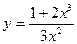 ; 14)
; 14)  ; 15)
; 15)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8) 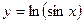 ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12)  ;
; ; 14)
; 14)  ; 15)
; 15)  .
. ; 2)
; 2)  ; 3)
; 3) 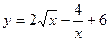 ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8) 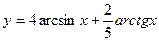 ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12)  ;
; ; 14)
; 14)  ; 15)
; 15)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8) 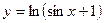 ; 9)
; 9)  ;
;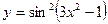 ; 11)
; 11)  ; 12)
; 12)  ;
;






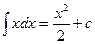







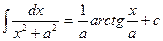







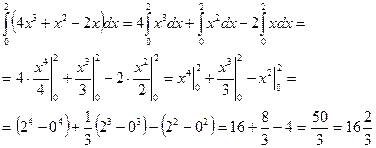
 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ;
; ; 8.
; 8.  ; 9.
; 9.  ;
;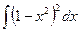 ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13.  ;
; ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17.  ;
; ; 19.
; 19. 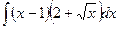 ; 20.
; 20. 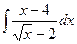 ; 21.
; 21.  ;
;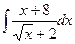 ; 23.
; 23. 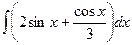 ; 24.
; 24.  .
. ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ;
; ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ;
; ; 12.
; 12.  ; 13.
; 13. 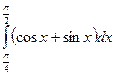 ; 14.
; 14.  ;
; ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19.  .
. ; 2.
; 2. 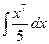 ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ;
; ; 8.
; 8. 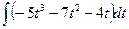 ; 9.
; 9.  ;
; ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13.  ;
; ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17. 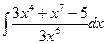 ;
; ; 19.
; 19.  ; 20.
; 20.  .
. ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5. 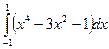 ;
; ; 8.
; 8. 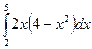 ; 9.
; 9.  ; 10.
; 10.  ;
; ; 12.
; 12.  ; 13.
; 13.  ; 14.
; 14.  ;
; ; 16.
; 16. 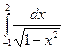 ; 17.
; 17.  ; 18.
; 18.  ; 19.
; 19.  .
.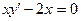 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ;
; ; 7.
; 7.  ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ;
; ; 12.
; 12.  ; 13.
; 13.  ; 14.
; 14.  ;
; ; 16.
; 16.  ; 17.
; 17.  ; 18.
; 18.  ;
; ; 20.
; 20.  ; 21.
; 21.  ; 22.
; 22.  ;
; ; 24.
; 24.  ; 25.
; 25. 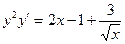 .
. ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4. 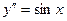 ;
;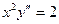 ; 6.
; 6.  ; 7.
; 7. 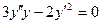 ; 8.
; 8.  ;
; ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  .
. ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5. 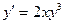 ;
; ; 7.
; 7.  ; 8.
; 8. 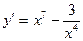 ; 9.
; 9. 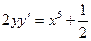 ;
; ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13. 
 ; 15.
; 15.  ; 16.
; 16.  ;
; ; 18.
; 18.  ; 19.
; 19.  ;
; ; 21.
; 21.  ; 22.
; 22.  ;
; ; 24.
; 24.  ; 25.
; 25.  .
. ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4. 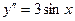 ;
; ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8. 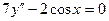 ;
; ; 10.
; 10. 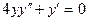 ; 11.
; 11.  ; 12.
; 12.  .
.


