
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие неопределенного интегралаСодержание книги
Поиск на нашем сайте
Глава II НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Понятие неопределенного интеграла
Дадим несколько первых вводных определений, более подробное изложение которых имеется в любом учебнике математического анализа (см. список рекомендуемой литературы в конце пособия). ИНТЕГРИРОВАНИЕ – одно из основных понятий математического анализа, обратное действию дифференцирования или вычислению производных. Так как в случае одной переменной дифференциал и производная связаны формулой df = f'dx, то вычисление дифференциала фактически сводится к вычислению производной. Действие, обратное вычислению производной, принято называть нахождением первообразной. Совокупность всех первообразных, соответствующих данной функции, и называется неопределенным интегралом. Перейдем к точным определениям. Всюду ниже под (a,b) понимается интервал, полупрямая или вся действительная ось. Определение 1. Пусть функция f(x) задана на (a,b) и существует дифференцируемая на (a,b) функция F(x), для которой всюду на (a,b) выполняется равенство F'(x) = f(x). Тогда функция F(x) называется первообразной для функции f(x) на (a,b). Определение 2. Совокупность всех первообразных на (a,b) для функции f(x) на (a,b) называется неопределенным интегралом от функции f(x) на (a,b) и обозначается В этом обозначении знак Оказывается, достаточно найти одну первообразную, чтобы описать всю совокупность первообразных или неопределенный интеграл. Корректность этого высказывания подтверждает нижеследующая теорема. Теорема 1. Любые две первообразные одной и той же функции отличаются на константу. ►Действительно, пусть F1 и F2- две первообразные одной функции f(x) и G = F1- F2 на (a,b). Тогда из определения 1 имеем G' = 0 всюду на (a,b). Поэтому из известной теоремы Лагранжа (теорема о среднем) вытекает G(z) - G(w) = =G'(s)(z-w), где точка s лежит между произвольными точками z и w, также лежащими на (a,b). Поэтому G(z) = G(w) или F1(z)- F2(z) = F1(w)- F2(w). Следовательно, F1(z)- F2(z) = С – const постоянна всюду на (a,b). Что и требовалось доказать. ◄ Таким образом,
Всегда ли существует первообразная? Или, иначе - любую ли функцию можно проинтегрировать? Конечно, не любую. Не вдаваясь в подробности, заметим лишь, что для непрерывных на отрезке функций неопределенный интеграл существует всегда. Желающих более подробно ознакомиться с вопросом существования отсылаем за справками к литературе см. [2, 17]. Тем не менее даже если и существует первообразная, она не всегда может выражаться через элементарные функции, такие как показательная, логарифмическая, синус, косинус и др. В том случае, когда первообразная выражается через основные элементарные функции, говорят, что интеграл берется в конечном виде или элементарных функциях. Часто используемым первообразным, которые не берутся в конечном виде, пришлось придумать новые названия. Например, функция si x:= Все основные элементарные функции в области, где они определены, конечно, интегрируемы. Прямо из определения получаем нижеследующую таблицу интегралов. Все результаты легко проверяются дифференцированием.
Минимальная таблица основных неопределенных интегралов 0. 1. 2. 3. 4. 10.
Эта таблица достаточно невелика, легка для запоминания и с ее помощью можно получить практически все интегралы от функций, берущихся в конечном виде. Желательно, чтобы читатель получил ее совершенно самостоятельно, опираясь на знание производных элементарных функций. Упражнение 1. Проверить минимальную таблицу интегралов дифференцированием.
Метод замены
Метод (правило) замены, или подстановки, является одновременно самым эффектным и эффективным методом интегрирования. Основу метода составляет следующее простое утверждение. Теорема 2. Пусть функция
►Достаточно опять воспользоваться правилом дифференцирования сложной функции Предположим теперь, что нам требуется вычислить интеграл Замечание. Теорема 2 остается справедливой если вместо (a,b) взять некоторое множество Х, представляющее из себя сегмент, полуинтервал или всю прямую. Естественно, тогда нужно заменить и интервал (a,b) на образ множества Х при отображении
В ряде случаев удается выбрать в качестве новой переменной такую дифференцируемую функцию Конечно, такой прием применим не ко всякому интегралу. Кроме того, следует подчеркнуть, что выбор правильной подстановки в значительной мере определяется искусством вычислителя, которое может прийти только с практикой. Рассмотрим несколько простых примеров (в прямых скобках указаны заменяемые функции и их дифференциалы). 1.
При получении определенного навыка это решение записывают так
-ln|cosx| +C. Этот прием называется внесением под знак дифференциала. Понятно, что это тот же метод замены, только роль переменной здесь играет cosx. Аналогично 2. Внесением под знак дифференциала решаются следующие два примера 3. 4. 5. В этом интеграле лучше сделать подстановку:
Перейдем теперь к переменной x, полагая
6. Здесь удобнее применить гиперболическую подстановку. Останавливаясь для примера, на нижнем знаке, положим:
Для перехода к x вспомним выражение обратной для гиперболического косинуса функции
причем в постоянную С мы включаем и слагаемое 7. В данном случае одинаково просто приводят к цели и тригонометрическая и гиперболическая подстановки. Для примера, во втором интеграле возьмем
8. Подстановка:
но
так что окончательно
В силу дальнейшего частого использования правила замены, мы не приводим более примеров на это правило, тем не менее читателю рекомендуется решить несколько закрепляющих примеров. Упражнение 4. Для каждого из 4-х приведенных ниже интегралов существует подстановка сводящая его к табличному. Укажите для каждого интеграла нужную подстановку
Интеграл от произвольной функции с помощью свойств и правил интегрирования сводят к рациональной функции. По схеме, изложенной в теореме 5, проводят интегрирование рациональной дроби. Этот прием и называется методом рационализации подынтегрального выражения. Можно рассматривать рациональные функции от двух переменных (вполне аналогично можно рассматривать рациональные функции от трех и более переменных). Определение 5. Рациональной функцией или рациональной дробью R(x,y) от двух переменных (x,y) называют отношение двух алгебраических полиномов
Так же, как и для одной переменной, множество рациональных дробей от двух переменных обладает рядом почти очевидных свойств.
Свойства рациональных дробей Глава II НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Понятие неопределенного интеграла
Дадим несколько первых вводных определений, более подробное изложение которых имеется в любом учебнике математического анализа (см. список рекомендуемой литературы в конце пособия).
ИНТЕГРИРОВАНИЕ – одно из основных понятий математического анализа, обратное действию дифференцирования или вычислению производных. Так как в случае одной переменной дифференциал и производная связаны формулой df = f'dx, то вычисление дифференциала фактически сводится к вычислению производной. Действие, обратное вычислению производной, принято называть нахождением первообразной. Совокупность всех первообразных, соответствующих данной функции, и называется неопределенным интегралом. Перейдем к точным определениям. Всюду ниже под (a,b) понимается интервал, полупрямая или вся действительная ось. Определение 1. Пусть функция f(x) задана на (a,b) и существует дифференцируемая на (a,b) функция F(x), для которой всюду на (a,b) выполняется равенство F'(x) = f(x). Тогда функция F(x) называется первообразной для функции f(x) на (a,b). Определение 2. Совокупность всех первообразных на (a,b) для функции f(x) на (a,b) называется неопределенным интегралом от функции f(x) на (a,b) и обозначается В этом обозначении знак Оказывается, достаточно найти одну первообразную, чтобы описать всю совокупность первообразных или неопределенный интеграл. Корректность этого высказывания подтверждает нижеследующая теорема. Теорема 1. Любые две первообразные одной и той же функции отличаются на константу. ►Действительно, пусть F1 и F2- две первообразные одной функции f(x) и G = F1- F2 на (a,b). Тогда из определения 1 имеем G' = 0 всюду на (a,b). Поэтому из известной теоремы Лагранжа (теорема о среднем) вытекает G(z) - G(w) = =G'(s)(z-w), где точка s лежит между произвольными точками z и w, также лежащими на (a,b). Поэтому G(z) = G(w) или F1(z)- F2(z) = F1(w)- F2(w). Следовательно, F1(z)- F2(z) = С – const постоянна всюду на (a,b). Что и требовалось доказать. ◄ Таким образом, Всегда ли существует первообразная? Или, иначе - любую ли функцию можно проинтегрировать? Конечно, не любую. Не вдаваясь в подробности, заметим лишь, что для непрерывных на отрезке функций неопределенный интеграл существует всегда. Желающих более подробно ознакомиться с вопросом существования отсылаем за справками к литературе см. [2, 17]. Тем не менее даже если и существует первообразная, она не всегда может выражаться через элементарные функции, такие как показательная, логарифмическая, синус, косинус и др. В том случае, когда первообразная выражается через основные элементарные функции, говорят, что интеграл берется в конечном виде или элементарных функциях. Часто используемым первообразным, которые не берутся в конечном виде, пришлось придумать новые названия. Например, функция
si x:= Все основные элементарные функции в области, где они определены, конечно, интегрируемы. Прямо из определения получаем нижеследующую таблицу интегралов. Все результаты легко проверяются дифференцированием.
Минимальная таблица основных неопределенных интегралов 0. 1. 2. 3. 4. 10.
Эта таблица достаточно невелика, легка для запоминания и с ее помощью можно получить практически все интегралы от функций, берущихся в конечном виде. Желательно, чтобы читатель получил ее совершенно самостоятельно, опираясь на знание производных элементарных функций. Упражнение 1. Проверить минимальную таблицу интегралов дифференцированием.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.182.126 (0.009 с.) |

 .
. называется знаком интеграла, выражение f(x)dx – подинтегральным выражением и f(x) - подынтегральной функцией. Читается: «интеграл от эф по дх».
называется знаком интеграла, выражение f(x)dx – подинтегральным выражением и f(x) - подынтегральной функцией. Читается: «интеграл от эф по дх». = F(x) + C, где С некоторая постоянная, а F(x)- некоторая первообразная для функции f(x). Поэтому достаточно найти только одну первообразную, чтобы вычислить неопределенный интеграл.
= F(x) + C, где С некоторая постоянная, а F(x)- некоторая первообразная для функции f(x). Поэтому достаточно найти только одну первообразную, чтобы вычислить неопределенный интеграл. называется интегральным синусом.
называется интегральным синусом. = C 5.
= C 5.  = ln
= ln  + C (x
+ C (x  0)
0) =xa+1/a+1 + C (a
=xa+1/a+1 + C (a 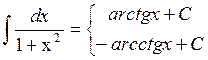
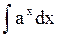 = ax/lna + C (0<a
= ax/lna + C (0<a 
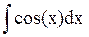 = sin(x) + C 8.
= sin(x) + C 8. 
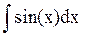 = - cos(x) + C 9.
= - cos(x) + C 9. 
 11.
11. 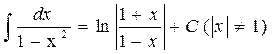 .
. определена и дифференцируема на (a,b) и
определена и дифференцируема на (a,b) и  на (a,b), причем a=j(a), b=j(b). Тогда
на (a,b), причем a=j(a), b=j(b). Тогда  .
. и учесть, что по определению первообразной G`(t) = g(t). Теорема 2 доказана. ◄
и учесть, что по определению первообразной G`(t) = g(t). Теорема 2 доказана. ◄ .
. и потребовать существование на этом образе первообразную G(t).
и потребовать существование на этом образе первообразную G(t). , что имеет место равенство
, что имеет место равенство  , причем функция g(t) легко интегрируется, т. е. интеграл
, причем функция g(t) легко интегрируется, т. е. интеграл  просто вычисляется. Доказанная выше теорема 2 позволяет написать нам равенство
просто вычисляется. Доказанная выше теорема 2 позволяет написать нам равенство  =
=  Этот прием вычисления интеграла и называется методом замены, или подстановки, переменной.
Этот прием вычисления интеграла и называется методом замены, или подстановки, переменной.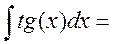

 =
=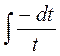 =-ln
=-ln  +C= -ln|cosx| +C.
+C= -ln|cosx| +C.



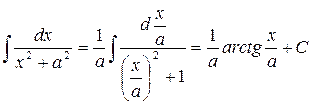 .
.
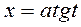 ,
,  ,
,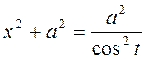 , так что
, так что .
. и выражая
и выражая  и
и  через
через  . Окончательно
. Окончательно .
.
 (при x и t>0),
(при x и t>0), . Интеграл приведется просто к
. Интеграл приведется просто к 
 ,
, .
. ,
,  ,
,  .
. , тогда
, тогда  и
и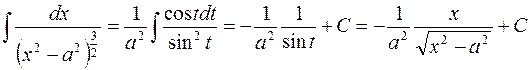

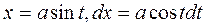 приводит этот интеграл к такому
приводит этот интеграл к такому ,
,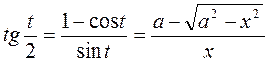 ,
, .
. ,
, .
. .
. .
. .
.


