
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование рациональных дробейСодержание книги
Поиск на нашем сайте
Как уже отмечалось выше, неопределенный интеграл от элементарных функций может не выражаться через элементарные функции, тем не менее, существуют широкие классы функций, неопределенные интегралы от которых выражаются через элементарные функции. Наиболее важным среди указанных классов функций является класс рациональных дробей, или рациональных функций. Определение 3. Рациональной функцией или рациональной дробью R(x) называют отношение двух алгебраических полиномов Pn(x) = anxn + an-1xn-1 +...+ a1x + a0 и Qm(x) = bmxm + bm-1xm-1 +...+ b1x + b0
Определение 4. Рациональная дробь называется правильной, если степень n многочлена Pn(x), стоящего в числителе меньше степени m многочлена Qm(x), стоящего в знаменателе. Самой простой рациональной функцией, или дробью, является многочлен. В этом случае знаменатель дроби Qm(x) равен 1. Неправильную рациональную дробь можно с помощью деления “столбиком” свести к правильной. Пример: Деление столбиком выглядит следующим образом:
Таким образом, неправильная рациональная дробь с помощью «деления стобиком» может быть представлена в виде суммы многочлена и правильной рациональной дроби. Так как многочлен легко интегрируется, то вопрос об интегрировании рациональных дробей сводится к интегрированию правильных рациональных дробей. Интегрирование правильной рациональной дроби с вещественными коэффициентами в свою очередь сводится к интегрированию следующих четырех простых рациональных дробей (иногда называемых элементарными): I. Причем у квадратного трехчлена Первые две элементарные рациональные дроби интегрировать особенно легко, опираясь на табличные интегралы №1 и №5 и правило интегрирования №5. 1. 2. Для интегрирования элементарных рациональных дробей третьего типа воспользуемся методом подстановки. Преобразуем знаменатель дроби III следующим образом:
Обозначим 3.
С интегралом IV типа вначале поступаем аналогично
Далее с первым из полученных интегралов поступаем опираясь на упражнение 4, а ко второму полученному интегралу применяем частный случай метода интегрирования по частям, – интегрирование рекуррентных соотношений. Этот интеграл вычислен выше (см § 4 с.65). Аналогичный интеграл рекомендуется найти читателю в качестве упражнения. Упражнение 7. Найти интеграл Итак, все четыре типа простых рациональных дробей интегрируются в элементарных функциях. Разложение правильной дроби на простые дроби теснейшим образом связано с разложением ее знаменателя Qm(x) на простые множители. Опираясь на основную теорему алгебры, доказывается теорема о разложении многочлена с вещественными коэффициентами на линейные множители типа (х-а) и квадратичные множители типа (х2 + px + q); при этом квадратичные множители предполагаются не имеющими вещественных корней и, следовательно, неразложимыми на вещественные линейные множители. Объединяя одинаковые множители (если таковые имеются) и полагая для простоты старший коэффициент многочлена Qm(x) равным единице, можно записать разложение этого многочлена схематически в виде Qm(x)=(x – a)k... (х2 + px + q)i..., где k,..., i,... - суть натуральные числа. Заметим, что если степень многочлена Qm(x) есть m, то, очевидно, сумма всех показателей k, сложенная с удвоенной суммой всех показателей i, в точности даст m
С помощью этого разложения получают разложение правильной рациональной дроби на простейшие. Приведем без доказательства теорему о разложении. Теорема 4. Пусть
причем многочлены х2 + pnx + qn (n = 1,2,...,i) не имеют вещественных корней, т. е. неразложимы на линейные множители. Тогда для этой дроби справедливо следующее разложение на сумму простейших дробей
В этом разложении – некоторые вещественные постоянные, часть из которых может быть равна нулю. Для определения упомянутых коэффициентов обычно пользуются методом неопределенных коэффициентов, который состоит в следующем. Зная форму разложения дроби P/Q, пишут его с буквенными коэффициентами в числителях справа. Общим знаменателем всех простых дробей разложения, очевидно, будет Q; складывая их, получим правильную дробь. Если отбросить теперь слева и справа знаменатель Q, то придем к равенству двух многочленов (m – 1) степени, тождественному относительно х. Коэффициентами при различных степенях многочлена справа будут линейные однородные многочлены относительно m коэффициентов, обозначенных буквами; приравнивая их к соответствующим численным коэффициентам многочлена Р, получим, наконец, систему mлинейных уравнений, из которых буквенные коэффициенты и определятся. Ввиду того, что возможность разложения на простые дроби наперед установлена, упомянутая система никогда не может оказаться противоречивой. Больше того, так как упомянутая система уравнений имеет решение, каков бы ни был набор свободных членов (коэффициентов многочлена Р, то ее определитель необходимо будет отличен от нуля. Иными словами, система всегда оказывается определенной. Это простое замечание попутно доказывает и единственность разложения правильной дроби на простые дроби. Рассмотрим пример. Пусть дана дробь
Согласно теореме 4, для нее имеется разложение
Коэффициенты A,B, С, D, Е определим, исходя из тождества 2х2+2х+13= А(х2+1) 2+(Вх+С)*(х2+1) *(х-2) + (Dx+E)* (х-2). Приравнивая коэффициенты при одинаковых степенях х слева и справа, придем к системе из пяти уравнений x4 | A+B=0 x3 | -2B+C=0 x2 | 2A+B-2C+D=2 x1 | -2B+C-2D+E=2 x0 | A-2C-2E=13 Решая систему, находим A = 1, B = –1, C = –2, D = –3, E = –4. Решению соответствует разложение
Алгебраический факт, который выражает теорема 4, имеет непосредственное применение к интегрированию рациональных дробей. Выше мы проинтегрировали простые дроби в элементарных функциях. Теперь мы то же самое можем сказать о любой рациональной дроби. Для этого случая имеем
Если внимательно всмотреться в те функции, через которые выражаются интегралы от целого многочлена и от элементарных дробей, то можно сформулировать более точный результат. Теорема 5. Интеграл от любой рациональной функции выражается в конечном виде – с помощью рациональной же функции, логарифма и арктангенса. ►Действительно, любую рациональную функцию мы можем представить в виде суммы алгебраического многочлена и правильной рациональной дроби. В свою очередь правильная рациональная дробь, на основании теоремы 4, может быть представлена в виде суммы элементарных рациональных дробей. Таким образом, любую рациональную функцию мы можем представить в виде суммы алгебраического многочлена и элементарных рациональных дробей. Следовательно, интеграл от рациональной функции, по свойству интегрирования № 3, распадается на сумму интегралов от алгебраического многочлена и элементарных рациональных дробей. Как было показано выше, алгебраический многочлен и элементарные рациональные дроби интегрируемы и интеграл от них представим в виде суммы рациональной же функции, логарифмов и арктангенсов. Что и доказывает теорему. ◄
§ 6. Метод рационализации подынтегрального выражения Интеграл от произвольной функции с помощью свойств и правил интегрирования сводят к рациональной функции. По схеме, изложенной в теореме 5, проводят интегрирование рациональной дроби. Этот прием и называется методом рационализации подынтегрального выражения. Можно рассматривать рациональные функции от двух переменных (вполне аналогично можно рассматривать рациональные функции от трех и более переменных). Определение 5. Рациональной функцией или рациональной дробью R(x,y) от двух переменных (x,y) называют отношение двух алгебраических полиномов
Так же, как и для одной переменной, множество рациональных дробей от двух переменных обладает рядом почти очевидных свойств.
Свойства рациональных дробей
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 706; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.011 с.) |

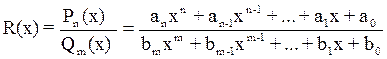 .
.
 .
.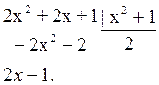
 II.
II.  (k >1) III.
(k >1) III.  IV.
IV.  (m>1).
(m>1). нет вещественных корней, т. е.
нет вещественных корней, т. е.  , в противном случае дробь типа III или IV можно преобразовать путем разложения знаменателя к рациональным дробям типа I или II.
, в противном случае дробь типа III или IV можно преобразовать путем разложения знаменателя к рациональным дробям типа I или II. .
. .
.
 и сделаем подстановку
и сделаем подстановку  ; dx = du. Используя табличный интеграл №6 и правило интегрирования №3, получаем
; dx = du. Используя табличный интеграл №6 и правило интегрирования №3, получаем
 .
.
 .
.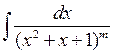 .
. .
. правильная рациональная дробь с вещественными коэффициентами, знаменатель которой имеет вид
правильная рациональная дробь с вещественными коэффициентами, знаменатель которой имеет вид ,
,

 .
. .
.

 .
. .
. .
. .
.


