
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование квадратичных иррациональностейСодержание книги
Поиск на нашем сайте
(Подстановки Эйлера)
Рассмотрим интегрируемость в элементарных функциях любой функции вида Мы докажем, что интеграл от вышеприведенной функции всегда рационализируется одной из так называемых подстановок Эйлера. Сначала рассмотрим случай, когда квадратичный трехчлен ax2 + bx + cимеет комплексные корни. В этом случае знак квадратного трехчлена совпадает со знаком а, и поскольку по смыслу квадратный трехчлен (из которого извлекается квадратный корень) положителен, то а >0. Таким образом, мы имеем право сделать следующую подстановку
Эту подстановку обычно называют первой подстановкой Эйлера. Докажем, что эта подстановка рационализирует интеграл от функции для рассматриваемого случая. Возводя в квадрат обе части равенства
Таким образом, в правой части равенства
мы получаем интеграл от рациональной дроби. Рассмотрим теперь случай, когда квадратный трехчлен и меет несовпадающие вещественные корни x1 и х2. В таком случае ax2 + bx + c = a(x - x1)(x - x2). Докажем, что в этом случае интеграл от функции рационализируется посредством подстановки
называемой обычно третьей подстановкой Эйлера. В самом деле, так как ax2 + bx + c = a(x - x1)(x - x2), то
и, следовательно,
Таким образом, после подстановки все переменные функции R выражаются через рациональные функции от t. В силу третьего свойства рациональных дробей мы снова получаем рациональную дробь от t. Этими двумя подстановками рационализируется любая функция вида Упражнение 11. (Вторая подстановка Эйлера) Рационализировать интеграл
Рассмотрим несколько примеров на Эйлеровы подстановки.
1. К вычислению интеграла можно применить I подстановку, хотя второй основной интеграл
нам уже известен из элементарных соображений, но – для тренировки - мы все же к нему применим эйлеровы подстановки. Если воспользоваться сначала III подстановкой
и
Так как имеет место тождество
то этот результат лишь формой разнится от известного нам. Читателю и впредь следует считаться с возможностью для интеграла получаться в разных формах, в зависимости от примененного для его вычисления метода. Если к тому же интегралу применить II подстановку то аналогично получим
Здесь мы сталкиваемся с другим любопытным обстоятельством, этот результат годится отдельно для промежутка
лишено смысла. Пределы этого выражения при И на этот раз мы получили прежний результат лишь в другой форме, ибо имеют место тождества
2. Сначала применим I подстановку
Если подставить сюда
Применим теперь II подстановку
Остается подставить сюда
Это выражение хотя и разнится от ранее полученного по форме, но при С`=C+3/2 отождествляется с ним. 3. Так как корни подкоренного выражения вещественны, то можно применить III подстановку Имеем
и
куда еще нужно подставить для получения окончательного результата
Воспользовавшись формулой для суммы арктангенсов, а также очевидным соотношением
можно придать результату более простую форму
Если к тому же интегралу применить II подстановку то получим, что
при 4. I подстановка: Имеем
Таким образом, вопрос сводится к вычислению элементарного интеграла; в результате надлежит подставить
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 726; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.93.61 (0.006 с.) |

 , где а, bи с – некоторые постоянные. Функцию такого вида будем называть квадратичной иррациональностью. При этом мы, конечно, считаем, что квадратичный трехчлен ax2+bx+c не имеет равных корней (иначе корень из этого трехчлена может быть заменен рациональным выражением).
, где а, bи с – некоторые постоянные. Функцию такого вида будем называть квадратичной иррациональностью. При этом мы, конечно, считаем, что квадратичный трехчлен ax2+bx+c не имеет равных корней (иначе корень из этого трехчлена может быть заменен рациональным выражением). .
. , получим,
, получим,  ,так что
,так что .
. ,
, ,
,
 .
. , но при c > 0 возможна вторая подстановка Эйлера.
, но при c > 0 возможна вторая подстановка Эйлера.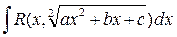 подстановкой
подстановкой  , при условии c >0
, при условии c >0 .
.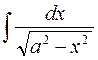
 , то
, то ,
, .
.
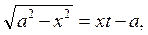
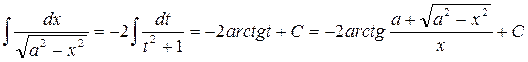 .
. и для промежутка
и для промежутка  , ибо в точке x=0 выражение
, ибо в точке x=0 выражение
 и при
и при  различны: они равны соответственно p и -p; выбирая для упомянутых промежутков различные же значения постоянной C так, чтобы второе из них было на 2p больше первого, можно составить функцию, непрерывную во всем промежутке
различны: они равны соответственно p и -p; выбирая для упомянутых промежутков различные же значения постоянной C так, чтобы второе из них было на 2p больше первого, можно составить функцию, непрерывную во всем промежутке  , если принять за ее значение при x=0 общий предел слева и справа.
, если принять за ее значение при x=0 общий предел слева и справа.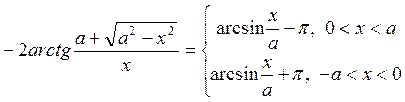 .
. .
.
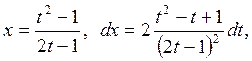

 .
. , то окончательно получим
, то окончательно получим

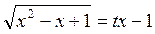 ,
,

 .
. после очевидных упрощений получим
после очевидных упрощений получим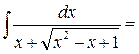


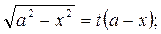 здесь
здесь 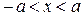 и
и  .
.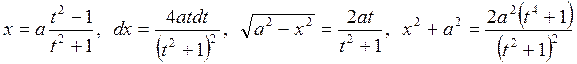 ,
,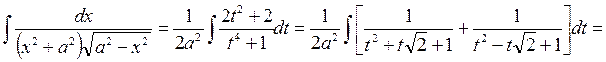
 ,
,
 (при "a),
(при "a), (где
(где  )
)

 Этот результат годится в отдельности для промежутка
Этот результат годится в отдельности для промежутка  и для промежутка
и для промежутка  легко сообразить, что изменяя значения постоянной С` при переходе x через 0, можно сделать его пригодным во всем промежутке
легко сообразить, что изменяя значения постоянной С` при переходе x через 0, можно сделать его пригодным во всем промежутке  . Наконец, если преобразовать его по формуле для суммы арктангенсов, то он отождествится с предыдущим результатом.
. Наконец, если преобразовать его по формуле для суммы арктангенсов, то он отождествится с предыдущим результатом.






