
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции в точке. СвойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Функция непрерывна на интервале, если она непрерывна в любой точке этого интервала Свойства непрерывных функций: 1. Если f1(x) и f2(x) непрерывны в точке а, то непрерывна их сумма, произведение и частное. 2. Если функция u=fi(x) непрерывна в точке а, а функция y=f(u) непрерывна в точке u0=fi(a), то непрерывна сложная функция y=f(fi(x)) в х=а 3. Если непрерывная функция имеет однозначную обратную функцию, то эта обратная функция непрерывна. 4. Все основные элементарные функции непрерывны там, где они определены. Т.е. во всех точ Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е. Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва. Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию верно неравенство Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной. f(x) = f(x0) + (x) где (х) – бесконечно малая при хх0. Свойства непрерывных функций. 1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0. 2) Частное двух непрерывных функций
Точки разрыва, их классификация Точка а называется точкой разрыва функции, если эта функция в точке а не является непрерывной. Точка а называется точкой разрыва первого рода, если существуют конечные односторонние пределы и они не равны друг другу. Точка а назывется точкой разрыва второго рода, если в этой точке функция не имеет хотя бы одного одностороннего предела или хотя бы 1 односторонний предел равен бесконечности или минус бесконечности. Точка а называется устранимой, если существуют конечные односторонние пределы и они равны друг другу, но не равны значению функции в этой точке.
Производная функции, ее геометрический и механический смысл Производной от функции
Геометрически производная представляет собой угловой коэффициент касательной к графику функции Производная есть скорость изменения функции в точке х. Отыскание производной называется дифференцированием функции.
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

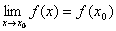
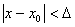
 .
.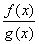 – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0. называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю: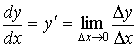 , или
, или  .
.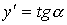 .
.


