

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Экстремум функции, необходимое и достаточные условия экстремума
ЭКСТРЕМУМ ФУНКЦИИ [extremum] — термин, объединяющий понятия максимума и минимума функции.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами
Теорема.(Необходимое условие экстремума). Если функция y =f(x) в точке х0 имеет экстремум, то производная f/(x 0 ) равна нулю
Теорема(Достаточное условие экстремума).
Пусть функция f(x) непрерывна на отрезке [a, b], а точка x0 из этого отрезка является критической. Тогда:
1) если f/(x) < 0 на (a;x0) и f/(x) > 0 на (x0;b), то точка x0–точка минимума функции f(x);
2) если f/(x) > 0 на (a;x0) и f/(x) < 0 на (x0;b), то точка x0–точка максимума функции f(x).
2 Решение систем линейных алгебраических уравнений методом Гаусса, по правилу Крамера, с помощью обратной матрицы
Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Если det A ≠ 0, то существует обратная матрица  . Тогда решение СЛАУ записывается в виде: . Тогда решение СЛАУ записывается в виде:  . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
3 Векторы, основные определения, понятия, действия над ними.
Вектор – это направленный отрезок прямой.
Нулевой вектор . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
3 Векторы, основные определения, понятия, действия над ними.
Вектор – это направленный отрезок прямой.
Нулевой вектор  – это любая точка плоскости или пространства.
Длина вектора – это любая точка плоскости или пространства.
Длина вектора  - это неотрицательное число, равное длине отрезка АВ.
Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.
Два коллинеарных вектора - это неотрицательное число, равное длине отрезка АВ.
Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.
Два коллинеарных вектора  и и  называют сонаправленными, если их направления совпадают и обозначают называют сонаправленными, если их направления совпадают и обозначают  .
Два вектора называются равными, если они сонаправленные и их длины равны.
Два вектора называются противоположными, если они противоположно направлены и их длины равны.
Угол .
Два вектора называются равными, если они сонаправленные и их длины равны.
Два вектора называются противоположными, если они противоположно направлены и их длины равны.
Угол  называется углом между векторами называется углом между векторами  и и  .
Два вектора называются перпендикулярными, если угол между ними равен 90градусам (или .
Два вектора называются перпендикулярными, если угол между ними равен 90градусам (или  радиан).
4 Линейные операции над векторами, заданными в координатной форме
Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число. 1) Сумма радиан).
4 Линейные операции над векторами, заданными в координатной форме
Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число. 1) Сумма 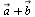 векторов векторов  и и  находится по правилу треугольника или по правилу параллелограмма
— эти правила равносильны. Сложение векторов коммутативно и ассоциативно: находится по правилу треугольника или по правилу параллелограмма
— эти правила равносильны. Сложение векторов коммутативно и ассоциативно:   Разность векторов Разность векторов  можно определить как сумму можно определить как сумму  , т. е. вычитание заменяется прибавлением противоположного вектора. 2) Произведением , т. е. вычитание заменяется прибавлением противоположного вектора. 2) Произведением 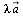 (или (или  ) вектора ) вектора  на действительное число λ называется вектор на действительное число λ называется вектор  , коллинеарный вектору , коллинеарный вектору  , имеющий длину, равную , имеющий длину, равную 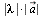 , и то же направление, что и вектор , и то же направление, что и вектор  , если λ > 0, и направление, противоположное направлению вектора , если λ > 0, и направление, противоположное направлению вектора  , если λ < 0
.
5 Коллинеарность и компланарность векторов
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.
Условия коллинеарности векторов , если λ < 0
.
5 Коллинеарность и компланарность векторов
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.
Условия коллинеарности векторов
- Два вектора коллинеарные, если отношения их координат равны.
- Два вектора коллинеарные, если их векторное произведение равно нулю.
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.
Условия компланарности векторов
- Три вектора компланарны если их смешанное произведение равно нулю.
- Три вектора компланарны если они линейно зависимы.
6 Скалярное, векторное, смешанное произведения векторов, определения, свойства, геометрический смысл векторного и смешанного произведений.
Определение:Под скалярным произведением двух векторов  и и  понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.  = =   , ,  - угол между векторами - угол между векторами  и и  .
Определение: Под векторным произведением двух векторов .
Определение: Под векторным произведением двух векторов 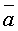 и и  понимается вектор, понимается вектор,  для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е. для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е.  , где , где  угол между векторами угол между векторами 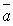 и и  -этот вектор перпендикулярен перемножаемым векторам,
7 Уравнения прямой на плоскости: с угловым коэффициентом; через две точки; в отрезках, общее уравнение
Уравнение прямой на плоскости - определение.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и в ней задана прямая линия.
Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости.
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.
Уравнение прямой с угловым коэффициентом имеет вид
-этот вектор перпендикулярен перемножаемым векторам,
7 Уравнения прямой на плоскости: с угловым коэффициентом; через две точки; в отрезках, общее уравнение
Уравнение прямой на плоскости - определение.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и в ней задана прямая линия.
Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости.
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.
Уравнение прямой с угловым коэффициентом имеет вид  , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки: , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
 Определение.Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
8 Уравнение плоскости в векторной и координатной формах.
Общее уравнение плоскости в системе координат записывается следующим образом:
Определение.Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
8 Уравнение плоскости в векторной и координатной формах.
Общее уравнение плоскости в системе координат записывается следующим образом:
|
|



 . Тогда решение СЛАУ записывается в виде:
. Тогда решение СЛАУ записывается в виде:  . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
3 Векторы, основные определения, понятия, действия над ними.
Вектор – это направленный отрезок прямой.
Нулевой вектор
. Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
3 Векторы, основные определения, понятия, действия над ними.
Вектор – это направленный отрезок прямой.
Нулевой вектор  – это любая точка плоскости или пространства.
Длина вектора
– это любая точка плоскости или пространства.
Длина вектора  - это неотрицательное число, равное длине отрезка АВ.
Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.
Два коллинеарных вектора
- это неотрицательное число, равное длине отрезка АВ.
Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.
Два коллинеарных вектора  и
и  называют сонаправленными, если их направления совпадают и обозначают
называют сонаправленными, если их направления совпадают и обозначают  .
Два вектора называются равными, если они сонаправленные и их длины равны.
Два вектора называются противоположными, если они противоположно направлены и их длины равны.
Угол
.
Два вектора называются равными, если они сонаправленные и их длины равны.
Два вектора называются противоположными, если они противоположно направлены и их длины равны.
Угол  называется углом между векторами
называется углом между векторами  и
и  .
Два вектора называются перпендикулярными, если угол между ними равен 90градусам (или
.
Два вектора называются перпендикулярными, если угол между ними равен 90градусам (или  радиан).
4 Линейные операции над векторами, заданными в координатной форме
Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число. 1) Сумма
радиан).
4 Линейные операции над векторами, заданными в координатной форме
Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число. 1) Сумма 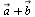 векторов
векторов  и
и  находится по правилу треугольника или по правилу параллелограмма
— эти правила равносильны. Сложение векторов коммутативно и ассоциативно:
находится по правилу треугольника или по правилу параллелограмма
— эти правила равносильны. Сложение векторов коммутативно и ассоциативно: 
 Разность векторов
Разность векторов  можно определить как сумму
можно определить как сумму  , т. е. вычитание заменяется прибавлением противоположного вектора. 2) Произведением
, т. е. вычитание заменяется прибавлением противоположного вектора. 2) Произведением 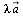 (или
(или  ) вектора
) вектора 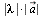 , и то же направление, что и вектор
, и то же направление, что и вектор  и
и  понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.  =
= 
 ,
,  и
и 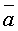 и
и  понимается вектор,
понимается вектор,  для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е.
для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е.  , где
, где  угол между векторами
угол между векторами 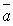 и
и  -этот вектор перпендикулярен перемножаемым векторам,
7 Уравнения прямой на плоскости: с угловым коэффициентом; через две точки; в отрезках, общее уравнение
Уравнение прямой на плоскости - определение.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и в ней задана прямая линия.
Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости.
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.
Уравнение прямой с угловым коэффициентом имеет вид
-этот вектор перпендикулярен перемножаемым векторам,
7 Уравнения прямой на плоскости: с угловым коэффициентом; через две точки; в отрезках, общее уравнение
Уравнение прямой на плоскости - определение.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и в ней задана прямая линия.
Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости.
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.
Уравнение прямой с угловым коэффициентом имеет вид  , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
, где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
 Определение.Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
8 Уравнение плоскости в векторной и координатной формах.
Общее уравнение плоскости в системе координат записывается следующим образом:
Определение.Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
8 Уравнение плоскости в векторной и координатной формах.
Общее уравнение плоскости в системе координат записывается следующим образом:



