Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители второго и третьего порядка, их свойства, вычисление разложениемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определители второго и третьего порядка, их свойства, вычисление разложением по элементам строки (столбца), по правилу треугольника Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом: Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом: Определитель не изменяется при транспонировании, т.е. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е. Определитель, имеющий нулевую строку, равен 0. Определитель, имеющий две равные строки, равен 0. Определитель, две строки которого пропорциональны, равен 0. При перестановке двух строк определителя он умножается на –1. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число. Разложение определителя по строке. Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент. Алгебраическим дополнением элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е. Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е. где i=1,2,3.
на число, сложение и умножение матриц. Первый замечательный предел Первым замечательным пределом называется предел
Первый замечательный предел равен
Второй замечательный предел Вторым замечательным пределом называется предел
Число Теорема 2.15 Второй замечательный предел существует. Его значение
Раскрытие неопределенностей Неопределенности типа Пусть заданы две функции f (x) и g (x), такие, что
В этом случае говорят, что функция Неопределенности типа Пусть две функции f (x) и g (x) обладают свойством
где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция
Правила дифференцирования Правило Лопиталя Теорема 5.5 (Правило Лопиталя) Пусть функции
Признак убывания функции Если f’(x)<0 на некотором промежутке, то функция f(x) убывает на данном промежутке. Строгое доказательство этих двух признаков изучается в курсе математического анализа, здесь же мы его приводить не будем. Определение: x0 называется критической точкой функции f(x), если 1) x0 – внутренняя точка области определения f(x); 2) f'(x0)=0 или f'(x0) не существует.
Теоремы Ферма, Ролля Теорема Ферма. (Ферма, 1601-1665 – французский математик). Пусть функция f(x), определенная в интервале (a, b), принимает в некоторой точке x=c этого интервала наибольшее или наименьшее значение. В таком случае, если в точке x=c существует производная этой функции, то она равна нулю. Теорема Ролля (Ролль, 1652-1719 – французский математик). Если функция f(x) непрерывна на сегменте [a, b], дифференцируема во всех его внутренних точках и на концах сегмента обращается в нуль, то есть f(a)=f(b)=0, то ее производнаяf/(x) обращается в нуль хотя бы в одной внутренней точке x=c этого сегмента. Теорема 1. Если переменная величина принимает только неотрицательные значения (y=f(x)0), то ее предел (если он существует) не может быть числом отрицательным. Теорема 2. Если переменная величина принимает только неположительные значения (y=f(x)0), то ее предел (если он существует) не может быть числом положительным. Теорема 3. Если переменная величина имеет предел, отличный от нуля, то начиная с некоторого момента, она принимает значения только того знака, каков знак ее предела.
Теоремы Лагранжа, Коши Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [ а; b ]; 2) дифференцируемы в интервале (а; b); 3) g' (x) ≠ 0 в этом интервале, то в интервале (а; b) существует такая точка с, что имеет место равенство
Окружность Парабола
Определители второго и третьего порядка, их свойства, вычисление разложением по элементам строки (столбца), по правилу треугольника Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом: Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом: Определитель не изменяется при транспонировании, т.е. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е. Определитель, имеющий нулевую строку, равен 0. Определитель, имеющий две равные строки, равен 0. Определитель, две строки которого пропорциональны, равен 0. При перестановке двух строк определителя он умножается на –1. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
|
|||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1010; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 называется прямоугольная таблица, содержащая
называется прямоугольная таблица, содержащая  чисел, состоящая из
чисел, состоящая из  строк и
строк и  столбцов.
Основными арифметическими операциями над матрицами являются умножение матрицы
столбцов.
Основными арифметическими операциями над матрицами являются умножение матрицы
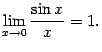


 , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число
, заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число  и
и  .
.

 имеет неопределенность типа
имеет неопределенность типа 

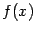 и
и  непрерывны в некоторой окрестности
непрерывны в некоторой окрестности  точки
точки  и
и  , то есть
, то есть  и
и  при
при  . Предположим, что при
. Предположим, что при  функции
функции  и
и  , причём существует предел отношения этих производных:
, причём существует предел отношения этих производных: