
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства определителей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вопрос 1 Ответ: Матрицей называется прямоугольная таблица чисел. Обозначения: А – матрица,
Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы. Квадратная матрица называется треугольной, если ее элементы, стоящие выше (ниже) главной диагонали, равны нулю. Диагональная матрица — квадратная матрица, у которой все внедиагональные элементы равны нулю. Скалярная матрица —диагональная матрица, элементы главной диагонали которой равны. Частным случаем скалярной матрицы является единичная матрица - матрица, все диагональные элементы которой единицы, а остальные - нули: Единичная матрица чаще всего обозначается буквой E или En, где n - порядок матрицы. Линейные операции над матрицами 1. Сложение матриц. Суммой матриц А и В одинаковой размерности m Свойства сложения: 1. А + В = В + А. 2. (А + В) + С = А + (В + С). 3. Если О – нулевая матрица, то А + О = О + А = А Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц. Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности. Пример.
2. Умножение матрицы на число. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число. Свойства умножения матрицы на число: 1. (km)A=k(mA). 2. k(A + B) = kA + kB. 3. (k + m)A = kA + mA. Замечание 1. Справедливость свойств следует из определений сложения и умножения Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е. С = А + (-1)В.
Пример.
Перемножение матриц. Выше было указано, что сложение матриц накладывает условия на размерности слагаемых. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго. Произведением матрицы А размерности m Пример.
Найдем элементы матрицы С:
Итак, Теорема 3.1 (без доказательства). Определитель произведения двух квадратных матриц равен произведению их определителей. Замечание. Операция перемножения матриц некоммутативна, т.е. Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны. Однако в некоторых случаях произведения АВ и ВА совпадают. Рассмотрим произведение квадратной матрицы А на единичную матрицу Е того же порядка:
Тот же результат получим и для произведения ЕА. Итак, для любой квадратной матрицы А АЕ = ЕА =А.
Вопрос 2 Ответ: Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
Квадратная матрица называется вырожденной, если её определитель равен нулю. Квадратная матрица называется невырожденной, если её определитель отличен от нуля. Определитель произведения квадратных матриц равен произведению определителейсомножителей. Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.Обозначение: Пример. Для Алгебраическим дополнением
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.Примеры. 1. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:
Примеры.1. 2.
Вопрос 4. Ответ: Линейным уравнением называется уравнение вида Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число. Системой линейных уравнений (линейной системой) называется система вида
Решением линейной системы называется набор чисел Решение системы линейных уравнений матричным методом Еще один, пользующийся большой популярностью метод. Этот способ или, как его еще называют, метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу. Для того, что бы расставить все точки над и, рассмотрим метод под микроскопом. Алгоритм решения достаточно просто. Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A-1, получим A-1AX= A-1B, откуда EX=X=A-1B. Следовательно, матрица-решение X легко находится как произведение A-1 и B.Для большей ясности решим небольшой пример методом обратной матрицы: 21x1-45x2-3.5x3=10 12x1-16x2+21x3=-16 14x1+13x2-8x3=10 Определим совместность системы уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, чтобы ранг основной матрицы
и ранг расширенной матрицы
были равны.Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.Для решения методом обратной матрицы необходимо ввести матричные обозначения
Найдем обратную матрицу A-1. Как ее найти, показывать не будем. Воспользовавшись нашии онлайн калькулятором, вы сможете выбрать один из двух способов для ее нахождения. Она будет иметь вид.
Для нахождения матрицы X умножим обратную матрицу А-1 на матрицу С
Получили решение системы уравнений Правило Крамера. Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель
Предположим сначала, что Сложив затем все уравнения, получим:
Отметим, что (j-й столбец) (Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при Предположим теперь, что В этом случае, если все Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии: 2) Если 3) Если 4) Если
Вопрос 5 1) Минор n-ого порядка.
2) Ранг матрицы. Ответ 1. Рангом матрицы Единое, стандартное, обозначение ранга матрицы отсутствует. Однако ув. Глухов показывал нам, что он обозначается как rang A (основной) и rang A (“A” с черточкой наверху – расширенный ранг), позже покажу. 2. Теперь то, что касается ранга матрицы.
Теперь возвращаемся к рангам. Вспоминаем, что ранг – это НАИБОЛЬШИЙ из порядков МИНОРОВ. Всего таких порядков может быть дохуища, все зависит от того, насколько огромна матрица. В данной матрице порядков будет не более 3, но еще неизвестно, сколько из них будут не равны нулю. Начинаем по порядку. Ищем миноры ПЕРВОГО порядка. Таковым является любое число в матрице.
Таким образом 1,4,5 у меня миноры ПЕРВОГО порядка. Ищем миноры ВТОРОГО порядка. Это будет пересечение строк и столбцов (т.е. то, что мы рассматривали выше). Найдем минор 3 строки 3 столбца.
Дальше рассматриваем минор третьего порядка. Это определитель который мы считали треугольниками.
Видим, что максимальный порядок, т.е. ТРЕТИЙ - НЕ РАВЕН (если бы 3ий порядок был равен нулю, было бы rang=2) нулю, следовательно ранг матрицы = 3 (rang A = 3) Думаю, с этим понятно. Ну это трудный способом, но эффективный, можно посчитать так. Запоминаем, что РАНГ матрицы соответствует НАИБОЛЬШЕМУ порядку не равному нулю. Т.е. если бы у нас определитель третьего порядка был бы =0, то у нас было бы rang A= 2 Есть еще одна фишка. Можно привести матрицу вида
К треугольной, получим
Видно, что число НЕНУЛЕВЫХ строк, равно 3 => rang = 3 это основной ранг матрицы. Но есть и РАСШИРЕННЫЙ. Например, если бы у нас была бы матрица:
То расширенным рангом называлась бы область, которая включает все нули (т.е. 4 столбец), но тем не менее видим, что НУЛЕВЫХ строк нет, следовательно ОСНОВНОЙ ранг равен 3 и ранг РАСШИРЕННЫЙ равен 3 Ну понятно, что если 82.799 было бы равно нулю, то ранг был бы соответственно равен 2. С рангами все, дальше. 3) Теорема Кронекера–Капелли (критерий совместности системы линейных уравнений). Ответ Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы, т.е. Замечание. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений. (об этом позже, это неопределенности) Начнем с охуительного примера. Пример 13. Исследовать систему линейных уравнений Решение. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.
Далее умножим вторую строку на -2 и сложим с третьей, а затем сложим третью строку с последней. Имеем
Вспомнили как решается матрица методом гаусса? Идем дальше. Нас интересует это:
Выше я объяснял, что такое ранг ОСНОВНОЙ и ранг РАСШИРЕННЫЙ. Так вот, согласно теореме Кронекера-Капелли, данная будет несовместной, так как rang A (основной) = 3 (т.к. кол-во НЕНУЛЕВЫХ строк равно 3), а rang A (с черточкой над А, расширенный) = 4. Доказывается эта теорема на примере обычной матрицы, думаю ни у кого не составит труда накалякать матрицу и объяснить. Для танкистов, которые еще не поняли ОСНОВНОЙ и РАСШИРЕННЫЙ ранги: 4) Определенность-неопределенность Ответ Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая. Условие совместности системы линейных уравнений даёт следующая теорема Вопрос 6 1. Вектор. Понятия Ответ: 1) Два вектора коллинеарны, если их отношения равны 2) Два вектора коллинеарны, если их векторное пр-е равно нулю. Пример внизу.
4. Свойства линейных операций над векторами Сложение векторов коммутативно: Сложение векторов ассоциативно: Прибавление нулевого вектора к любому не меняет последнего: Для любого вектора Умножение вектора на число ассоциативно: Дистрибутивность умножения векторов относительно сложения Умножение вектора на число дистрибутивно относительно сложения векторов: Очевидно, умножение на единицу не меняет вектор:
Вопрос 7 1. Базис и система координат на плоскости и в пр-ве Ответ: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов Также говорят, что вектор 1.1 Система координат на плоскости Ответ: Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и размерность по осям. Прямоугольную систему координат вполне можно определить через ортонормированный базис Точка Думаю, всем понятно, что с помощью точки
1.2. Система координат в пр-ве Ответ: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов Напоминаю, также можно сказать, что вектор Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов: Точка
Точка
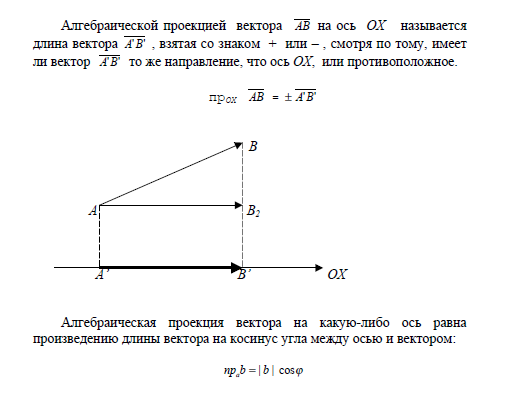
2. Геометрические и алгебраические проекции вектора на ось
3. Координаты вектора на плоскости и в пространстве Начну с векторов на плоскости. Изображаем декартову с.к. и откладываем единичные вектора.
Векторы Ответ: Любой вектор Координаты на плоскости. Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же, только добавится ещё одна координата.
Это есть ортонормированный базис
Вопрос 8 1. Направляющие косинусы вектора Ответ: это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. Следовательно вывод: направление вектора в пространстве определяется углами, которые вектор образует с осями Косинусы этих углов называются направляющими косинусами вектора:
А находят их так: Далее, это орт, он же единичный вектор который находится ТОЧНО так же, как и направляющие косинусы, разве что вместо cos пишем v с галочкой наверху. 2. Сумму векторов и произведение вектора на число находили выше,
Вопрос 9 Ответ: 1. Нахождение координат вектора, зная начало и конец + координаты середины:
2. Расстояние между двумя точками:
Очень простой вопрос, но тем не менее:
Вопрос 10
Вопрос 11 Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).
Векторным произведением вектора а на вектор b называется вектор с, который: 1. Перпендикулярен векторам a и b, т. е. с^а и с^b;
3.Векторы a, b и с образуют правую тройку.
Вопрос 12
Вопрос 13 Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо: 1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём: x + y = y + x − сложение коммутативно; x + (y + z) = (x + y) + z − сложение ассоциативно; x + 0 = x − существует единственный нулевой элемент 0 (x + 0 = x для любого x из L); x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x (x + (−x) = 0 для любого x из L). 2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α· x, наываемый произведением α и x, причём: α·(β · x) = (α·β) · x − умножнение на число ассоциативно:; 1 · x = x − для любого элемента x из L. 3. Операции сложения и умножения на число связаны соотношениями: α·(x + y) = α· x + α· y − умножнение на число дистрибутивно относительно сложения элементов; (α + β )· x = α· x + β · x − умножнение на вектор дистрибутивно относительно сложения чисел. Набор векторов Система из
Система из Замечания 1.2 1. Один вектор 2. Любая часть системы векторов называется подсистемой. Вопрос 14 Прямая на плоскости: Общее уравнение Ax + By + C ( Вектор В векторном виде: Частные случаи: 1) By + C = 0 - прямая параллельна оси Ox; 2) Ax + C = 0 - прямая параллельна оси Oy; 3) Ax + By = 0 - прямая проходит через начало координат; 4) y = 0 - ось Ox; 5) x = 0 - ось Oy.
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Направляющий вектор произвольной прямой в дальнейшем обозначается буквой
Если известна одна точка
Каноническое уравнение прямой
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора Вектор Итак, пусть прямая l проходит через точку М 1(x 1, y 1, z 1), лежащую на прямой параллельно вектору Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что Векторы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 - элемент матрицы,
- элемент матрицы, 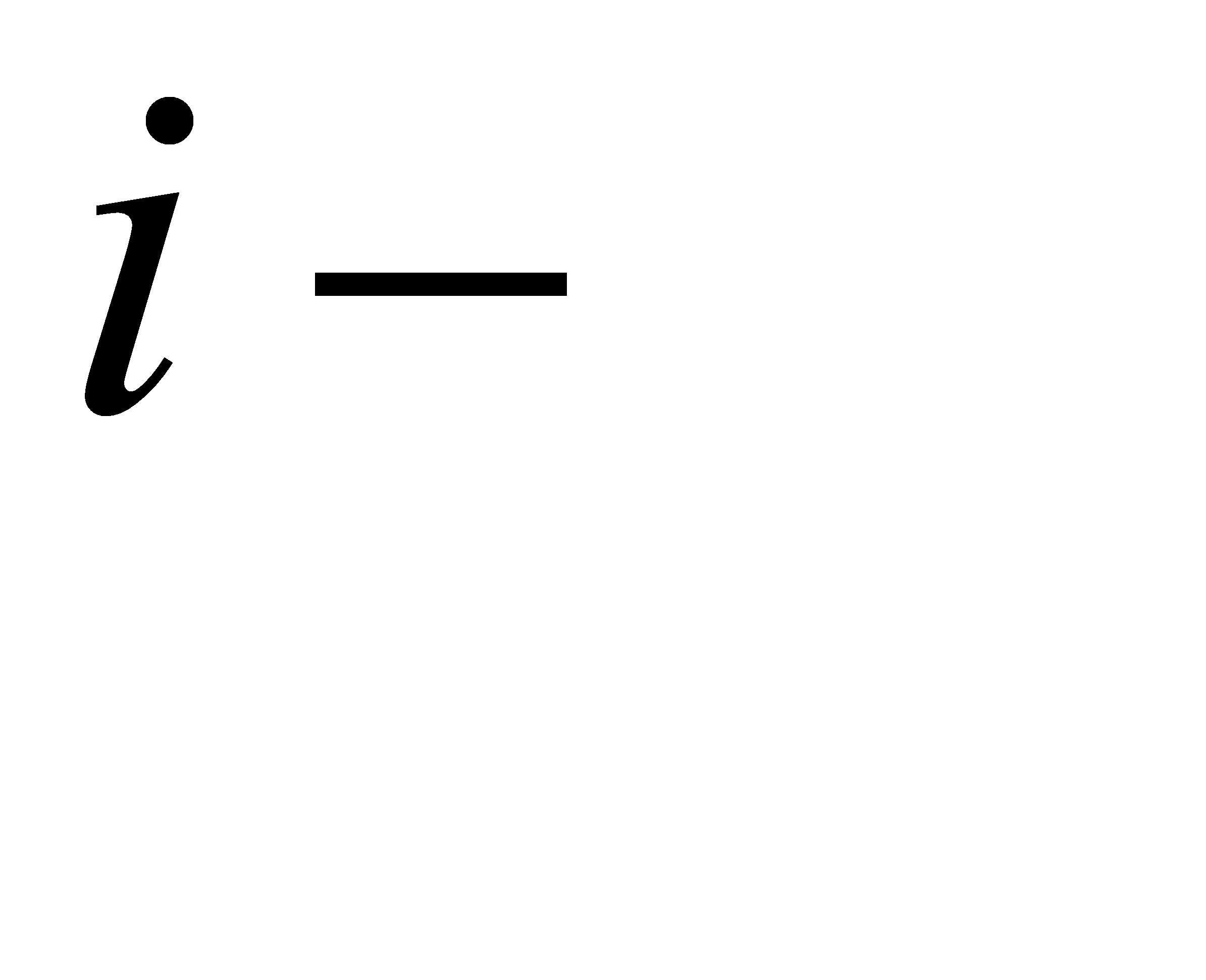 номер строки, в которой стоит данный элемент,
номер строки, в которой стоит данный элемент,  номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов. n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:
n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: 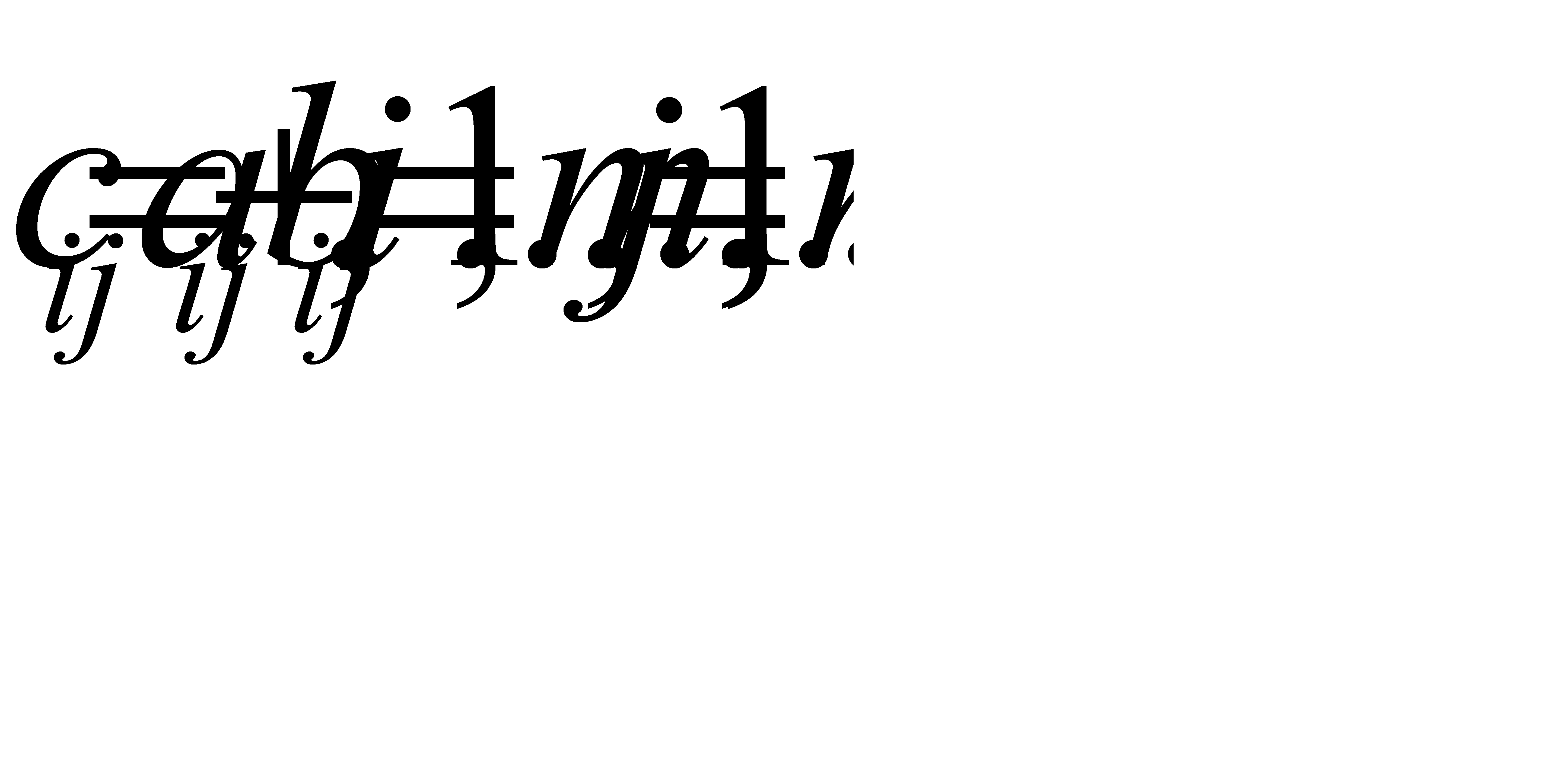
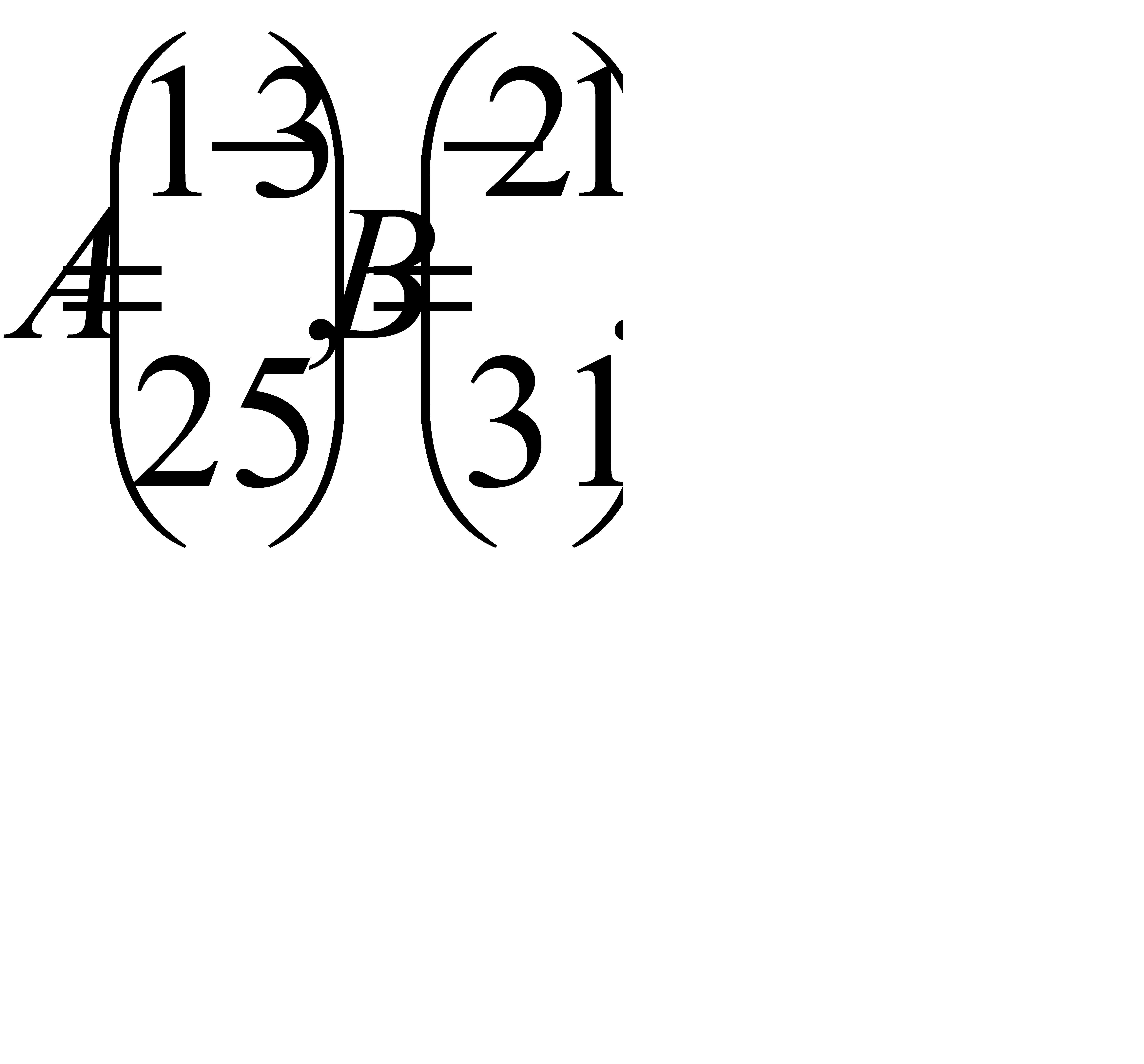

 . Тогда
. Тогда 
 называется матрица С размерности
называется матрица С размерности 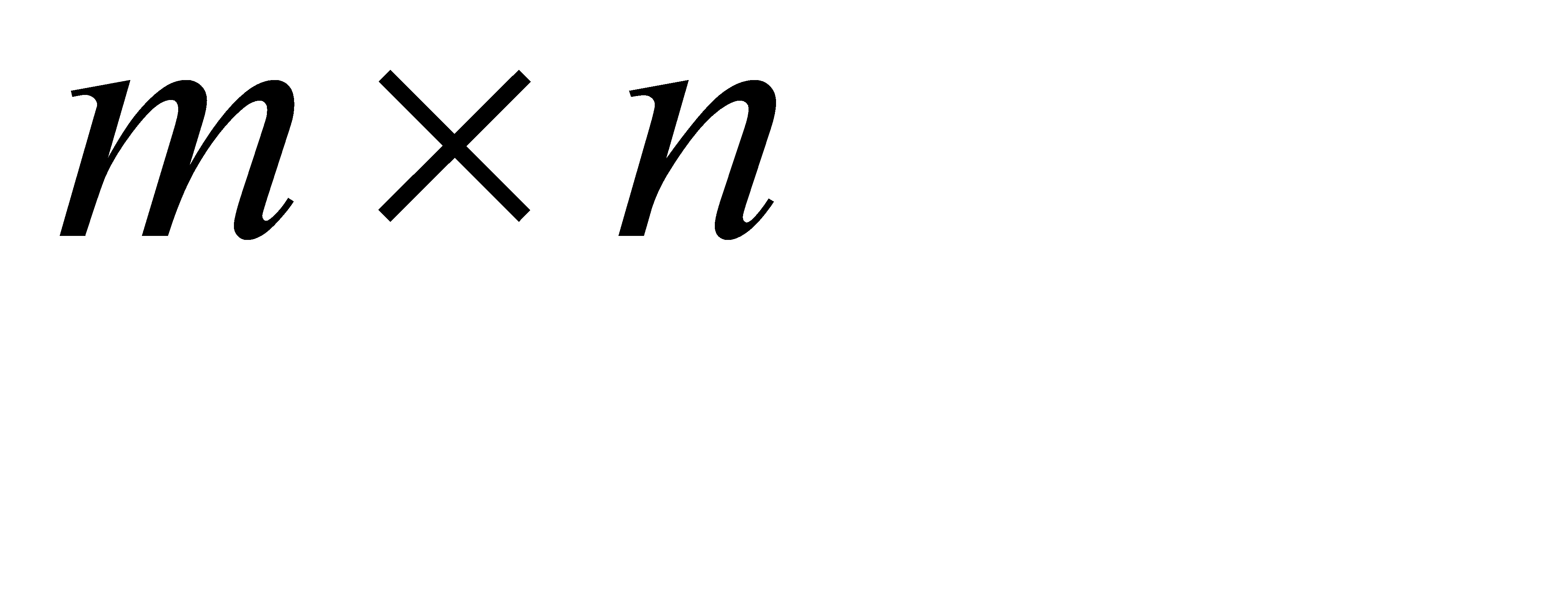 , каждый элемент которой
, каждый элемент которой  определяется формулой:
определяется формулой:  Таким образом, элемент
Таким образом, элемент  . При этом существует произведение АВ, но не существует произведение ВА. Размерность матрицы С=АВ составляет
. При этом существует произведение АВ, но не существует произведение ВА. Размерность матрицы С=АВ составляет 



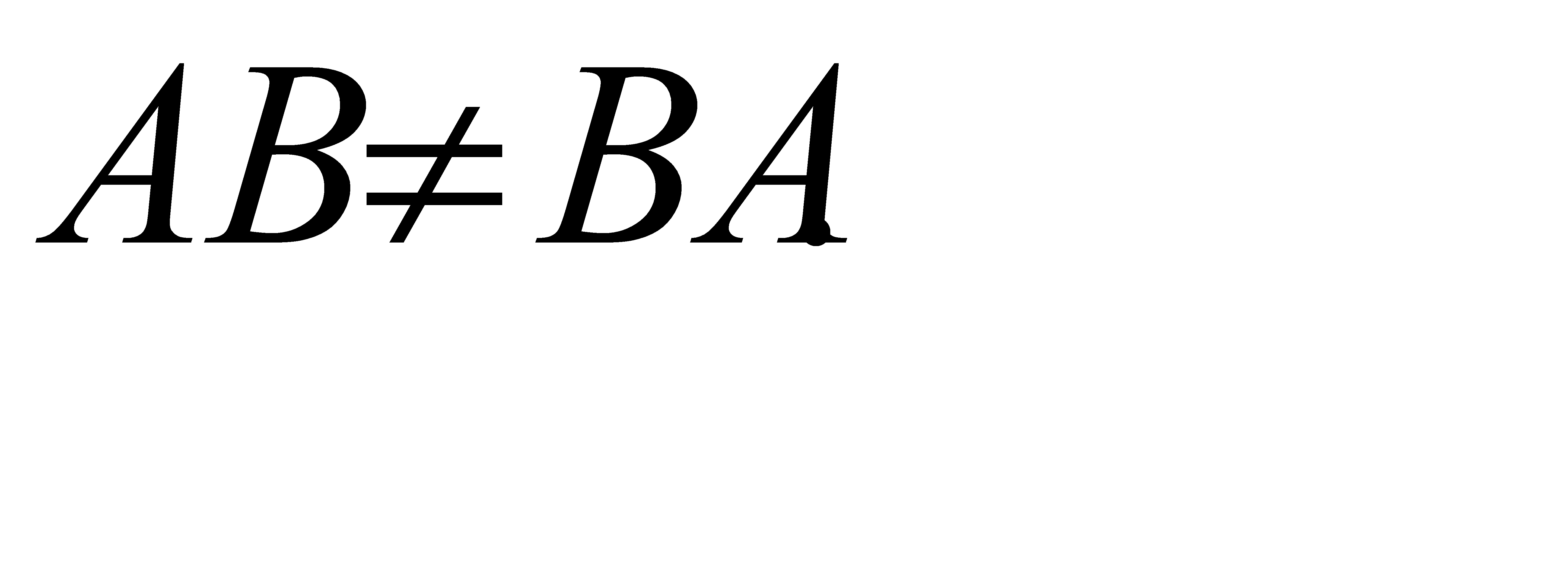 Действительно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей (см. предыдущий пример). Если существуют и АВ, и ВА, то они могут иметь разные размерности (если
Действительно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей (см. предыдущий пример). Если существуют и АВ, и ВА, то они могут иметь разные размерности (если 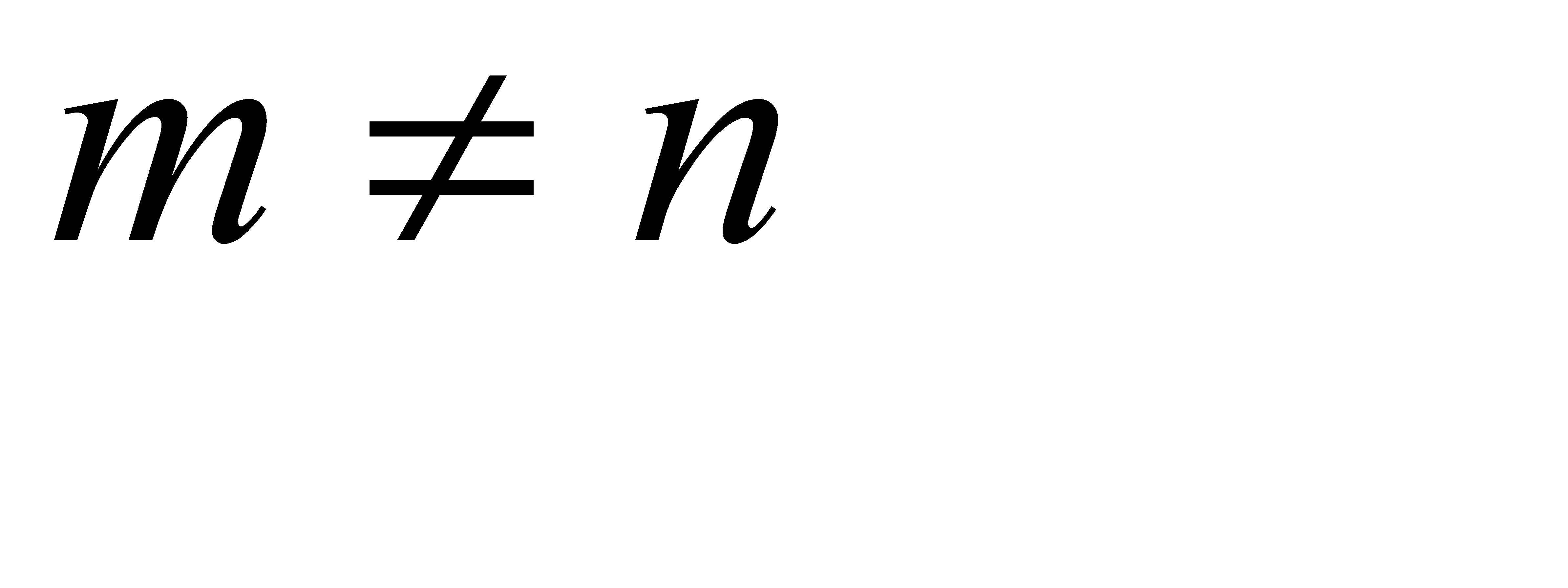 ).
).

 выбранный элемент определителя,
выбранный элемент определителя,  его минор.
его минор.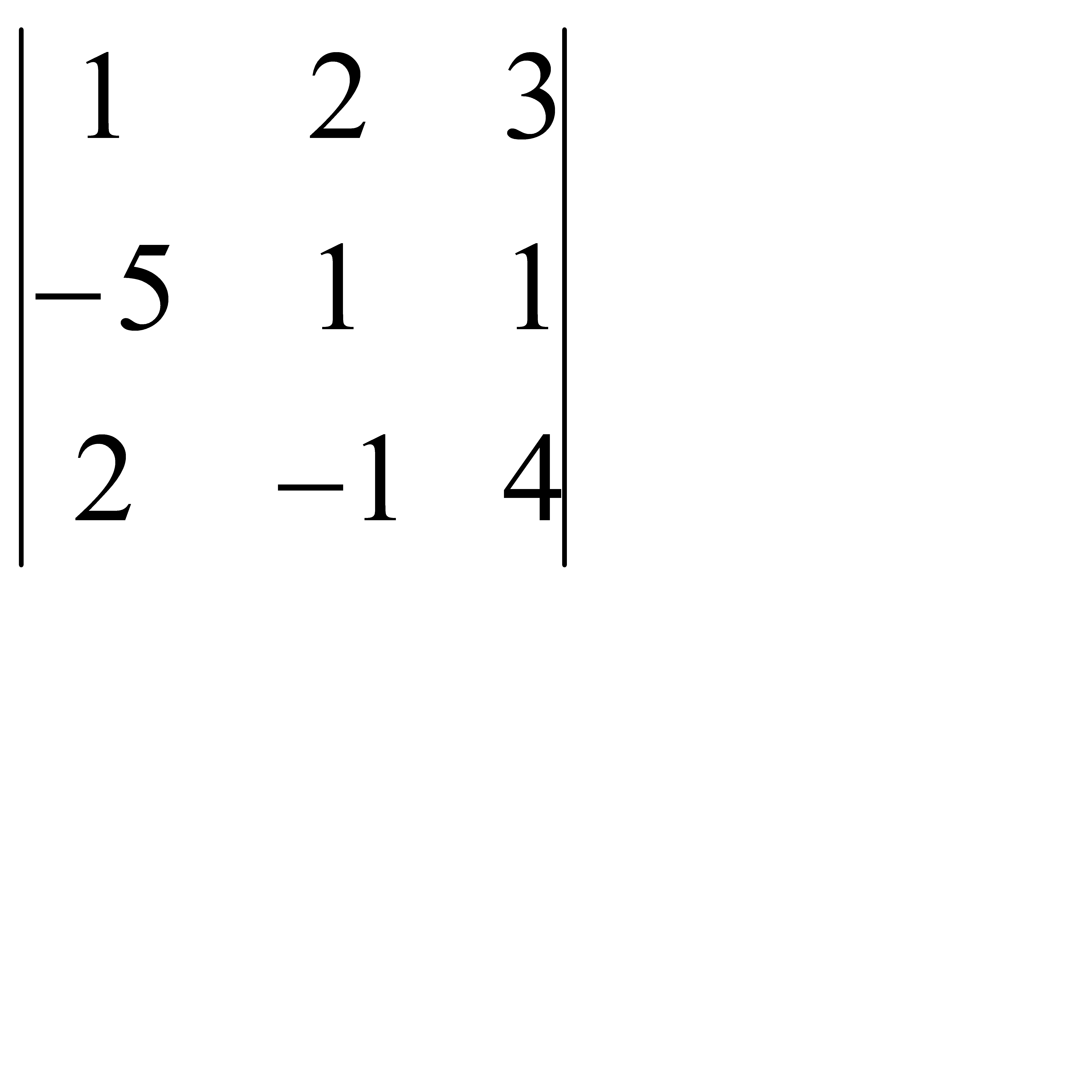

 элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.
элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.  Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом: .
. 2.
2. 

 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 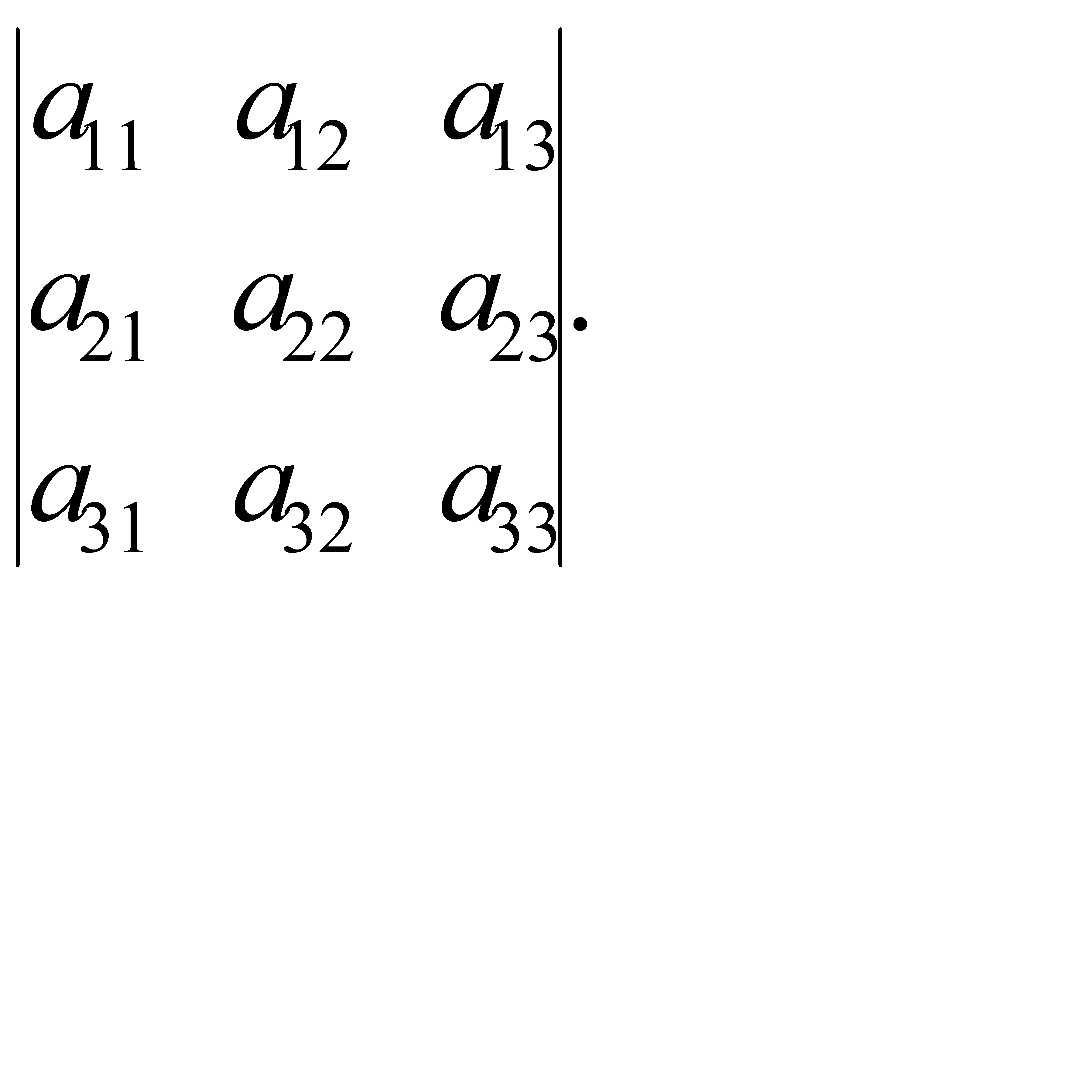


 где
где  и b – числа,
и b – числа,  - неизвестные.
- неизвестные. где
где  - числа,
- числа, 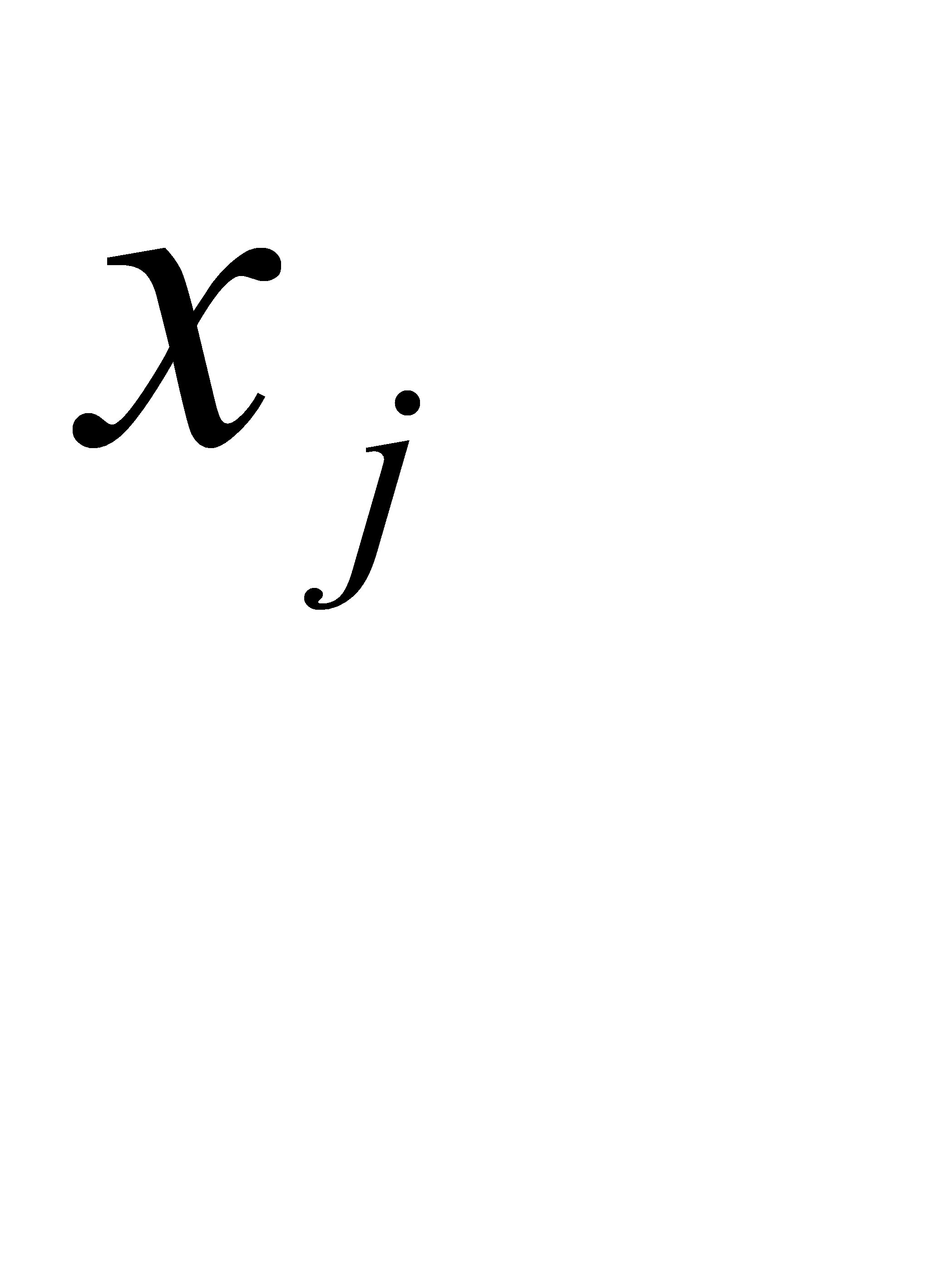 - неизвестные, n – число неизвестных, m – число уравнений.
- неизвестные, n – число неизвестных, m – число уравнений.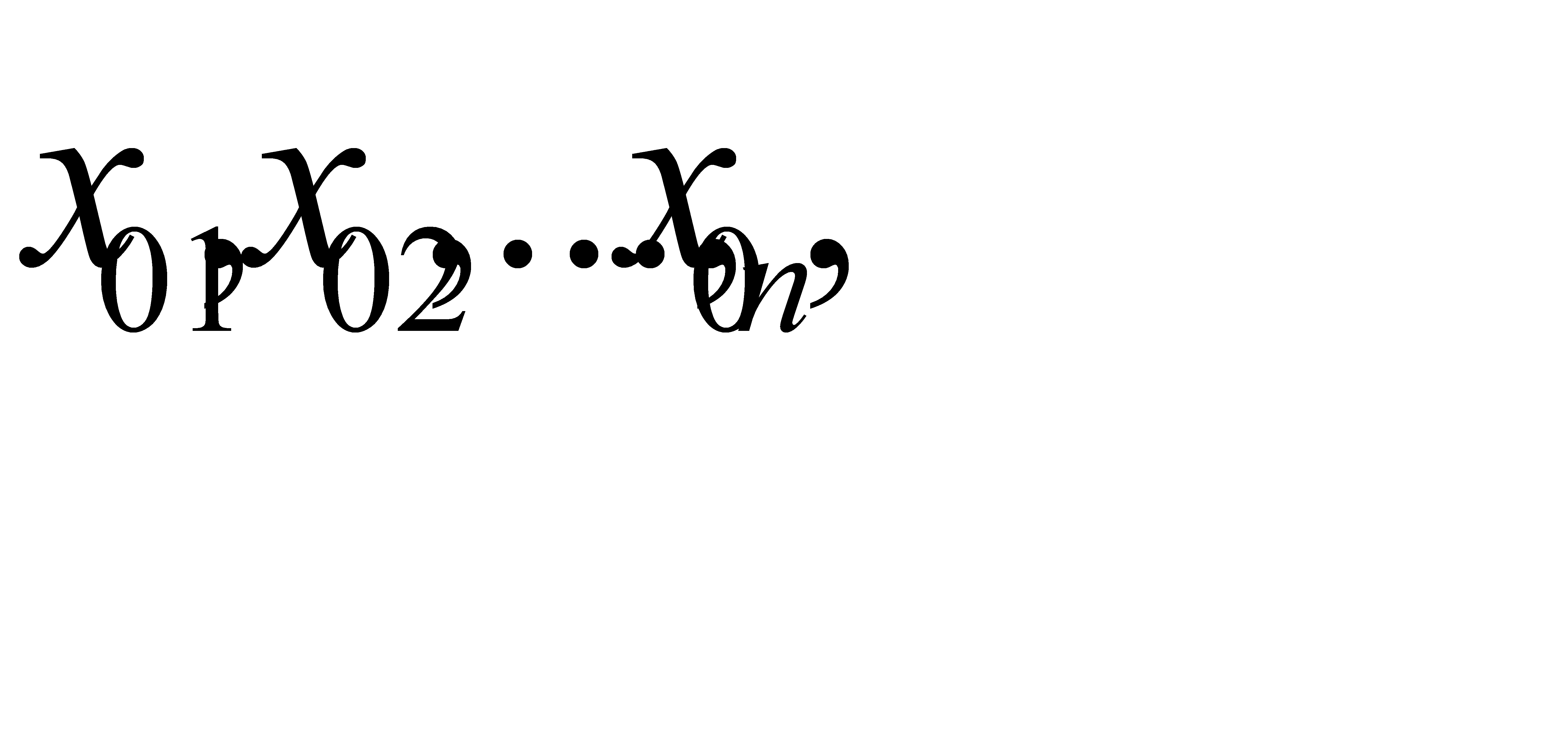 которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство. , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных:
 .
. Умножим каждое уравнение системы (2.3) на алгебраические дополнения
Умножим каждое уравнение системы (2.3) на алгебраические дополнения  элементов j-го столбца
элементов j-го столбца 
 . (2.5)
. (2.5) .
.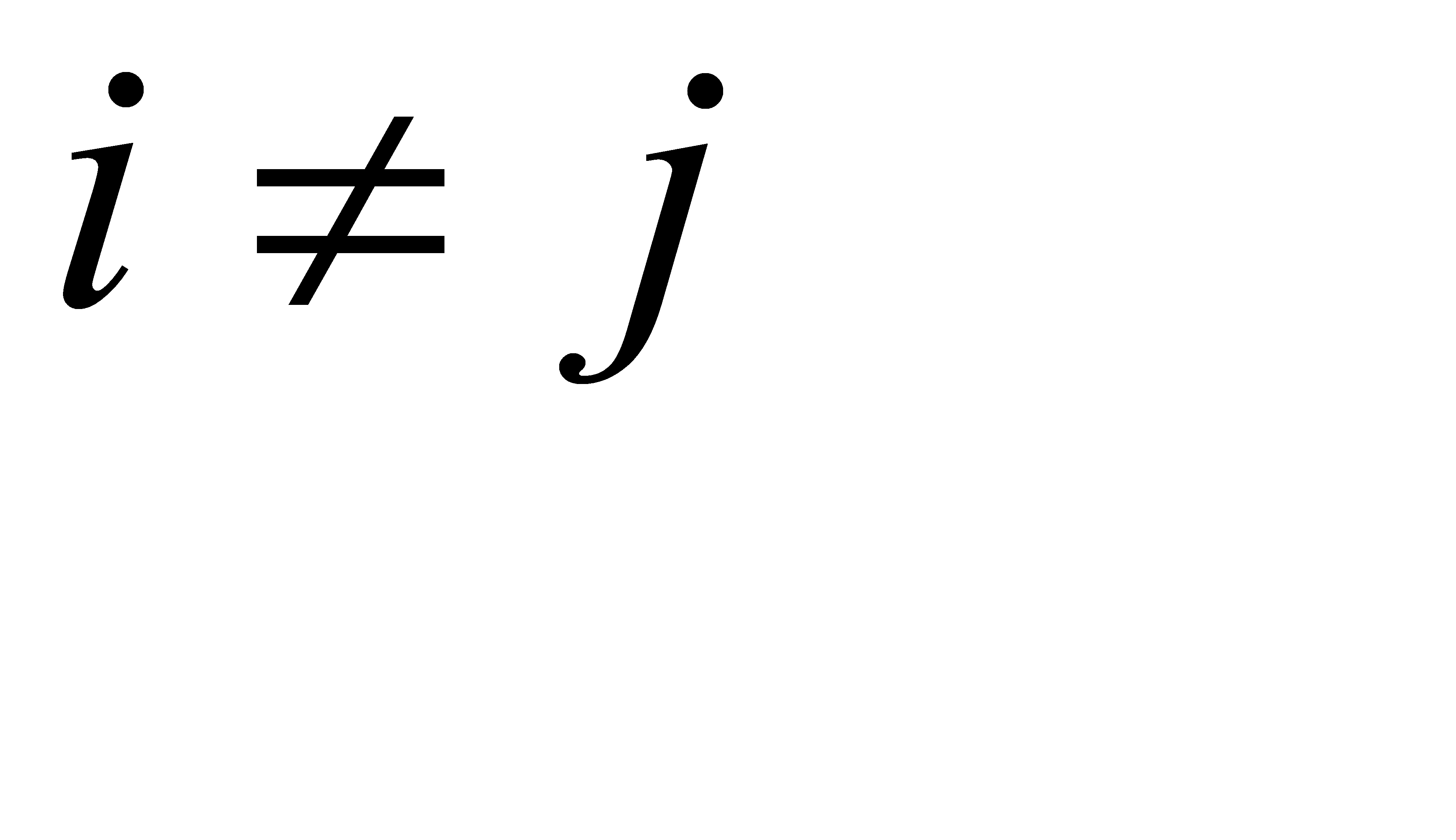 и равен
и равен  . Рассматривая j = 1,2 ,…,n, получим систему, эквивалентную исходной:
. Рассматривая j = 1,2 ,…,n, получим систему, эквивалентную исходной: 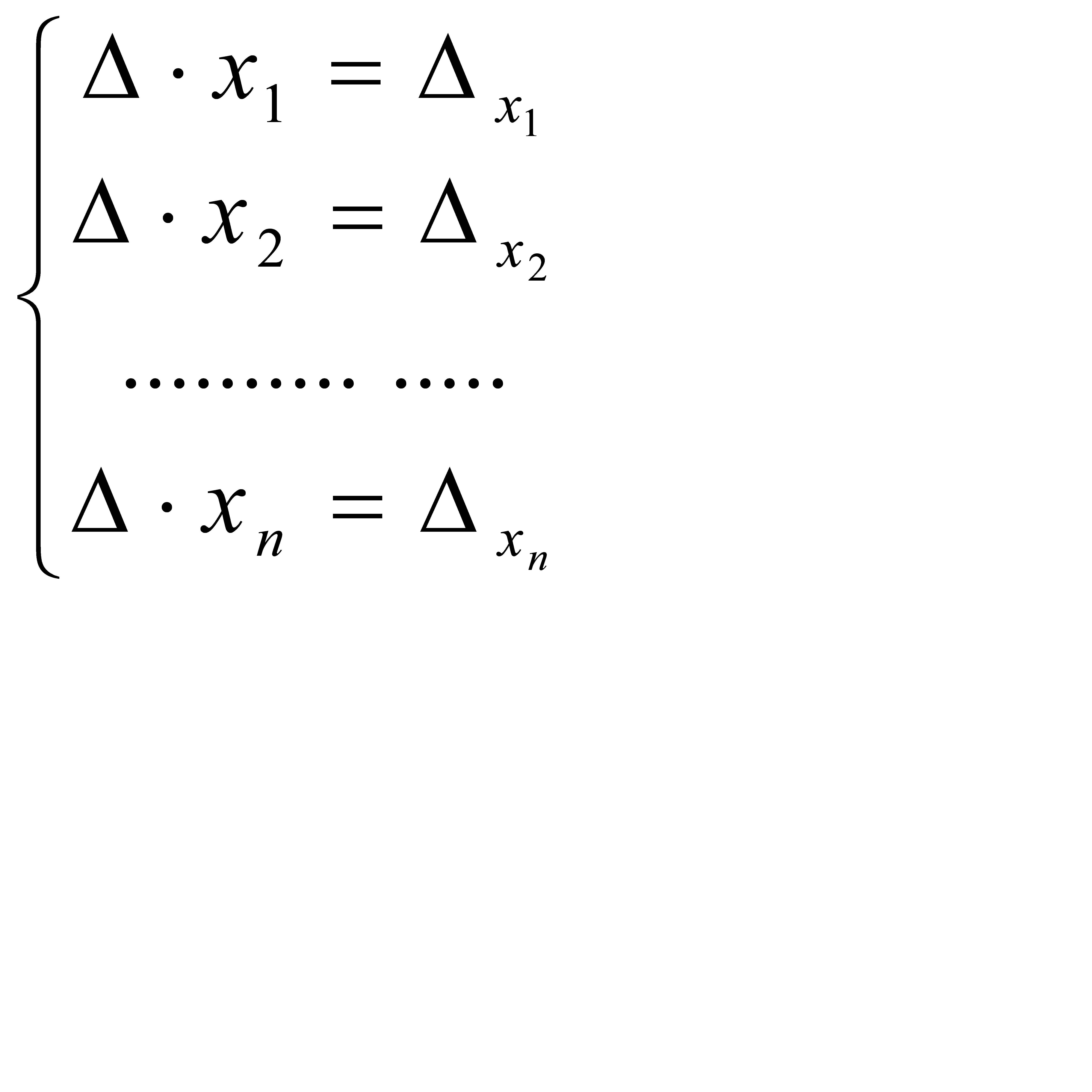 (2.6). Разделив все уравнения на
(2.6). Разделив все уравнения на  .
.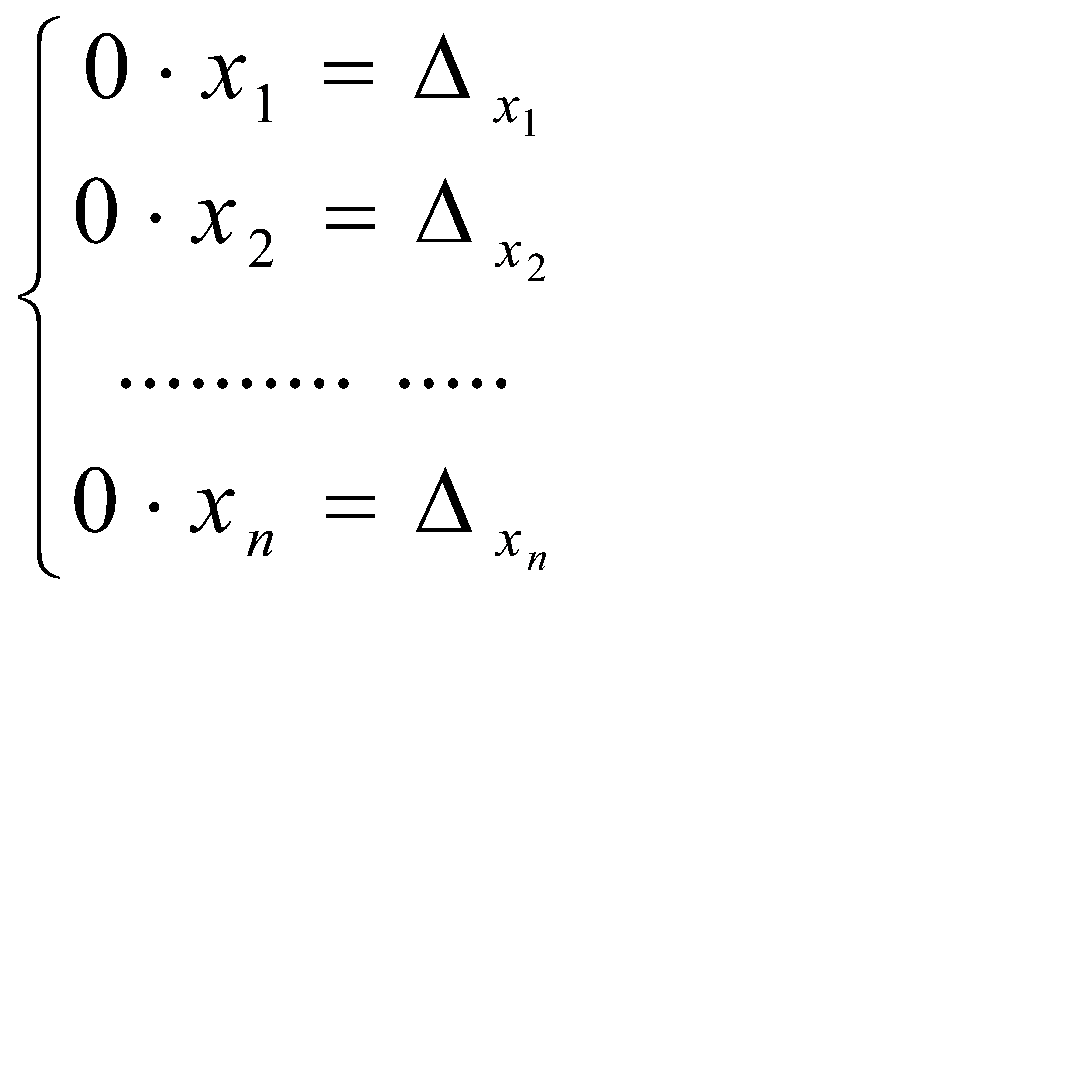 .
. и имеет бесконечно много решений. Если же хотя бы один из
и имеет бесконечно много решений. Если же хотя бы один из  система решений не имеет.
система решений не имеет.
 называется наибольший из порядков миноров матрицы
называется наибольший из порядков миноров матрицы 


 Считаем получаем -2 не равное 0.
Считаем получаем -2 не равное 0.
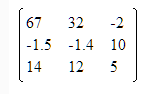


 . В противном случае система не совместна.
. В противном случае система не совместна.

 .
.

 .
. .
. .
. существует вектор
существует вектор 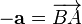 такой, что
такой, что 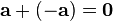 или
или 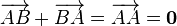 .
.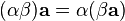 . Умножение вектора на число дистрибутивно относительно сложения чисел:
. Умножение вектора на число дистрибутивно относительно сложения чисел:  .
. .
. .
. , взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов. Любой вектор плоскости
, взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов. Любой вектор плоскости 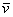 единственным образом раскладывается по базису
единственным образом раскладывается по базису  , где
, где 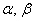 – действительные числа. Числа
– действительные числа. Числа 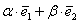 называют разложением вектора
называют разложением вектора 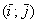 . И это почти так. Формулировка звучит следующим образом:
. И это почти так. Формулировка звучит следующим образом: плоскости, которая называется началом координат, и ортонормированный базис
плоскости, которая называется началом координат, и ортонормированный базис 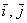
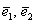 произвольной ненулевой длины. Собственно пример данной системы, всем известной:
произвольной ненулевой длины. Собственно пример данной системы, всем известной:
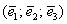 , взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису
, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису 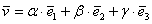 , где
, где 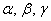 – координаты вектора
– координаты вектора  , взятые в определённом порядке, задают аффинную систему координат трёхмерного пространства:
, взятые в определённом порядке, задают аффинную систему координат трёхмерного пространства:
 задают декартову прямоугольную систему координат пространства.:
задают декартову прямоугольную систему координат пространства.: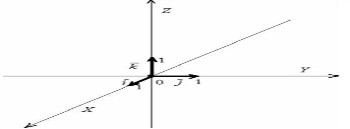
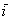 и
и  ортогональны. Ортогональны = Перпендикулярны. Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например:
ортогональны. Ортогональны = Перпендикулярны. Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например:  .Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице. Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например:
.Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице. Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: 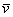 плоскости единственным образом выражается в виде:
плоскости единственным образом выражается в виде: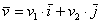 , где
, где 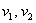 – числа, которые называются координатами вектора в данном базисе. А само выражение
– числа, которые называются координатами вектора в данном базисе. А само выражение 
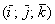 трехмерного пространства и прямоугольная система координат, единичные векторы
трехмерного пространства и прямоугольная система координат, единичные векторы 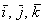 данного базиса попарно ортогональны:
данного базиса попарно ортогональны: 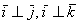 и
и  . Ось
. Ось 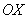 наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. И в данном случае координаты отдельных векторов будут записывать в соответствии с i j k, и вместо отсутствующих координат будут ставить нули. Например 3j – коорд. Y => вектор b (0 3 0).
наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. И в данном случае координаты отдельных векторов будут записывать в соответствии с i j k, и вместо отсутствующих координат будут ставить нули. Например 3j – коорд. Y => вектор b (0 3 0).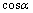 ,
,  ,
, 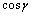 .
.
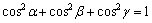 Связь между ними: Это обязательное условие!
Связь между ними: Это обязательное условие!
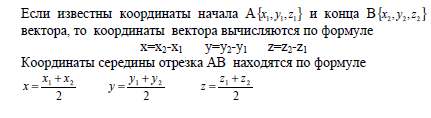
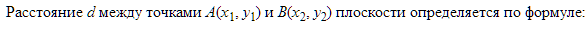
 3. Деление в заданном отношении
3. Деление в заданном отношении




 2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а иb как на сторонах (см. рис. 17), т. е.
2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а иb как на сторонах (см. рис. 17), т. е. 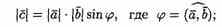




 называется системой векторов.
называется системой векторов. векторов
векторов 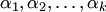 , не все равные нулю одновременно, что
, не все равные нулю одновременно, что
 , т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.
, т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная. тоже образует систему: при
тоже образует систему: при  — линейно зависимую, а при
— линейно зависимую, а при  — линейно независимую.
— линейно независимую. > 0).
> 0). = (А; В) - нормальный вектор прямой.
= (А; В) - нормальный вектор прямой. + С = 0, где
+ С = 0, где  - радиус-вектор произвольной точки на прямой (рис. 4.11).
- радиус-вектор произвольной точки на прямой (рис. 4.11). , его координаты - буквами l, m, n:
, его координаты - буквами l, m, n: .
. прямой и направляющий вектор
прямой и направляющий вектор 

 ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ , параллельного этой прямой.
, параллельного этой прямой. .
. .
. и
и  коллинеарны, поэтому найдётся такое число t, что
коллинеарны, поэтому найдётся такое число t, что 


