
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос37. Первый и второй замечательный пределы и следствия из них.Содержание книги
Поиск на нашем сайте
Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны: Первый замечательный предел:
Второй замечательный предел:
Следствия
Следствия
(а доказательство там-вообще долбанись)
Вопрос38. Сравнение бесконечно малых. Свойства эквивалентных бесконечно малых. И их таблица. Сравнение бесконечно малых функций. Пусть ПРИМЕР 2. Сравнение бесконечно малых функций Эквивалентные бесконечно малые функции. Если Свойства эквивалентных бесконечно малых: 1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них. 2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме. Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак α(x)→0
Вопрос39. Односторонние пределы в точке. Различные определения непрерывности функции в точке. Непрерывность суммы, произведения, частного двух функций. Непрерывность элементарной функции. ОДНОСТОРОННИЕ ПРЕДЕЛЫ
Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что x принимает только значения, меньшие a, то пишут Таким образом, число b называется пределом функции y=f(x) при x→a слева, если каково бы ни было положительное число ε, найдется такое число δ (меньшее a), что для всех Аналогично, если x→a и принимает значения большие a, то пишут Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а. Примеры.
Найдем пределы функции f(x) при x→ 3. Очевидно,
Непрерывность функции в точке. Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Тот же факт можно записать иначе:
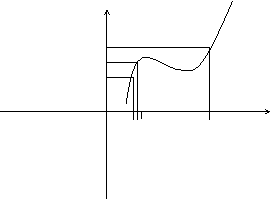
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва. Функциональные ряды Примеры решения задач математика Пример непрерывной функции: y
f(x0)+ f(x0) f(x0)-
0 x0- x0 x0+ x
y
f(x0)+ f(x0) f(x0)- x0 x
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию верно неравенство
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + (x) где (х) – бесконечно малая при хх0.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.130 (0.006 с.) |






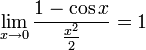

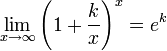


 для
для  ,
, 

 и
и  — две функции, бесконечно малые в точке
— две функции, бесконечно малые в точке  . Если
. Если 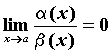 , то говорят, что
, то говорят, что 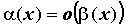 . Если же
. Если же  , то
, то  . Бесконечно малые функции
. Бесконечно малые функции  , обозначают
, обозначают  . И, наконец, если
. И, наконец, если  не существует, то бесконечно малые функции
не существует, то бесконечно малые функции  , то бесконечно малые функции
, то бесконечно малые функции 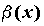 .
. мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.
мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений. До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.
До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов. и называют bпределом функции f(x) в точке a слева.
и называют bпределом функции f(x) в точке a слева. выполняется неравенство
выполняется неравенство  .
. и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех
и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех 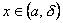 выполняется неравенство
выполняется неравенство  Рассмотрим функцию y=f(x), определенную на отрезке [0,1] следующим образом
Рассмотрим функцию y=f(x), определенную на отрезке [0,1] следующим образом
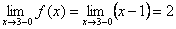 , а
, а  .
.
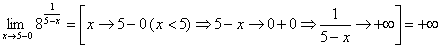 .
. .
.

 Пример разрывной функции:
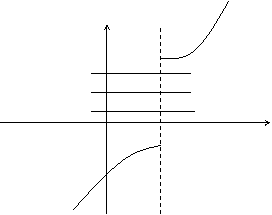
Пример разрывной функции: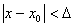
 .
.


