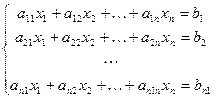Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители высших порядковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим квадратную матрицу размера
Определение 2.2. Определителем (или детерминантом) высшего порядка, соответствующим данной квадратной матрице, называют число, получаемое из элементов матрицы А по определенному закону — закону раскрытия определителя. Это число обозначается
Прежде, чем формулировать закон раскрытия определителей высшего порядка, введем понятие минора и алгебраического дополнения. Определение 2.3. Минором, соответствующим данному элементу определителя n-го порядка, называется определитель (n-1)-го порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Миноры обозначаются буквой Мij с индексами, соответствующими вычеркнутым номерам строк и столбцов. Так, например, минор М12, соответствующий элементу а12 определителя (2.4), есть определитель
Он получается из определителя (2.4) вычеркиванием первой строки и второго столбца. Определение 2.4. Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, в которых стоит элемент, четна, и со знаком минус, если эта сумма нечетна. Алгебраическое дополнение элемента аij обозначается через Aij. Здесь i означает номер строки, а j —номер столбца, на пересечении которых находится данный элемент. Связь между алгебраическим дополнением элемента и его минором выражается следующим равенством:
Определение 2.5. Определитель квадратной матрицы равен сумме попарных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения:
Определение 2.6. Матрица называется невырожденной, если ее определитель отличен от нуля. В качестве примера использования формул (2.7) и (2.8) приводятся формулы разложения определителя третьего порядка
по элементам первой строки
и элементам второго столбца
Поработаем с формулой (2.10) и раскроем миноры по формуле (3.2):
Итак, раскрыв скобки, получим.
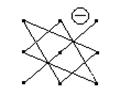
Для запоминания правила вычисления определителя третьего порядка используют модель Саррюса, которая приведена на рис. 2.1. Элементы определителя изображены точками. Перемножают элементы, соединенные линиями, и полученные произведения складывают, снабдив их соответствующими знаками.
Пример 2.2. Вычислить определитель третьего порядка для матрицы:
Воспользуемся формулой (2.7) и раскроем определитель, например, по элементам третьей строки (i=3):
Предварительно вычислим алгебраические дополнения:
Подставим полученные числовые значения алгебраических дополнений в формулу (3.14) и вычислим определитель
Полученное решение можно проверить по формуле (2.12).
Свойства определителей Сформулируем основные свойства определителя:
Обратная матрица Понятие обратной матрицы вводится только для квадратных матриц. Определение 3.3. Если А — квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая А -1и удовлетворяющая условию
Теорема 3.1. (об обратной матрице): Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы ее определитель был отличен от нуля. Для простоты на примере матрицы третьего порядка приведем последовательность вычислений, которая позволяет построить обратную матрицу. Пусть
Невырожденная матрица, т. е. её определитель
Составим новую матрицу В, заменяя в матрице А каждый ее элемент аij его алгебраическим дополнением Аij, деленным на определитель |A | матрицы А:
Построим матрицу ВТ, транспонированную по отношению к матрице В:
Покажем, что матрица ВТ, является обратной матрице А. Для этого составим произведение:
Так как. числители элементов на главной диагонали равны |A| (раскрытие определителя по элементам строки), а числители всех остальных элементов равны нулю (сумма произведений элементов одной строки или столбца на алгебраические дополнения другой строки или столбца равна нулю). Таким образом,
Пример 3.1. Дана матрица
Найти обратную матрицу. Вычислим определитель матрицы А:
Находим алгебраические дополнения элементов этого определителя по формулам
Следовательно,
11.Элементарные преобразования матриц При вычислении обратной матрицы, как правило, приходится вычислять большое число определителей. Чтобы облегчить этот процесс, применяют специальные приемы, которые называют элементарными преобразованиями матриц. Элементарными называются следующие преобразования: · умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля; · прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число; · перемена местами строк (столбцов) матрицы; · отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю. Матрицы, получающиеся одна из другой при элементарных преобразованиях, называются эквивалентными. Пример 4.1. Вычислить определитель матрицы:
Преобразуем матрицу так, чтобы не вычислять много миноров. Для этого в первом столбце во второй, третьей и четвертой строках получим нули. Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на
Теперь к третьей строке прибавим первую строку, умноженную на
И, наконец, к четвертой строке прибавим первую, умноженную на
Определитель полученной матрицы равен произведению элемента
Пример 4.2. Вычислить определитель матрицы:
Преобразуем матрицу так, чтобы под главной диагональю стояли нули. ПоДля этого в первом столбце во второй, третьей и четвертой строках получим нули. Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на
Теперь к третьей строке прибавим первую строку, умноженную на
И, наконец, к четвертой строке прибавим первую, умноженную на Ранг матрицы Рассмотрим матрицу размера
Выделим в ней несколько миноров. Определение 3.1. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Определение 3.2. Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Пример 4.4. Найти ранг матрицы:
Определитель матрицы (3.2) равен нулю. Все миноры 3-го порядка равны нулю, например:
Есть минор 2-го порядка, отличный от нуля:
Значит, Свойства ранга матрицы
Использование этих свойств позволяет в ряде случаев упростить вычисления ранга.
Пример 4.5. Найти ранг матрицы:
Определитель матрицы (4.3) равен нулю, поскольку матрица имеет пропорциональные строки, например, первую и третью. Значит ранг матрицы (4.3) будет меньше 4. Выполним некоторые элементарные преобразования: к третьей строке матрицы прибавим первую строку, умноженную на
Полученная матрица, очевидно, имеет ранг 2. Итак, Метод окаймления При вычислении ранга можно использовать метод окаймления, состоящий в следующем. Пусть матрица Пример 4.6. Найти ранг матрицы, используя метод окаймления:
Эта матрица имеет ненулевой минор
Теперь достаточно рассмотреть не все миноры третьего порядка, а только миноры, которые содержат указанный ненулевой минор второго порядка:
Итак, Система линейных уравнений Система n линейных алгебраических уравнений с n неизвестными имеет следующий вид:
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения. Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет бесчисленное множество решений. Две совместные системы уравнений называются равносильными, если решение первой системы является решением второй и наоборот. С помощью теорем линейной алгебры можно доказать, что следующие преобразования, которые принято называть элементарными, приводят к равносильным системам: · перемена местами двух любых уравнений; · умножение обеих частей уравнений на произвольное число, отличное от нуля; · прибавление к обеим частям одного из уравнений другого уравнения, умноженного на любое действительное число.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


 .
.
 .
.
 .
.
 .
.
 для любых i
для любых i
 для любых j.
для любых j.




 .
.
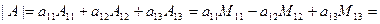










 .
.
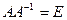







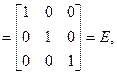
 откуда
откуда  Итак, способ построения обратной матрицы получен:
Итак, способ построения обратной матрицы получен: .
.






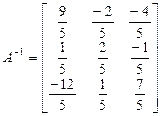


 :
:

 :
: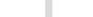

 :
:
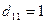 на его алгебраическое дополнение:
на его алгебраическое дополнение:



 .
.



 .
. .
.

 имеет ненулевой минор порядка
имеет ненулевой минор порядка  .Тогда можно рассматривать только миноры порядка
.Тогда можно рассматривать только миноры порядка  , которые содержат упомянутый ненулевой минор порядка
, которые содержат упомянутый ненулевой минор порядка  .
.