
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение системы линейных уравнений матричным методомСодержание книги
Поиск на нашем сайте
Обозначим через А матрицу, составленную из коэффициентов при неизвестных:
Через X — матрицу-столбец, составленную из неизвестных:
Через В — матрицу-столбец, составленную из свободных членов:
Произведение
Тогда система линейных уравнений может быть записана в матричном виде:
Если матрица А системы невырожденная, т. е. · умножаем обе части уравнения на матрицу
· используя сочетательный закон умножения матриц, можно записать:
· так как
Пример 4.1. Решить матричным способом систему уравнений
В матричной форма эта система запишется в виде
Матрица
Решение системы записываем в виде:
Отсюда следует, что Формулы Крамера Рассмотрим еще раз систему n уравнений с n неизвестными
Или
Вспомним, что две матрицы равны, если равны их соответствующие элементы:
Обратим внимание на то, что выражения в круглых скобках равенств (4.13) представляют собой определители, полученные из определителя системы
С учетом этих обозначений формулы (4.13) можно переписать в виде:
Пример 4.2. Решить систему уравнений методом Крамера
Ранее определитель системы
уже был вычислен Вычислим определители неизвестных:
Используя формулы Крамера, найдем:
Множества. Основные понятия Понятие множества является основным, неопределяемым понятием, поэтому можно только пояснить этот термин. Под множеством
Символом Определение 1.1. Множества Записать утверждение о том, что множество
Если множества состоят из разных элементов, то этот факт записывают
Пример 1.1. Даны три множества Пример 1.2. Даны два множества При рассмотрении способов задания множеств возникает проблема их эффективного описания. Частично эту проблему можно решить, если указывать условие, которому удовлетворяет любой элемент данного множества:
Пример 1.3. Множество Зачем? Пример 1.4. Парадокс брадобрея. Владелец парикмахерской в одном селе повесил следующее объявление: «Брею тех и только тех жителей села, кто не бреется сам». Спрашивается, кто бреет брадобрея? Этот парадокс свидетельствует о том, что широко используемая теория множеств в ее интуитивном, «наивном» изложении является противоречивой. Формализация теории множеств, связанная, в частности, с устранением парадоксов, способствовала развитию не только методов теории множеств, но и такой науки, как математическая логика. Определение 1.2. Если все элементы множества А принадлежат также множеству В, причем
Определение 1.3. Если каждый элемент множества А есть элемент множества В, причем возможно
Множество, не содержащее элементов, называется пустым, и обозначается символом Ø. Пустое множество есть подмножество любого множества. Множества бывают конечные и бесконечные. Конечные множества содержат конечное число элементов. Множества, не являющиеся конечными, называются бесконечными. Число элементов конечного множества называется его мощностью. Мощность множества Пример 1.6. Дано множество
Множество всех подмножеств множества Пример 1.7. Дано множество
Операции над множествами Рассмотрим методы получения новых множеств их уже существующих. Определение 1.4. Пересечением множеств А и В называется множество С, состоящее из всех элементов, одновременно входящих и в множество А, и во множество В. Это записывается следующим образом:
Пример 1.7. Если множество А есть интервал (1; 5) а множество В есть интервал (2; 7), то пересечение множеств А и В есть интервал (2; 5): Определение 1.5. Объединением множеств А и В называется множество С, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств или А, или В, или А и В одновременно. Это обозначается следующим образом:
Пример 1.8. Если множество А есть отрезок [1; 3] а множество В есть отрезок [2; 5], то объединение множеств А и В есть отрезок [1; 5]: Определение 1.6. Дополнением множества А называется множество всех элементов универсального множества U, каждый из которых не принадлежит множеству А. Дополнение множества А будем обозначать через
Пример 1.9. Если множество А есть отрезок [1; 3], то множество Определение 1.7. Разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих В:
Пример 1.10. Если множество А есть отрезок Определение 1.8. Симметрической разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множествам А и B, но не принадлежащих ихобщим областям.
Пример 1.11. Если Определение 1.9. Декартовым произведением двух множеств А и В называется множество С, состоящее из всевозможных пар элементов
Пример 1.12. Даны два множества: Из примера видно, что множества
. Тождества теории множеств. То́ждество (в математике) — равенство, выполняющееся на всём множестве значений входящих в него переменных (равенство, верное при любых значениях переменных), Запишем еще раз некоторые свойства операций с множествами:
21 .Множество N натуральных чисел Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). Существуют два подхода к определению натуральных чисел — числа, используемые при:
Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются. Множество всех натуральных чисел принято обозначать знаком Натуральные числа - числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления), т.е натуральные числа - это естественные числа. Всего существуют два подхода к пониманию натуральных чисел- это числа, используемые при: 23. Счетные и несчетные множества.
В теории множеств, счётное мно́жество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формально: множество Счётное множество является «наименьшим» бесконечным множеством, то есть в любом бесконечном множестве найдётся счётное подмножество. Мощность множества всех натуральных чисел обозначается символом Свойства
Связанные понятия Несчётное множество — такое бесконечное множество, которое не является счётным. Таким образом, любое множество является либо конечным, либо счётным, либо несчётным. Примеры Счётные множества
Несчётные множества
24..Множество Q рациональных чисел Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.215.149 (0.01 с.) |




 есть матрица-столбец:
есть матрица-столбец:


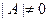 , то система уравнений (5.7) решается следующим образом:
, то система уравнений (5.7) решается следующим образом: , обратную матрице А:
, обратную матрице А:

 , а
, а  решение матричного уравнения получится в виде:
решение матричного уравнения получится в виде: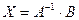




 .
.


 заменой соответствующего номеру неизвестного столбца столбцом свободных членов данной системы уравнений (4.1). Обозначим их следующим образом:
заменой соответствующего номеру неизвестного столбца столбцом свободных членов данной системы уравнений (4.1). Обозначим их следующим образом:




 (пример 4.1).
(пример 4.1).





 понимается собрание определенных и различимых между собой объектов, мыслимое как единое целое.
понимается собрание определенных и различимых между собой объектов, мыслимое как единое целое.

 обозначается отношение принадлежности. Запись
обозначается отношение принадлежности. Запись  означает, что элемент
означает, что элемент  является элементом множества
является элементом множества  .
. и
и  считаются равными, если они состоят из одних и тех же элементов.
считаются равными, если они состоят из одних и тех же элементов.

 ,
, 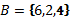 и
и  . В силу того, что все три множества состоят из одних и тех же элементов, справедлива запись
. В силу того, что все три множества состоят из одних и тех же элементов, справедлива запись  .
. и
и  . Эти множества нельзя считать равными, так как единственным элементом множества
. Эти множества нельзя считать равными, так как единственным элементом множества 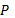 есть множество
есть множество  , множество
, множество  состоит из двух элементов: чисел 1 и 2.
состоит из двух элементов: чисел 1 и 2.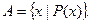
 содержит один элемент:
содержит один элемент:  состоит из набора элементов
состоит из набора элементов 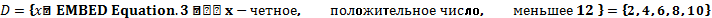 .
.


 , и
, и  . Для этих множеств справедливо
. Для этих множеств справедливо  , поскольку множество
, поскольку множество  включает множество
включает множество 
 .
. . Тогда
. Тогда  . Если множество
. Если множество  элементов, то множество
элементов, то множество  . Множество-степень содержит следующие подмножества:
. Множество-степень содержит следующие подмножества:

 (коммутативность);
2.
(коммутативность);
2.  (ассоциативность);
3.
(ассоциативность);
3.  ;
4.
;
4.  ;
5.
;
5.  Ø = Ø.
Ø = Ø.

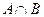
 .
.
 (коммутативность);
2.
(коммутативность);
2.  (ассоциативность);
3.
(ассоциативность);
3.  (дистрибутивность);
4.
(дистрибутивность);
4.  ;
5.
;
5.  ;
6.
;
6.  Ø = Ø.
Ø = Ø.


 .
.
 ;
2.
;
2. 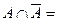 Ø
3.
Ø
3. 

 .
. .
.
 .
Из определения разности множеств следует, что имеет место равенство
.
Из определения разности множеств следует, что имеет место равенство  .
.


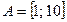 , а множество В есть отрезок
, а множество В есть отрезок  , то разность
, то разность  представляет собой полуинтервал
представляет собой полуинтервал  , а
, а  полуинтервал
полуинтервал  .
.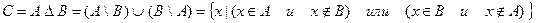 .
.





 ,
,  , то
, то 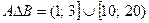 .
. , у которых
, у которых 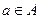 и
и 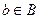 .
.
 ,
,  . Для этих множеств можно составить два варианта декартового произведения этих множеств:
. Для этих множеств можно составить два варианта декартового произведения этих множеств:  и
и 
 и
и  различны.
различны. ,на некоторой прямой, а множество В есть отрезок
,на некоторой прямой, а множество В есть отрезок  другой прямой. Тогда декартово произведение
другой прямой. Тогда декартово произведение  , включающее многочисленные пары координат, составит прямоугольник на плоскости.
, включающее многочисленные пары координат, составит прямоугольник на плоскости.









 . Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.
. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число. является счётным, если существует биекция
является счётным, если существует биекция  , где
, где  обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.
обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел. (произносится: "алеф-нуль")
(произносится: "алеф-нуль") , числитель
, числитель  — целое число, а знаменатель
— целое число, а знаменатель  — натуральное число, к примеру 1/4. Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые вещи (длину, вес, площадь и т.п.), люди поняли, что не удаётся обойтись целыми числами и необходимо ввести понятие доли: половины, трети и т.п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки.
— натуральное число, к примеру 1/4. Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые вещи (длину, вес, площадь и т.п.), люди поняли, что не удаётся обойтись целыми числами и необходимо ввести понятие доли: половины, трети и т.п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки.


