
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример. Число
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой. Пример. Число
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему. Пример 1. Число
Пример 2. Число
29.Комбинаторика Правило умножения Элементы комбинаторики Пусть имеется n различных объектов произвольной природы. Выберем из них к объектов. Комбинаторика - это раздел математики, который изучает, сколькими способами можно осуществить этот выбор согласно заданным условиям. Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике). Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Правило умножения Если объект А можно выбрать к1 различными способами, а объект В - к2 различными способами, то пару объектов А и В можно выбрать к1 · к2 различными способами. Другая интерпретация этого правила такова. Пусть первое действие можно совершить к1 различными способами, второе – к2 различными способами. Тогда оба действия можно совершить к1 · к2 различными способами. Пример 1. Пусть из пункта A в пункт B имеется 5 дорог, а из пункта B в пункт C - 6 дорог. 1) Сколько существует различных вариантов проезда из пункта A в пункт C? 2) Сколько существует различных вариантов проезда из пункта A в пункт B и обратно? 3) Сколько существует различных вариантов проезда из пункта A в пункт B и обратно при условии, что дороги туда и обратно будут разными? Решение. 1) Существует 5 различных путей из пункта A в пункт B - это 5 способов выполнения первого действия, при этом существует 6 различных путей из пункта B в пункт C - это 6 различных способов выполнения второго действия. Согласно правилу умножения, число различных способов выбора пути из пункта A в пункт C равно 5·6 = 30.
2) Из пункта A в пункт B ведет 5 дорог, значит, имеется 5 способов проезда туда и 5 способов проезда обратно. По правилу умножения число всех способов проезда туда и обратно равно 5·5 = 25. 3) Рассуждаем аналогично пункту 2), но учитываем, что дороги туда и обратно не должны совпадать, т.е. при выборе одного из 5-ти способов проезда «туда» обратно можно вернуться одним из 4-х способов. Поэтому число различных способов проехать из пункта A в пункт B и вернуться обратно, но обязательно другой дорогой, равно 5·4 = 20. Пример 2. В урне находятся 10 белых, 15 синих и 20 красных карточек. Вынимают три карточки и выкладывают их одну над другой. Сколькими различными способами можно это сделать, чтобы карточки расположились в порядке цветов российского флага? Решение. В таких задачах предполагается, что все карточки различимы, например, перенумерованы. Тройку карточек можно образовать тремя действиями. 1- е действие. Возьмем одну красную карточку. Это действие можно совершить 20-ю способами (по числу различных красных карточек в урне). 2- е действие. К красной карточке добавим сверху синюю, которую можно взять 15-ю различными способами (по числу различных синих карточек в урне). 3- е действие. К выбранной паре присоединим сверху белую карточку, которую можно взять 10-ю различными способами (по числу белых карточек в урне). Число различных способов выбора равно 20·15·10 = 3 000 Пример 3. В меню ресторана 5 первых блюд, 10 вторых и 7 третьих. Сколько различных вариантов меню можно составить? Решение. Первое блюдо можно выбрать пятью способами, второе - десятью, а третье - семью. Значит, общее количество способов составляет 5·10·7 = 350. 30.Комбинаторика Правило суммы
Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Правило сложения Если объект А можно выбрать к1 различными способами, а объект В - к2 различными способами, то выбрать один объект А или В можно к1 + к2 различными способами. Пример 4. В ящике лежат 2 красных, 3 зелёных и 4 чёрных шара. Сколькими способами можно выбрать цветной шар? Решение. Выбрать цветной шар - значит выбрать красный или зелёный шар. Количество способов равно 2 + 3 = 5.
31.Формулы включения-исключения
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.50.186 (0.011 с.) |

 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.
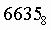 перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.



