Двоичные деревья. Таблицы и реализация дерева поиска.

Двоичные деревья.

Определение и построение

 

Связанный граф, в котором нет циклов, называется деревом. Дерево называется ориентированным, если на каждом его ребре указано направление.

 

Двоичное дерево - это такое ориентированное дерево, в котором:

 

1) Имеется ровно одна вершина, в которую не входит ни одного ребра. Эта вершина называется корнем двоичного дерева.

 

2) В каждую вершину, кроме корня, входит одно ребро.

 

3) Из каждой вершины исходит не более двух ребер.

 

Будем изображать двоичные деревья так, чтобы корень располагался выше других вершин.

 

Для ребер, выходящих из любой вершины, имеется две возможности - быть направленными влево вниз и вправо вниз. При этом, если из вершины выходит одно ребро, то указание направления ребра влево вниз или вправо вниз является существенным. При таких соглашениях нет необходимости указывать направление на ребрах - все ребра ориентированы вниз.

 

При решении некоторых задач бывает удобно представить наборы объектов в виде двоичных деревьев.

 

Рассмотрим задачу кодирования непустой последовательности целых чисел.

Пусть дана последовательность целых чисел а1, …, аn и функция целочисленного аргумента F(x), принимающая целые значения. Значение F(x) будем называть кодом числа x. Пусть требуется закодировать данные числа, т.е. вычислить значения F(a1),..., F(an), и пусть в последовательности a1,..., an имеются частые повторения значений элементов.

 

Чтобы избежать повторных вычислений одного и тоже же значения, следует по ходу кодирования строить таблицу уже найденных кодов. Организация этой таблицы должна быть такой, чтобы, во-первых, в ней довольно быстро можно было находить элементы с данным значением (или устанавливать факт отсутствия его в таблице), и, во-вторых, без особых затрат добавлять в таблицу новые элементы.

 

Этим требованиям удовлетворяет представление таблицы в виде двоичного дерева, в вершинах которого расположены различные элементы из данной последовательности и их коды.

 

Процесс построения двоичного дерева идет так: первое число и его код образуют корень. Следующее число, которое нужно кодировать, сравнивается с числом в корне, и если они равны, то дерево не разрастается и код может быть взят из корня. Если новое число меньше первого, то про-водится ребро из корня влево вниз, иначе - вправо вниз. В образовавшуюся вершину помещаются это новое число и его код.

 

Пусть уже построено некоторое дерево и имеется некоторое число x, которое нужно закодировать. Сначала сравниваем с x число из корня. В случае равенства поиск закончен, и код x извлекается из корня. В противном случае переходим к рассмотрению вершины, которая находится слева внизу, если x меньше только что рассмотренного, или справа внизу, если x больше рассмотренного. Сравниваем x с числом из этой вершины и т.д. Процесс завершается в одном из двух случаев:

 

1) Найдена вершина, содержащая число x.

2) В дереве отсутствует вершина, к которой надо перейти для выполнения очередного шага поиска.

 

В первом случае из найденной вершины извлекается код числа x. Во втором необходимо вычислить F(x) и присоединить к дереву вершину, в которой расположены x и F(x). Пусть последовательность начинается с чисел 8, 4, 13, 10, 14, 10. Тогда вначале дерево будет разрастаться следующим образом (рис. 9а-д):

Рис. 9. Разрастание двоичного дерева в задаче кодирования

При появлении числа 10 в качестве шестого элемента последовательности к дереву не добавляется новой вершины, а значение F(10) извлекается из имеющейся вершины (рис. 9д).

 

Определим в программе построения последовательности кодов следующую структуру:

 

struct node {

int num, code;

node* left, * right;

node (int n, int c, node *l, node *r){

num = n; code = c;

left = l; right = r; } };

Объекты типа node являются структурами, в которых в каждое из полей left и right есть либо NULL, либо указатель на место в памяти, отведенное с помощью new для объекта типа node. Дерево можно представить в виде множества объектов типа node, связанных указателями. Сами эти объекты будут вершинами дерева, а указатели на места в памяти, отведенные для объектов типа node, - ребрами дерева. Если при этом поле left (right) есть NULL, то это значит, что в дереве из данной вершины не исходит ребро, направленное влево вниз (вправо вниз). Изобразим на рис. 10 представление дерева, соответствующего рис. 9д, в памяти ЭВМ:

Рис. 10. Изображение дерева в памяти ЭВМ

. Выполнение присваивания v = v->left (v = v->right) означает переход к вершине, расположенной непосредственно слева снизу (справа снизу) от данной, если, конечно, соответствующее поле данной вершины не есть NULL. Таким способом можно передвигаться от вершины к вершине сверху вниз. Включение новой вершины в дерево представляет собой изменение значений полей типа node* некоторых вершин данного дерева.

 

Вместе с каждым деревом рассматривается переменная, значением которой является указатель на корень дерева. Если в дерево не входит ни одной вершины, значение этой переменной должно равняться нулевому указателю NULL.

 

Напишем программу, по ходу выполнения которой кодируется последовательность натуральных чисел, расположенных во входном файле NUM.DAT. Для кодирования используем файл COD.DAT, компонентами которого являются целые числа. Кодом F(k) числа k будем считать k-ю по порядку компоненту файла COD.DAT.

 

struct node {

int num, code;

node* left, *right;

node (int n, int c, node* l, node* r){

num = n; code = c; left = l; right = r;}

};

int f(int);

void insert(int n, node* root){

node*temp = root;

node* old;

while (temp!=0) {

old = temp;

if (temp->num = = n) { cout << temp->code <<" "; return; }

if (temp->num > n) temp = temp->left;

else temp = temp->right;

}

int k = f(n); cout << k << " ";

if (old->num > n) old->left = new node(n, k, 0, 0);

else old->right = new node(n, k, 0, 0);

}

ifstream num ("num.dat"), cod ("cod.dat");

int f(int k) { int i, j;

cod.seekg(0); // Устанавливает позицию чтения из файла в 0.

for (i = 1; i <=k; i++) cod >> j;

return j;

}

 

void main(){

int n;

num >> n;

node* root = new node (n, f(n), 0, 0); cout << root->code << " ";

while (num.peek()!= EOF){ num >> n;

insert (n, root);

}}

Таблицы и реализация дерева поиска.

Построенное в последнем примере дерево часто называют деревом поиска. Дерево поиска иногда используют для построения таблиц, в которых хранятся различные сведения, обычно в виде структур. При этом для упорядочения структур они обычно именуются и чтобы организовать эффективный поиск структуры по ее имени, нужно иметь возможность сравнивать любые два имени и устанавливать, какое из них "больше", а какое -"меньше". Имя структуры в таблице часто называют ключом структуры. В качестве ключа часто используют целые числа или строки одинаковой длины.

 

Над таблицей как структурой данных определены операции:

· поиск в таблице структуры с заданным ключом;

· включение в таблицу структуры с заданным ключом;

· исключение из таблицы структуры с заданным ключом.

 

Мы рассмотрим организацию таблиц в виде двоичного дерева. В примере кодирования ключом служили сами числа из файла NUM.DAT. Фактически мы уже рассмотрели операции поиска в дереве и включения элемента в дерево по заданному ключу. Сейчас оформим в виде функции операцию исключение элемента с заданным ключом из дерева.

 

Непосредственное удаление структуры реализуется просто, если удаляемая вершина дерева является конечной или из нее выходит только одна ветвь (рис. 11):

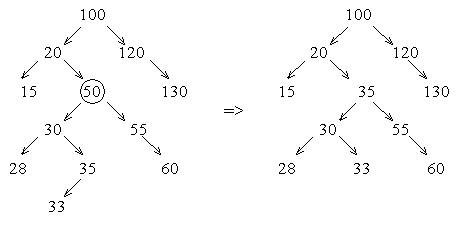
Рис. 11. Удаление элемента из дерева, когда удаляемая вершина

является конечной или из нее выходит только одна ветвь

Трудность состоит в удалении вершины, из которой выходят две ветви. В этом случае нужно найти подходящее звено дерева, которое можно было бы вставить на место удаляемого, причём это подходящее звено должно просто перемещаться. Такое звено всегда существует: это либо самый правый элемент левого поддерева, либо самый левый элемент правого поддерева. В первом случае для достижения этого звена необходимо перейти в следующую вершину по левой ветви, а затем переходить в очередные вершины только по правой ветви до тех пор, пока очередной указатель не будет равен NULL. Во втором случае необходимо перейти в следующую вершину по правой ветви, а затем переходить в очередные вершины только по левой ветви до тех пор, пока очередной указатель не станет равен NULL. Такие подходящие звенья могут иметь не более одной ветви. Ниже (рис. 12) схематично изображено исключение из дерева вершины с ключом 50:

Рис. 12. Исключение из дерева вершины с ключом 50

. Приведём программу, реализующую дерево поиска со всеми операциями с помощью класса tree и несколько изменённой функции insert.

 

#include < fstream.h>

 

struct node {

int key, code;

node *left, *right;

node (int k, int c, node *l, node *r){ key = k; code = c; left = l; right = r; }

};

int f(int);

class tree {

node *root;

void print (node *r); // Печать с указателя r.

public:

int insert (int);

void del (int);

tree () { root = 0; } // Создание пустого дерева.

node *&find (node *&r, int key); // Поиск элемента в поддереве

// с вершиной r.

node *&find (int key) { // Поиск по всему дереву.

return (find(root, key));

}

void print () { print (root); } // Печать всего дерева.

};

int tree::insert (int key){ // Возвращает код.

node* t = root;

node* old;

int k;

if (root = = 0) { k = f(key);

root = new node(key, k, 0, 0);

return k;

}

while (t!=0){

old = t;

if (t-> key = = key){

return t->code; }

if (t->key > key) t = t->left;

else t = t->right; }

k = f (key);

if (old->key > key) old->left = new node (key, k, 0, 0);

else old->right = new node (key, k, 0, 0);

return k; }

node *&tree::find (node *&r, int key){ // Рекурсивная функция

if (r = = 0) return r; // поиска в поддереве r.

if (r->key = = key) return r;

if (r->key > key) return (find (r->left, key));

else

return (find (r->right, key));

}

void del_el (node *&r, node *q){ // Рекурсивная функция

if (r->right = = 0) { // удаления элемента,

q->key = r->key; // на который указывает q.

q->code = r->code;

q = r; r = r-> left;

} else

del_el (r->righ, q);

}

void tree::del (int key){ // Удаление элемента с ключом key.

{ node *&q = find (key); // Установка указателя q на удаляемый

// элемент.

if (q = = 0) { cout << "Элемента с ключом " << key <<" нет\n";

return; }

if (q->right = = 0) q = q->left;

else

if (q->left = = 0) q = q->right;

else

del_el (q->left, q);

}

void print (node *r){ // Глобальная функция печати

// элемента дерева r.

cout << r->key << " " << r->code << " ";

}

void tree::print (node *r) { // Рекурсивная функция печати

if (r!= 0) { // поддерева, начиная с r.

::print (r);

print (r->left);

print (r->right);

}

}

ifstream numb ("num.dat"), cod ("cod.dat");

int f (int k){ int i, j;

cod.seekg (0);

for (i = 1; i <= k; i++) cod >> j;

return j;

}

 

void main (){

cout << "-------------------------------------------------------------------\n";

int key;

tree t;

while (num.peek ()!= EOF) {

numb >> key;

cout << t.insert (key) << " "; // Вставка и печать элемента,

} // или просто печать, если

cout << '\n'; // элемент уже есть.

t.print ();

cout << "\n\n";

key = 50;

t.del (key);

t.print ();

cout << '\n';

}

 

Заметим, что рекурсивная функция del_el вызывается, если из удаляемой вершины направлены два ребра дерева. Она спускается до самого правого звена левого поддерева удаляемого элемента *q, а затем заменяет значения членов key и code в *q соответствующими значениями полей key и code вершины *r. После этого вершину, на которую указывает r, можно исключать с помощью оператора r = r->left. Можно видоизменить эту функцию, освобождая память, занимаемую удалённым звеном с помощью операции delete.
1. Алфавиты и типы данных. Целые и плавающие типы.
2. Выражение присваивания. Арифметические операции с целыми и плавающими переменными.
3. Логические операции, операции автоувеличения и автоуменьшения, тернарная операция.
4. Составной оператор. Условный оператор.
5. Оператор switch - case. Оператор безусловного перехода, break, continue.
6. Операторы цикла. Оператор безусловного перехода, break, continue.
7. Указатели. Указатели и массивы. Адресная арифметика.
8. Символьные массивы и строки. Указатели и многомерные массивы.
9. Операции для работы с динамической памятью.
10. Объявления и определения. Область существования имени.
11. Область видимости имён. Классы памяти.
12. Объявления объектов и типов. Синоним имени типа.
13. Правила преобразования стандартных типов. Неявные преобразования стандартных базовых типов. Преобразования производных стандартных типов.
14. Функции. Передача аргументов. Указатели на функции.
15. Ссылки. Передача аргументов в функции по ссылке.
16. Функции. Аргументы по умолчанию и переопределение функций.
17. Шаблоны функций.
20. Перечисления.
21. Классы. Конструкторы и деструкторы.
22. Статические члены класса.
23. Указатель this. Статические функции-члены.
24. Указатели на члены класса.
25. Конструктор копирования и операция присваивания.
26. Привилегированные функции.
27. Производные классы. Построение. Защищённые классы.
28. Преобразования типов, связь с наследованием.
29. Раннее и позднее связывание. Виртуальные функции.
30. Переопределение стандартных операций.

31. Преобразования абстрактных типов.

32. Классы и шаблоны.

33. Списки. Операции над односвязными списками.

34. Реализация односвязных списков.

35. Двунаправленные и кольцевые списки. Операции над ними.

36. Стеки. Их реализация.

37. Двоичные деревья. Таблицы и реализация дерева поиска.