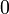Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы включения-исключенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формулы включения-исключения позволяют определить число элементов в объединении нескольких конечных множеств. Рассмотрим случаи двух и трех множеств. Число элементов конечного множества будем обозначать через Тогда для двух конечных множеств А и В справедлива формула,
Справедливость этой формулы можно проиллюстрировать диаграммой Эйлера-Венна.
Для трех конечных множеств А, В и С справедлива формула
Пример 1.14. Порезультатам тестов из 25 слушателей студенческой группы 12 человек показали себя как обладатели веселого характера, 16 — проявили себя как замкнутые и 8 не показали себя ни веселыми, ни замкнутыми. Сколько человек оказались одновременно веселого, но не замкнутого характера? Решение. Пусть А — множество студентов веселого характера, В — множество студентов замкнутого характера, и С — множество студентов не обладающих ни веселым ни замкнутым характером.
Пример 1.14. В бюро переводов работают несколько человек, причем каждый из них знает хотя бы один из трех языков — английский, французский и немецкий. Английский язык знают 12 человек, французский — 10 человек, немецкий — 8 человек, английский и французский — 6 человек, английский и немецкий — 4 человека и французский и немецкий — 2 человека. Все три языка знает один человек. Сколько человек работает в бюро переводов? Сколько из них знает только английский язык? Только французский язык? Только немецкий язык? Решение. Введем следующие множества:
А — множество всех сотрудников, знающих английский язык; В — множество всех сотрудников, знающих французский язык; С — множество всех сотрудников, знающих немецкий язык, D — множество всех сотрудников, знающих английский и французский языки, E — множество всех сотрудников, знающих английский и немецкий языки. Из условия задачи можно записать:
Применяя формулу включения-исключения для трех множеств, получим общее число переводчиков бюро:
Продолжим вычисления:
Применим формулу включения-исключения для двух множеств получим
Итак, английский язык знают 12 человек, из них еще хотя бы один язык знают 9 человек. Поэтому только английский знают Аналогично находим, что французский язык и еще хотя бы один язык знают Только немецкий язык знают
32.Перестановки и размещения Перестановки. Возьмём n различных элементов: a1, a2, a3,…, an. Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается Pn. Это число равно произведению всех целых чисел от 1 до n: Pn = 1·2·3·…·(n-1)·n = n! Символ n! (называется факториал) - сокращённая запись произведения: 1·2·3·…·(n-1)·n Пример: Найти число перестановок из трёх элементов: a, b, c. Решение: В соответствии с приведенной формулой: P3 = 1·2·3 = 6. Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.
Размещения. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются размещениями из n элементов по m. Их общее количество обозначается Anm и равно произведению:
Anm = n(n-1)(n-2)·…·[n-(m-1)] Пример: Найти число размещений из четырёх элементов a, b, c, d по два. Решение: В соответствии с формулой получим: A42=4·3=12 Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.
33.Сочетания Сочетания Пусть имеется множество из n различных объектов (элементов), т.е. объекты имеют или разные названия или разные номера. Пусть к < n, к
Сочетанием из n элементов по к называется любое подмножество, содержащее к элементов, взятых из данных n элементов без учета порядка выбора элементов. При этом подмножества различаются только элементами, входящими в них; порядок, в котором они расположены, не имеет значения. Число различных сочетаний из n элементов по к можно найти по формуле:
Пример 5. Из группы в 25 человек нужно выделить 3 человека на дежурство. Сколькими различными способами это можно сделать? Решение. Исходное множество различных объектов образуют студенты группы. Число всех элементов множества равно 25. Выделенные 3 человека дежурных образуют трехэлементное подмножество из общего числа в 25 элементов (n = 25, к = 3). При этом подмножество определяется только элементами, в него входящими, но не их порядком. Поэтому, по определению имеем сочетание из 25 элементов по 3, и по формуле число различных способов выбрать трех дежурных из 25 студентов равно
Пример 6. В урне находятся 10 белых, 15 черных, 20 красных шаров. Из урны наудачу берутся 9 шаров. Найдите: 1) сколькими различными способами можно вынуть 9 шаров; 2) сколькими различными способами можно взять 9 шаров, среди которых 6 белых и 3 черных; 3) сколькими различными способами можно взять 9 шаров, среди которых 2 белых, 3 черных и 4 красных шара. Решение. 1) Всего в урне 45 шаров. Считаем, что шары различимы, например, пронумерованы. Следовательно, имеем множество из n = 45 различных объектов. Наудачу взятые 9 шаров образуют подмножество из к = 9 элементов. Это подмножество определяется лишь элементами, попавшими в него, порядок не имеет значения. Следовательно, это сочетание из 45 элементов по 9:
2) Взятие 9-ти шаров, из которых 6 белых и 3 черных, можно разбить на два действия: 1-е действие - возьмем 6 белых шаров из 10 белых шаров, находящихся в урне (это можно сделатьС106 различными способами); 2-е действие – возьмем 3 черных шара из общего числа 15 черных шаров (это можно сделатьС103 различными способами). Тогда число различных способов взятия 9-ти шаров нужного состава по правилу умножения равно
3) Чтобы получить 9 шаров, из которых 2 белых, 3 черных и 4 красных, надо последовательно выполнить три действия: а) взять 2 белых шара из общего числа 10 белых шаров; б) взять 3 черных шара из общего числа 15 черных шаров; в) взять 4 красных шара из общего числа 20 красных шаров. Число способов:
Пример 7. В коробке находятся 50 деталей, из которых 10 бракованных. Из коробки наудачу берутся 5 деталей. Найдите число различных способов взятия 5-ти деталей, среди которых ровно 3 бракованных. Решение. Множество состоит из n = 50 различимых деталей, из которых 10 бракованных, 40 доброкачественных. Чтобы получить множество из 5-ти деталей, содержащих 3 доброкачественные, надо совершить последовательно 2 действия: а) взять три бракованные изделия из общего числа 10 бракованных деталей (это действие можно совершить С103 различными способами), б) взять две доброкачественные детали из 40 доброкачественных деталей (это действие можно совершить С402 различными способами). Тогда по правилу умножения оба действия можно совершить:
34.Бином Ньютона Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
где
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд (см. ниже). Биномиальные многочлены Семейство многочленов G называется биномиальным, если оно представляется в виде суммы произведений набора множителей g:
где
Биномиальные многочлены обладают биномиальным разложением:
Биномиальная группа Группа из одномерных матриц
где
Единицей группы является
где
35.Функции и их свойства
Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменная х- независимая переменная или аргумент. Переменная у- зависимая переменная Значение функции- значение у, соответствующее заданному значению х. Область определения функции- все значения, которые принимает независимая переменная. Область значений функции (множество значений)- все значения, которые принимает функция. Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x) Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x) Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2) Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
Способы задания функции ¨ Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-íåêîòîðîå âыðàæåíèå с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически. ¨ На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.
Виды функций и их свойства
1) Постоянная функция- функция, заданная формулой у=b, где b- некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат
2) Прямая пропорциональность- функция, заданная формулой у=kx, где к¹0. Число k называется коэффициентом пропорциональности. Cвойства функции y=kx: 1. Область определения функции- множество всех действительных чисел 2. y=kx - нечетная функция 3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
3) Линейная функция- функция, которая задана формулой y=kx+b, где k и b- действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx. Свойства функции y=kx+b: 1. Область определения- множество всех действительных чисел 2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна. 3. При k>0функция возрастает, а при k<0 убывает на всей числовой прямой Графиком функции является прямая.
4) Обратная пропорциональность- функция, заданная формулой y=k/х, где k¹0 Число k называют коэффициентом обратной пропорциональности. Свойства функции y=k/x: 1. Область определения- множество всех действительных чисел кроме нуля 2. y=k/x- нечетная функция 3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥). Графиком функции является гипербола. 5) Функция y=x2 Свойства функции y=x2: 1. Область определения- вся числовая прямая 2. y=x2 - четная функция 3. На промежутке [0;+¥) функция возрастает 4. На промежутке (-¥;0] функция убывает Графиком функции является парабола.
6) Функция y=x3 Свойства функции y=x3: 1. Область определения- вся числовая прямая 2. y=x3 - нечетная функция 3. Функция возрастает на всей числовой прямой Графиком функции является кубическая парабола 7) Степенная функция с натуральным показателем- функция, заданная формулой y=xn, где n - натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x2; y=x3. Их свойства рассмотрены выше. Пусть n- произвольное четное число, большее двух: 4,6,8... В этом случае функция y=xn обладает теми же свойствами, что и функция y=x2. График функции напоминает параболу y=x2, только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем «теснее прижимаются» к оси Х, чем больше n. Пусть n- произвольное нечетное число, большее трех: 5,7,9... В этом случае функция y=xn обладает теми же свойствами, что и функция y=x3. График функции напоминает кубическую параболу. 8) Степенная функция с целым отрицательным показателем- функция, заданная формулой y=x-n, где n - натуральное число. При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4. Пусть n- нечетное число, большее единицы: 3,5,7... В этом случае функция y=x-n обладает в основном теми же свойствами, что и функция y=1/х. Пусть n- четное число, например n=2. Свойства функции y=x-2: 1. Функция определена при всех x¹0 2. y=x-2 -четная функция 3. Функция убывает на (0;+¥) и возрастает на (-¥;0). Теми же свойствами обладают любые функции при четном n, большем двух.
9) Функция y=Öх Свойства функции y=Öх: 1. Область определения - луч [0;+¥).
2. Функция y=Öх - общего вида 3. Функция возрастает на луче [0;+¥).
10) Функция y=3Öх Свойства функции y=3Öх: 1. Область определения- вся числовая прямая 2. Функция y=3Öх нечетна. 3. Функция возрастает на всей числовой прямой.
11) Функция y=nÖх При четном n функция обладает теми же свойствами, что и функция y=Öх. При нечетном n функция y=nÖх обладает теми же свойствами, что и функция y=3Öх.
12) Степенная функция с положительным дробным показателем- функция, заданная формулой y=xr, где r - положительная несократимая дробь. Свойства функции y=xr: 1. Область определения- луч [0;+¥). 2. Функция общего вида 3. Функция возрастает на [0;+¥). На рисунке изображен график функции y=x5/2. Он заключен между графиками функций y=x2 и y=x3, заданных на промежутке [0;+¥).Подобный вид имеет любой график функции вида y=xr, где r>1. На рисунке изображен график функции y=x2/3. Подобный вид имеет график любой степенной функции y=xr, где 0<r<1
13) Степенная функция с отрицательным дробным показателем-функция, заданная формулой y=x-r, где r - положительная несократимая дробь. Свойства функции y=x-r: 1. Обл. определения -промежуток (0;+¥) 2. Функция общего вида 3. Функция убывает на (0;+¥)
14) Обратная функция Если функция y=f(x) такова, что для любого ее значения yo уравнение f(x)=yo имеет относительно х единственный корень, то говорят, что функция f обратима. Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и областью ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на Y. Таким образом, чтобы построить график функции, обратной к функции y=f(x), надо график функции y=f(x) подвергнуть преобразованию симметрии относительно прямой y=x. 15) Сложная функция- функция, аргументом которой является другая любая функция. Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2. Получается: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.
36.Понятие числовой функции В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел
График функции
Фрагмент графика функции
Примеры
Способы задания функции
Аналитический способ Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента. Примеры:
Табличный способ Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
Графический способ
Осциллограмма задаёт значение некоторой функции графически. Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции. Рекурсивный способ Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения. Примеры:
Словесный способ Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные. Примеры:
Классы числовых функций
37.Основные свойства функции Свойства функции Функция - это одно из важнейших математических понятий. Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции. Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее! Для построения графика функции советуем использовать нашу программу - Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам! Основные свойства функций. 1) Область определения функции и область значений функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. В элементарной математике изучаются функции только на множестве действительных чисел. 2) Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю. 3) Промежутки знакопостоянства функции. Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны. 4) Монотонность функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции. 5) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат. 6) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная. 7) Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы). Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции
38.Схема исследования основных свойств функции
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.206.120 (0.021 с.) |

 .
.


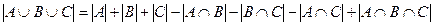


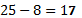 . Обозначим через
. Обозначим через  количество студентов веселого, но не замкнутого характера, тогда
количество студентов веселого, но не замкнутого характера, тогда  . Отсюда
. Отсюда  .
.

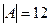 ,
,  ,
, 

 ,
,  ,
, 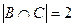


 ,
,  ,
, 
 ,
, 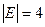 ,
, 

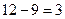 человека.
человека. человек. Поэтому число сотрудников, знающих только французский равно
человек. Поэтому число сотрудников, знающих только французский равно  .
. человек
человек N.
N.




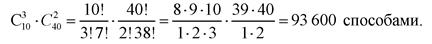
 ,
, — биномиальные коэффициенты,
— биномиальные коэффициенты,  — неотрицательное целое число.
— неотрицательное целое число.

 ≠0.
≠0.
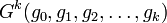 с нулевым элементом
с нулевым элементом  заданной на нём операцией
заданной на нём операцией  ,
,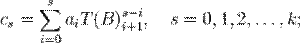

 , нулём —
, нулём —  Обратный элемент
Обратный элемент

 или множества комплексных чисел
или множества комплексных чисел 



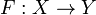 . Тогда его гра́фиком
. Тогда его гра́фиком  называется множество
называется множество ,
,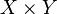 обозначает декартово произведение множеств
обозначает декартово произведение множеств  и
и  .
.  является кривая на двумерной плоскости.
является кривая на двумерной плоскости.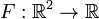 является поверхность в трёхмерном пространстве.
является поверхность в трёхмерном пространстве.
 .
.
 .
.
 .
. .
. .
. 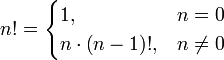
 (множество натуральных чисел с нулём).
(множество натуральных чисел с нулём).

 .
.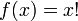

 .
.
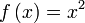 ;
; ;
; ;
;