
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 2. Ранг матрицы. ОпределителиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§3. Ранг матрицы Определение ранга матрицы Линейно зависимые строки Элементарные преобразования матриц Эквивалентные матрицы Алгоритм нахождения ранга матрицы с помощью элементарных преобразований §4. Определители первого, второго и третьего порядка Определитель первого порядка Определитель второго порядка Определитель третьего порядка Правило Саррюса §5. Вычисление определителей больших порядков Минор Алгебраическое дополнение Теорема Лапласа Определитель треугольной матрицы Приложение. Понятие определителя п -го порядка в общем виде.
§ 3. Ранг матрицы
Каждую матрицу характеризует некоторое число, имеющее важное значение при решении систем линейных уравнений. Это число называется рангом матрицы. Ранг матрицы равен числу ее линейно независимых строк (столбцов), чрез которые линейно выражаются все остальные ее строки (столбцы). Строки (столбцы) матрицы называются линейно зависимыми, если их соответствующие элементы пропорциональны. Иначе говоря, элементы одной из линейно зависимых строк равны элементам другой, умноженным на одно и то же число. Например, строки 1 и 2 матрицы А линейно зависимы, если
Пример. Найти ранг матрицы
Решение. Вторая строка получается из первой, если ее элементы умножить на –3, третья получается из первой, если ее элементы умножить на 0, а четвертая строка не может быть выражена через первую. Получается, матрица имеет две линейно независимые строки, т.к. первая и четвертая строки не пропорциональны, следовательно, ранг матрицы равен 2.
Ранг матрицы А обозначается rang A или r (A). Из определения ранга матрицы следует: 1. Ранг матрицы не превосходит наименьшего из ее размеров, т.е. для матрицы Аm × n 2. Ранг матрицы равен нулю, только если это нулевая матрица.
В общем случае определение ранга матрицы достаточно трудоемко. Для облегчения этой задачи используют преобразования, сохраняющие ранг матрицы, которые называются элементарными преобразованиями: 1) отбрасывание нулевой строки (столбца); 2) умножение всех элементов строки (столбца) на число, отличное от нуля; 3) изменение порядка строк (столбцов); 4) прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
5) транспонирование матрицы. Две матрицы называются эквивалентными, если одна получается из другой с помощью конечного числа элементарных преобразований. Эквивалентность матриц обозначается знаком «~» (эквивалентно). С помощью элементарных преобразований любую матрицу можно привести к треугольному виду, тогда вычисление ее ранга не представляет труда. Процесс вычисления ранга матрицы с помощью элементарных преобразований рассмотрим на примере.
Пример. Найти ранг матрицы А = Решение. Наша задача – привести матрицу к треугольному виду, т.е. с помощью элементарных преобразований добиться того, чтобы ниже главной диагонали в матрице были только нули. 1. Рассмотрим первую строку. Если элемент а 11 = 0, то при перестановке строк или столбцов добиваемся того, чтобы а 11 ¹ 0. В нашем примере поменяем местами, например, первую и вторую строки матрицы: А =
Теперь элемент а 11 ¹ 0. Умножая первую строку на подходящие числа и складывая с другими строками, добьемся того, чтобы все элементы первого столбца (кроме а 11) равнялись нулю.
2. Рассмотрим теперь вторую строку. Если элемент а 22 = 0, то при перестановке строк или столбцов добиваемся того, чтобы а 22 ¹ 0. Если элемент а 22 ¹ 0 (а у нас а 22 = –1 ¹ 0), то, умножая вторую строку на подходящие числа и складывая с другими строками, добьемся того, чтобы все элементы второго столбца (кроме а 22) равнялись нулю.
3. Если в процессе преобразований получаются строки (столбцы), целиком состоящие из нулей, то отбрасываем их. В нашем примере отбросим строки 3-ю и 4-ю:
Последняя матрица имеет ступенчатый вид и содержит две строки. Они линейно независимы, следовательно, ранг матрицы равен 2.
§ 4. Определители первого, второго и третьего порядка
Среди всего многообразия матриц отдельно выделяют квадратные. Этот тип матриц хорош тем, что: 1. Единичные матрицы – квадратные. 2. Можно умножать и складывать любые квадратные матрицы одного порядка, при этом получается матрица того же порядка. 3. Квадратные матрицы можно возводить в степень. Кроме того, только для квадратных матриц может быть вычислен определитель.
Определитель матрицы – это особое число, вычисляемое по некоторому правилу. Определитель матрицы А обозначается: - или прямыми скобками: - или заглавной греческой буквой «дельта»: Δ(A), - или символом «детерминант»: det (A).
Определителем матрицы первого порядка А = (а 11) или определителем первого порядка, называется число, равное элементу матрицы: Δ1 = Определителем матрицы второго порядка Δ2 = Пример:
Определителем матрицы третьего порядка Δ3 =
Определитель третьего порядка можно вычислить, пользуясь правилом Саррюса [3]. Правило Саррюса. К определителю третьего порядка справа подписывают два первых столбца и со знаком плюс (+) берут сумму произведений трех элементов, расположенных на главной диагонали определителя и на «прямых», параллельных главной диагонали, со знаком минус (–) берут сумму произведений элементов, расположенных на второй диагонали и на «прямых», параллельных ей.
Пример:
Легко заметить, что число слагаемых в определителе увеличивается с увеличением его порядка. Вообще в определителе п -го порядка число слагаемых равно 1·2·3·…· п = п!. Проверим: для Δ1 число слагаемых равно 1! = 1, для Δ2 число слагаемых равно 2! = 1·2 = 2, для Δ3 число слагаемых равно 3! = 1·2·3 = 6. Отсюда следует, что для определителя 4-го порядка число слагаемых равно 4! = 1·2·3·4 = 24, а значит вычисление такого определителя достаточно трудоемко, не говоря уже об определителях более высокого порядка. Учитывая это, вычисление определителей больших порядков стараются свести к вычислению определителей второго или третьего порядков.
§ 5. Вычисление определителей больших порядков
Введем ряд понятий. Пусть дана квадратная матрица А n -го порядка:
Минором M ij элемента a ij называется определитель (п – 1)-го порядка, полученной из матрицы А вычеркиванием i -oй строки и j -го столбца. Например, минором элемента а 12 матрицы третьего порядка будет:
Алгебраическим дополнением А ij элемента a ij называется его минор, взятый со знаком (−1) i + j: А ij = (−1) i + jM ij Иначе говоря, А ij = M ij, если i + j четное число, А ij = − M ij, если i + j нечетное число.
Пример. Найти алгебраические дополнения элементов второй строки матрицы
Решение.
С помощью алгебраических дополнений можно высчитывать определители больших порядков, на основании теоремы Лапласа.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения:
(
Пример. Вычислить определитель матрицы Решение.
Таким образом, определитель любого порядка можно свести к вычислению нескольких определителей меньшего порядка. Очевидно, что для разложения удобно выбирать строку или столбец, содержащую как можно больше нулей. Рассмотрим еще один пример. Пример. Вычислить определитель треугольной матрицы Решение.
Получили, что определитель треугольной матрицы равен произведению элементов ее главной диагонали. Этот важный вывод позволяет легко вычислить определитель любой треугольной матрицы. Это тем более полезно, что при необходимости всякий определитель можно свести к треугольному виду. При этом используются некоторые свойства определителей.
Приложение
Понятие определителя п -го порядка в общем виде.
Вообще можно дать строгое определение для определителя матрицы п -го порядка, но для этого необходимо ввести ряд понятий.
Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12...n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3! = 6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i > j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего. Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n -ой степени. Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ
обозначает подстановку, в которой 3 переходит в 4, 1 – в 2, 2 – в 1, 4 – в 3. Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n -ой степени может быть записана в виде
т.е. с натуральным расположением чисел в верхней строке. Пусть нам дана квадратная матрица порядка n
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
где индексы q 1, q 2,..., qn составляют некоторую перестановку из чисел Определителем n -го порядка называется алгебраическая сумма всех возможных произведений по n элементов матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
Линейная алгебра
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1759; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.126.43 (0.011 с.) |

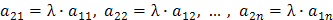 , где (λ – некоторое число).
, где (λ – некоторое число).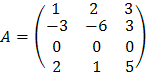
 .
.




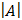 ,
, = а 11
= а 11 или определителем второго порядка, называется число, которое вычисляется по формуле:
или определителем второго порядка, называется число, которое вычисляется по формуле:

 или определителем третьего порядка, называется число, которое вычисляется по формуле:
или определителем третьего порядка, называется число, которое вычисляется по формуле:
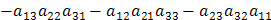

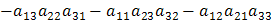
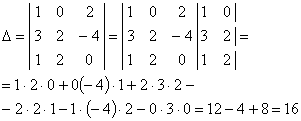
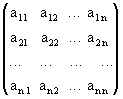





 – разложение по i-ой строке;
– разложение по i-ой строке; – разложение по j-му столбцу).
– разложение по j-му столбцу). разложением по первой строке.
разложением по первой строке.
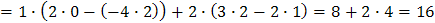




 ,
, ,
,


