
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство непрерывных функций на сегментеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Функция f(x) называется непрерывной на сегменте [а, b], если она непрерывна в интервале (а, b) и кроме того в точке а непрерывна справа, а в точке b слева. Теорема 1. Если функция f(x) непрерывна на сегменте [а, b], и на концах его принимает значения разных знаков, то между точками а и b найдется точка с такая, что f (c)=0 Это свойство имеет простой геометрический смысл, если непрерывная кривая переходит с одной стороны оси ox на другую, то она пересекает ось ox. Теорема 2. Если функция f(x) непрерывна на сегменте [а, b], то она ограничена на нем, т.е. существует такое положительное М, что Теорема 3. Если функция f(x) непрерывна на сегменте [a, b], то на этом сегменте найдутся точки x1 и x2 такие, что значения функции f(x1) и f(x2) будут соответственно наибольшим и наименьшим из всех значений функции f(x) на сегменте [a, b]. Определение производной Производной у' или f’(x) от данной функции y= f(x) называется предел отношения приращения функции к вызвавшему его приращению аргумента при условии, что приращение аргумента стремится к нулю: Непрерывность и дифференцируемость функции Согласно определению, производная от данной функции y= f(x) равна пределу отношения приращения функции к приращению аргумента, когда последнее стремится к нулю: Функция, имеющая в данной точке x0 производную, называется дифференцируемой в этой точке; функция, имеющая производную во всех точках некоторого промежутка (a,b) называется дифференцируемой в этом промежутке. Очевидно, что необходимым условием дифференцируемости функции в данной точке или в данном промежутке является ее непрерывность (соответственно в точке или в промежутке); в самом деле, предел в правой части может существовать лишь тогда, когда Δy - бесконечно малая одновременно с Δx, т. е. когда функция непрерывна. Правила дифференцирования Операция отыскания производной от данной функции называется дифференцированием этой функции. Установим ряд правил, которые избавят нас от необходимости вычислять производную исходя непосредственно из ее определения.Производная от аргумента х, Полагая y=x, находим Δy =Δx. Поэтому Дифференциал функции Таким образом, установлены следующие предложения, характеризующие свойства дифференциала и связь его с приращением функции.. Дифференциал функции равен произведению ее производной на дифференциал аргумента (независимого переменного). Разность между приращением функции и Δy ее дифференциалом dy есть величина бесконечно малая более высокого порядка, чем приращение аргумента Δx, а также (при y’≠0) более высокого порядка, чем приращение функции Δy и ее дифференциал dy (в самом деле, при y’≠0 и Δx→0, Δy есть бесконечно малая того же порядка малости, что и Δx, так как Дифференциал функции имеет простой геометрический смысл: значение дифференциала функции, при данном значении аргумента x и данном приращении, Δx равно приращению ординаты касательной,, проведенной в точке с абсциссой x графика этой функции, при переходе от точки касания (с абсциссой x) к соседней точке касательной с абсциссой x+ Δx.В самом деле, соответствующее приращение ординаты касательной на рис. 4.5 изображается катетом KN треугольника MKN, в котором вторым катетом служит отрезок МК= Производные высших порядков Если задана произвольная дифференцируемая функция Определение производной второго порядка Производную от производной данной функции, если она существует, называют производной второго порядка, или второй производной, от данной функции и обозначают символом В связи с этим производную Определение производной n –го порядка. Примеры В общем случае производной порядка n+1 от данной функции называется производной от производной Производная 1. Найти производную Находим, выполняя последовательные дифференцирования: 2. Найти производную Первую производную от, sin x равную cos x, можно записать в следующем виде: В силу этого Дифференциалы высших порядков Дифференциалом второго порядка (его обозначают символом Находим Таким образом, второй дифференциал функции равен произведению ее второй производной на квадрат дифференциала независимого переменного:d2y=y”·dx2 Правило Лопиталя. Раскрытием неопределенности в математическом анализе называют отыскание предела Теперь, опираясь на теорему Коши, выведем правило Бернулли — Лопиталя для раскрытия неопределенностей, использующее производные. Основными видами неопределенностей являются два: Остальные виды неопределенностей, как увидим дальше, приводятся к основным двум видам: 1 случай. Неопределенность вида Примем 2 случай. Неопределенность вида Правило Бернулли — Лопиталя не применимо, если не
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.179.30 (0.007 с.) |


 или
или  Производная от функции y= f(x) сама является функцией аргумента х.Для получения производной при определенном значении х0 аргумента х мы придаем значению х0 приращение Δx, что вызывает соответствующее приращение функции Δy= f(x+ Δx)- f(x), затем составляем отношение приращений
Производная от функции y= f(x) сама является функцией аргумента х.Для получения производной при определенном значении х0 аргумента х мы придаем значению х0 приращение Δx, что вызывает соответствующее приращение функции Δy= f(x+ Δx)- f(x), затем составляем отношение приращений  и вычисляем предел этого отношения, зависящего как х0, так и от Δx, при, Δx→0 сохраняя x0 неизменным. Следовательно, такой предел [обозначим его f’(x0) ]
и вычисляем предел этого отношения, зависящего как х0, так и от Δx, при, Δx→0 сохраняя x0 неизменным. Следовательно, такой предел [обозначим его f’(x0) ]
 Но этот предел существует не для всякой функции, а если и существует, то не обязательно при всех значениях ее аргумента, для которых функция определена.
Но этот предел существует не для всякой функции, а если и существует, то не обязательно при всех значениях ее аргумента, для которых функция определена. .А так как предел постоянной равен ей самой, тo y’=1. Итак, (x)’=1Производная постоянной.Докажем, что производная постоянной равна нулю. В самом деле, если y=c, то Δy=0; поэтому при всяком Δx≠0 имеем
.А так как предел постоянной равен ей самой, тo y’=1. Итак, (x)’=1Производная постоянной.Докажем, что производная постоянной равна нулю. В самом деле, если y=c, то Δy=0; поэтому при всяком Δx≠0 имеем  . Но тогда (так как предел постоянной равен ей самой)
. Но тогда (так как предел постоянной равен ей самой)  Итак,(c)’=0 Производная суммы Докажем, что производная суммы дифференцируемых функций равна сумме их производных. Убедимся в этом для суммы двух функций (для большего числа слагаемых доказательство аналогичное).Пусть y=u+v; но тогда Δy =Δu + Δv. Деля на Δx, имеем
Итак,(c)’=0 Производная суммы Докажем, что производная суммы дифференцируемых функций равна сумме их производных. Убедимся в этом для суммы двух функций (для большего числа слагаемых доказательство аналогичное).Пусть y=u+v; но тогда Δy =Δu + Δv. Деля на Δx, имеем  . Отсюда, переходя к пределу при, Δx→0 находим (так как предел суммы равен сумме пределов): или y’=u’+v’ Производная произведения Найдем производную произведения двух дифференцируемых функций. y=u·v. Когда аргумент xполучает приращение
. Отсюда, переходя к пределу при, Δx→0 находим (так как предел суммы равен сумме пределов): или y’=u’+v’ Производная произведения Найдем производную произведения двух дифференцируемых функций. y=u·v. Когда аргумент xполучает приращение  , то функции и, v и у получат соответственно приращения
, то функции и, v и у получат соответственно приращения  , Δv и Δy, причем y+Δy =(u+Δu)·(v+ Δv). Отсюда находим Δy: Δy =(u+Δu)·(v+ Δv)-u·v=v· Δu+ u· Δv+ Δu·Δv.
, Δv и Δy, причем y+Δy =(u+Δu)·(v+ Δv). Отсюда находим Δy: Δy =(u+Δu)·(v+ Δv)-u·v=v· Δu+ u· Δv+ Δu·Δv. dy также будет бесконечно малой того же порядка, поскольку dy=y’ ·Δy). В силу этого последнего свойства при y’≠0 приращение функции Δy и ее дифференциал dy будут при бесконечно малом равносильными бесконечно малыми:
dy также будет бесконечно малой того же порядка, поскольку dy=y’ ·Δy). В силу этого последнего свойства при y’≠0 приращение функции Δy и ее дифференциал dy будут при бесконечно малом равносильными бесконечно малыми: , причем
, причем  Но тогда KN = МК
Но тогда KN = МК  что и требовалось доказать.
что и требовалось доказать. , то ее производная
, то ее производная  , как известно, в свою очередь является функцией того же аргументa x. Поэтому можно ставить вопрос об отыскании производной от этой функции.
, как известно, в свою очередь является функцией того же аргументa x. Поэтому можно ставить вопрос об отыскании производной от этой функции.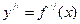 . Таким образом
. Таким образом 
 порядка этой функции:
порядка этой функции: .Очевидно, что в силу принятого нами определения производных высших порядков (если они существуют у данной функции), будет справедливо такое утверждение:
.Очевидно, что в силу принятого нами определения производных высших порядков (если они существуют у данной функции), будет справедливо такое утверждение: порядка от n-й производных высших порядков (если они существуют у данной функции), будет равна производной
порядка от n-й производных высших порядков (если они существуют у данной функции), будет равна производной  порядка от этой функции (
порядка от этой функции (  - целые положительные числа):
- целые положительные числа): 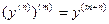 .Рассмотрим несколько примеров отыскания производных высших порядков.
.Рассмотрим несколько примеров отыскания производных высших порядков. .
. .
.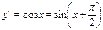 отсюда следует, что операция дифференцирования функции y=sin xпо x формально сводится к прибавлению
отсюда следует, что операция дифференцирования функции y=sin xпо x формально сводится к прибавлению  к аргументу синуса.
к аргументу синуса. ; поэтому
; поэтому  .
. ) от функции
) от функции  называют дифференциал ее дифференциала:
называют дифференциал ее дифференциала:  Найдем его выражение. Имеем
Найдем его выражение. Имеем  , причем
, причем  — произвольное приращение аргумента
— произвольное приращение аргумента  , которое от аргумента
, которое от аргумента 
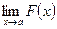 , когда функция
, когда функция  непрерывна вблизи точки
непрерывна вблизи точки  , но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения
, но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения 
 и
и  .
. и
и  (при
(при  ).
). ; тогда функции
; тогда функции  и
и  будут непрерывными в точке
будут непрерывными в точке  . Но отсюда еще не следует, что не существует предел отношения самих функций, т. е.
. Но отсюда еще не следует, что не существует предел отношения самих функций, т. е.  . Последний может и существовать. Но он не может только быть в этом случае найден по правилу Бернулли—Лопиталя.
. Последний может и существовать. Но он не может только быть в этом случае найден по правилу Бернулли—Лопиталя.


