
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое распределение выборки. Полигон и гистограмма.Содержание книги
Поиск на нашем сайте
Статистическим распределением выборки. Статистическое распределение записывается в виде таблицы: 1 строка – варианты; 2 строка – частоты. n – объем выборки(частота).Иногда вместо частот используют относительную частоту:Wi = ni / n; ΣWi = 1 Разность между наибольшим и наименьшим элементами выборки называется размахом выборки, т.е. R = xmax-xmin При большом объеме выборки ее элементы объединяются в группы. В процессе группированного ряда подсчитываются также накопленные частоты. ñi* - частота i-интервала равна сумме частот: ñ3* = ñ1+*ñ2*+ñ3* Ŵi*- накопленная относительная частота. Полигоном частот называется ломаная линия, вершинами которой служат точки с координатами (хi;ni), i=1…k.Для группировки выборки строят гистограмму частот, т.е. ступенчатую фигуру, состоящую из прямоугольников,площадь прямоугольника равна частоте ñi*.Площадь гистограммы равна объему выборки. Высота прямоугольников равна ñ*i / n. 81. Множества, основные определения и операции над ними. Одним из основополагающих понятий математического анализа являются множества. Множество - совокупность элементов, объектов, отнесенных в единую группу по нейким признакам. Примеры множеств: N - множество натуральных чисел. Z0 - множество чисел целых неотрицательных Z - множество целых чисел. R - множество действительных чисел. Q - множество рациональных чисел Множество B является подмножеством множества A, если каждый элемент множества B является элементом множества A. Символически это обозначают так
1) Объединение множеств(сумма) Результатом объединения множеств A и B будет являться множество C, состоящее из элементов,каждый из которых принадлежит хотя бы одному из этих множеств.
Операция обладает обычными свойствами: 1) АИВ= ВИА;
2) Пересечение множеств(произведение)
3) Разность множеств
Операция разность множеств обозначается следующим образом: С=А\В 4) Дополнение множества Дополнением множества A до множества B будет являться множество C такое, что любой элемент множества C является элементом множества B, и не является элементом множества A. Дополнение множества: Если предположим, что множество является подмножеством некоторого универсального множества, тогда определяется операция дополнения. 82. Отношения на множествах. Подмножество R Пример: отношения на натуральных числах N: 1) отношение 2) Отношение «иметь общий делитель, отличный от единицы» выполняется для пар (6, 9), (4, 2), (2,4), но не для (7, 9), (9,7). 3) Отношение «быть делителем», т. е. аRb (а делитель b) выполняется для пар (2, 4), (4, 4), но не для (4, 2), (7, 9). Отношения на конечных множествах задаются обычно списком или матрицей. Матрица бинарного отношения на множестве М={а1,…,аm} – это квадратная матрица С порядка m, в которой элемент сij i – ой строки и j-ого столбца определяется: Например, отношение 2) «иметь общий делитель Свойства отношений Отношение R называется рефлексивным, если для любого a Отношение R называется симметричным, если для пары (a,b) Отношение R антисимметрично, если при хRy и yRx следует х=у. Пример: отношение Отношение называется отношением эквивалентности (эквивалентно), если оно рефлексно, симметрично и транзитивно. Например, а) равные треугольники (их называют конгруэнтными) – могут быть переведены друг в друга (наложены). Они имеют отношение эквивалентности. б) отношение «иметь один и тот же остаток от деления» на 7 являются эквивалентностью на N (множество натуральных чисел). Это отношение выполняется например, для пар (11, 46), (14, 70) и т. д. Отношение называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично, и транзитивно. Отношение строгого порядка – если оно антирефлексно, антисимметрично и транзитивно. Оба эти отношения называют отношениями порядка. Отношения Отношения подчиненности администрации предприятия – отношение строго порядка: ген. директор – гл. инженер – начальник цеха и т. д. 83. Основные определения алгебры логики. Всякое утверждение, о котором можно сказать, что оно истинно или ложно, в логике называется высказыванием. Именно это свойство высказываний (быть истинными или ложными) представляет интерес для логики. Истинность либо ложность высказывания определяется отношением содержания утверждения к действительному положению вещей. При изучении высказываний предполагается, что выполняются следующие законы (традиционной) аристотелевской логики: закон исключенного третьего - каждое рассматриваемое высказывание либо истинно, либо ложно; закон противоречия - никакое высказывание не является одновременно истинным и ложным. Эти предположения, очевидно, абсолютизируют свойства реальности и в действительности далеко не всегда могут считаться выполненными (например, высказывания "квант света есть волна" и "квант света есть частица" не соответствуют требованиям этих законов). Основная задача алгебры высказываний - изучение логических операций над высказываниями, при которых истинность результирующих высказываний определяется только лишь значениями истинности исходных высказываний. С этой целью высказывания делятся на элементарные и составные. Высказывание считается элементарным, если в нем нельзя выделить более простое высказывание, в противном случае высказывание считается составным. Например, высказывания "не всякий студент - отличник" и "это пошел дождь или кто-то включил душ" являются составными, поскольку в них можно выделить более простое высказывание "всякий студент - отличник", а также элементарные высказывания: "студент - отличник", "это пошел дождь", "кто-то включил душ". Элементарным высказываниям в алгебре логики ставятся в соответствие переменные, принимающие значения "истина" или "ложь" и называемые по этой причине логическими переменными или пропозициональными переменными (от латинского слова propositio - высказывание). Вместо слов "истина" и "ложь" в литературе используются различные символы. Мы будем придерживаться принятых в отечественной литературе обозначений: символом 1 обозначается "истина", а символом 0 - "ложь". Обозначение простейших исходных высказываний с помощью переменных, принимающих значения "истина" или "ложь", позволяет рассматривать составные высказывания как истинностные функции от этих переменных, а слова, связывающие элементарные высказывания между собой, - как логические операции (связки). 84. Основные определения ткории графов Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В этих задачах несущественно, соединены ли точки конфигурации отрезками прямых или криволинейными дугами, какова длина линий и другие геометрические характеристики конфигурации. Важно лишь то, что каждая линия соединяет какие-либо две из заданных точек. Определение графа: Совокупность двух множеств V (точек) и Е (линий), между элементами которых определено отношение инцидентности, причем каждый элемент e E инцидентен ровно двум элементам v V.Элементы множества V называются вершинами графа G, элементы множества Е – его ребрами. Вершины и ребра графа G называют еще его элементами и вместо v V, e E пишут соответственно v G, e G. Направленные ребра часто называют дугами, а содержащий их граф – ориентированным (граф, определенный ранее, называется неориентированным). Первая по порядку вершина, инцидентная ребру ориентированного графа, называется его началом, вторая – его концом. Говорят еще, что ребро ориентированного графа выходит из начала и входит в конец. Пути и циклы в графе. Путем в графе (или маршрутом в орграфе) называется чередующаяся последовательность вершин и ребер (или дуг - в орграфе) вида v0, (v0,v1), v1,..., (vn-1,vn), vn. Число n называется длиной пути. Путь без повторяющихся ребер называется цепью, без повторяющихся вершин - простой цепью. Путь может быть замкнутым (v0=vn). Замкнутый путь без повторяющихся ребер называется циклом (или контуром в орграфе); без повторяющихся вершин (кроме первой и последней) - простым циклом. Утверждение 1. Если в графе существует путь, ведущий из вершины v0 в vn, то существует и простая цепь между этими вершинами. Доказательство. Такую простую цепь можно построить, "выкинув" из пути все циклы. Граф называется связным, если существует путь между любыми двумя его вершинами, и несвязным - в противном случае. Несвязный граф состоит из нескольких связных компонент (связных подграфов). Для орграфов понятие связности является более сложным: различают сильную связность, одностороннюю связность и слабую связность. Орграф называется сильно связным, если для любых двух его вершин v и u существует как маршрут из v в u (v->u), так и из u в v (u->v). Орграф называется односторонне связным, если для любых двух его вершин u и v существует, по крайней мере, один из маршрутов v->u или u->v. Наконец, орграф называется слабо связным, если связан неориентированный граф, получаемый из этого орграфа путем снятия ориентации с дуг. Очевидно, что любой сильно связный граф является односторонне связным, а односторонне связный - слабо связным, но не наоборот. 86.Основные определения теории алгоритмов. Алгоритм - это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения (после конечного числа шагов) искомого результата. Понятие алгоритма является одним из основных понятий современной математики и является объектом исследования специального раздела математики - теории алгоритмов. Алгоритм Евклида 1. Поместить в участок памяти с именем x число m; перейти к выполнению пункта 2. 2. Поместить в участок памяти с именем y число n; перейти к выполнению пункта 3. З. Если выполняется условие, то перейти к выполнению пункта 5, иначе перейти к выполнению пункта 4. 4. Поместить в участок памяти с именем НОД значение из блока памяти x; перейти к выполнению пункта 8. 5. Если выполняется условие x > y, то перейти к выполнению пункта 6, иначе перейти к выполнению пункта 7; 6. Поместить в участок памяти с именем x значение выражения x - y; перейти к выполнению пункта 3. 7. Поместить в участок памяти с именем y значение выражения y - x; перейти к выполнению пункта 3. 8. Закончить работу.
1. Нормальное уравнение плоскости в векторной и координатной формах (вывод).
По условию, Уравнение (4.36) называется векторным уравнением плоскости. Одновременно уравнение (4.36) называется нормальным уравнением плоскости. Пусть теперь единичный вектор При этом уравнение (4.36) примет вид: Уравнение (4.36) называется нормальным (нормированным) уравнением плоскости в координатной форме. Замечание: как и в случае нормального уравнения прямой, в рассматриваемом случае уравнение (4.37) можно получить, используя теорию проекций.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.80 (0.013 с.) |

 А В (А включено в В)
А В (А включено в В)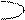
 Множества А и В равны или совпадают, и пишут А=В, если А В и В А, т.е. множества, состоящие из одних и тех же элементов, называют равными.
Множества А и В равны или совпадают, и пишут А=В, если А В и В А, т.е. множества, состоящие из одних и тех же элементов, называют равными.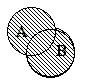 Операции над множествами
Операции над множествами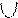
 2) АИ(ВИС)=(АИВ) ИС.
2) АИ(ВИС)=(АИВ) ИС.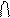
 Результатом разности множеств A и B будет являться множество C такое, что любой элемент множества C является элементом множества A, и не является элементом множества B.
Результатом разности множеств A и B будет являться множество C такое, что любой элемент множества C является элементом множества A, и не является элементом множества B. Mn называется n-местным отношением на множестве М. Одноместное отношение – это просто подмножество М. Такие одноместные отношения называют признаками: а обладает признаком R, если а
Mn называется n-местным отношением на множестве М. Одноместное отношение – это просто подмножество М. Такие одноместные отношения называют признаками: а обладает признаком R, если а  R и R
R и R  выполняется для пар (7, 9) и (7, 7),но не для (9, 7).
выполняется для пар (7, 9) и (7, 7),но не для (9, 7).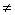 1» для М={1, 2, 3, 4, 5, 6}
1» для М={1, 2, 3, 4, 5, 6} M имеет место аRa. Наоборот антирефлексным, если ни для какого a
M имеет место аRa. Наоборот антирефлексным, если ни для какого a  - отношения нестрогого порядка. Отношения < и > - отношения строгого порядка. Оба они упорядочивают множества N и R.
- отношения нестрогого порядка. Отношения < и > - отношения строгого порядка. Оба они упорядочивают множества N и R. Положение плоскости в трехмерном пространстве будет вполне определено, если известно ее расстояние P от начала координат O, т.е. длина перпендикуляра ON, опущенного из точки O на плоскость, и единичный вектор
Положение плоскости в трехмерном пространстве будет вполне определено, если известно ее расстояние P от начала координат O, т.е. длина перпендикуляра ON, опущенного из точки O на плоскость, и единичный вектор  , перпендикулярный к плоскости.
, перпендикулярный к плоскости.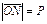 . Для любой точки M(x,y,z), лежащей на плоскости, имеем (см рис)
. Для любой точки M(x,y,z), лежащей на плоскости, имеем (см рис)  пр
пр 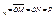 . С другой стороны, по определению скалярного произведения двух векторов имеем:
. С другой стороны, по определению скалярного произведения двух векторов имеем: или
или  (4.36)
(4.36)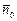 образует с осями координат соответственно углы α, β, γ. Тогда
образует с осями координат соответственно углы α, β, γ. Тогда  . Далее, вектор
. Далее, вектор 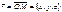 . Тогда получим скалярное произведение векторов:
. Тогда получим скалярное произведение векторов:
 (4.37)
(4.37)


