
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальное (безвихревое) полеСодержание книги
Поиск на нашем сайте
Если во всех точках поля ротор равен нулю, то поле называется безвихревым. Если мы возьмем замкнутую векторную линию и рассмотрим циркуляцию вдоль этой замкнутой линии, то Это значит, что поток вектора 57. Дифференциальные уравнения 1 порядка, задача Коши. Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида F (x, y, y ')=0, где F — известная функция трех переменных, определенная в области G из R 3, x — независимая переменная из интервала (a, b), y (x) — неизвестная функция, y '(x) — ее производная. Обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения вида y '= f (x, y) называют уравнениями в нормальной форме. Задача Коши. З аключается в нахождении решения u (x, t); х = (x1,..., xn) дифференциального уравнения вида: удовлетворяющего т. н. начальным условиям. где G 0 — носитель начальных данных — область гиперплоскости t = to пространства переменных x1,..., xn. Когда F и fk, k = 0, ..., m — 1, являются аналитическими функциями своих аргументов, задача Коши (1), (2) в некоторой области G пространства переменных t, х, содержащей G0, всегда имеет и притом единственное решение. Однако это решение может оказаться неустойчивым (т. е. малое изменение начальных данных может вызвать сильное изменение решения), например в том случае, когда уравнение (1) принадлежит эллиптическому типу. Линейные дифференциальные уравнения первого порядка Линейным уравнением первого порядка называют уравнения вида
где Существуют несколько методов решения этого уравнения. Метод вариации произвольной постоянной (метод Лагранжа). Сначала решаем однородное уравнение
методом разделения переменных
Тогда все решения уравнения (1) определяются формулой
Метод Бернулли. Решение уравнения (1) ищем в виде
где
Однородные ДУ первого порядка Определение 1. Функция n -го измерения относительно переменных x и y, если при любом λ справедливо тождество Например, функция Определение 2. Уравнение первого порядка Эти частные решения имеют вид которые называются особыми решениями.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.111.109 (0.006 с.) |

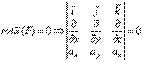 . Потенциал поля,Тогда выражение axdx+aydy+azdz является полным дифференциалом некоторой функции u(x,y,z), т.е
. Потенциал поля,Тогда выражение axdx+aydy+azdz является полным дифференциалом некоторой функции u(x,y,z), т.е Тогда
Тогда  Функция u называется потенциалом векторного поля, а градиент ее направлен по касательной к векторной линии.Справедливо и обратное утверждение. Поле градиента любой функции u(x,y,z)является потенциальным, а сама функция u - его потенциалом.В потенциальном поле циркуляция по любому замкнутому контуру равна нулю.Потенциальное поле вполне определяется его потенциалом.
Функция u называется потенциалом векторного поля, а градиент ее направлен по касательной к векторной линии.Справедливо и обратное утверждение. Поле градиента любой функции u(x,y,z)является потенциальным, а сама функция u - его потенциалом.В потенциальном поле циркуляция по любому замкнутому контуру равна нулю.Потенциальное поле вполне определяется его потенциалом.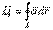 где
где 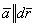 Тогда,
Тогда, 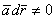 Итак, циркуляция вдоль замкнутой векторной линии не равна нулю. Следовательно, в безвихревом поле
Итак, циркуляция вдоль замкнутой векторной линии не равна нулю. Следовательно, в безвихревом поле 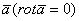 не могут существовать замкнутые векторные линии при условии, что области ими ограниченные целиком лежат в векторном поле.Трубчатое (соленоидальное) поле Векторное поле, для всех точек которого дивергенция равна нулю, называется трубчатым или соленоидальным. Возьмем в этом поле какую-нибудь площадку S1 и проведем через каждую точку ее границы векторные линии. Эти линии ограничивают часть пространства, называемую векторной трубкой По условию
не могут существовать замкнутые векторные линии при условии, что области ими ограниченные целиком лежат в векторном поле.Трубчатое (соленоидальное) поле Векторное поле, для всех точек которого дивергенция равна нулю, называется трубчатым или соленоидальным. Возьмем в этом поле какую-нибудь площадку S1 и проведем через каждую точку ее границы векторные линии. Эти линии ограничивают часть пространства, называемую векторной трубкой По условию 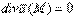 . Тогда по формуле Остроградского-Гаусса имеем:
. Тогда по формуле Остроградского-Гаусса имеем: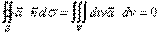 где V - тело, ограниченное векторной трубкой.
где V - тело, ограниченное векторной трубкой.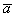 в направлении векторных линий соленоидального поля один и тот же, т.е. через каждое сечение протекает одно и то же количество жидкости, поэтому векторные линии не могут начинаться или обрываться внутри области G, а векторные трубки такого поля либо замкнуты, либо выходят на границы области, где определен вектор
в направлении векторных линий соленоидального поля один и тот же, т.е. через каждое сечение протекает одно и то же количество жидкости, поэтому векторные линии не могут начинаться или обрываться внутри области G, а векторные трубки такого поля либо замкнуты, либо выходят на границы области, где определен вектор 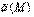 .
.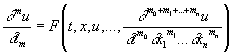 , (1)
, (1) m 0 < m, m > 0,
m 0 < m, m > 0, , t = t 0, x Î G 0, k = 0, …, m-1, (2)
, t = t 0, x Î G 0, k = 0, …, m-1, (2) (1)
(1) - заданные функции независимого переменного x, определенные на некотором интервале
- заданные функции независимого переменного x, определенные на некотором интервале  .
.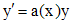
 или
или 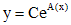 , где
, где 
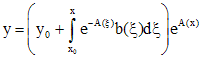
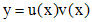 . Подставляем данное выражение в (1),решением которого является функция
. Подставляем данное выражение в (1),решением которого является функция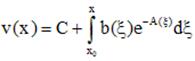 ,
, - произвольная постоянная. Перемножая
- произвольная постоянная. Перемножая 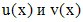 , получим (3).
, получим (3).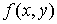 называется однородной функцией
называется однородной функцией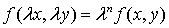 .
.
 называется однородным относительно x и y, если функция
называется однородным относительно x и y, если функция  ,
,


