
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения прямой на плоскости: С угловым коэффициентом; через две точки; в отрезках, общее уравнениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение прямой с угловым коэффициентом
Уравнение прямой, проходящей через две точки
Уравнение прямой в отрезках (рис 4.3)
Общее уравнение прямой на плоскости Рассмотрим общее уравнение первой степени относительно x и y: Ax+By+C=0 (4.10), где A, B, C – произвольные числа. Уравнение (4.10) называется общим уравнением прямой. 10. Уравнения плоскости: в векторной, координатной формах.
Уравнение (4.45) есть векторное уравнение плоскости, проходящей через точку M0. Но
Мы пришли к уравнению плоскости, проходящей через данную точку, в координатной форме. 11. Уравнение прямой в пространстве.
Уравнения (4.57) определяют общее уравнение прямой в пространстве, если плоскости, определяемые этими уравнениями, различны и не параллельны, где n1=(A1,B1,C1), n2=(A2,B2,C2). В декартовой системе прямоугольных координат уравнение любой плоскости приводится к виду Ах+Ву+Сz+D=0, где A,B,C,D - заданные числа, причем А2+В2+С2>0. 12. Расстояние от точки до плоскости. Если уравнение плоскости задано в общем виде Ax + By + Cz + D = 0, то, чтобы найти расстояние от данной точки M0(x0,y0,z0),то расстояние от точки до плоскости находится по формуле:
13. Условия параллельности и перпендикулярности векторов. Условием параллельности (коллинеарности) векторов является векторное произведение, равное нулю. Условием перпендикулярности (ортогональности) векторов является скалярное произведение, равное нулю. 14. Канонические уравнения кривых второго порядка: формулы, определения, чертеж. Каноническое уравнение окружности Определение. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки называемой центром. Рассмотрим на кривой любую произвольную точку M (x, y) и обозначим C 0(x 0, y 0) через центр окружности. Тогда CM = Возведя обе части в квадрат, получим:
Уравнение (5.2.) называется каноническим уравнением окружности. Каноническое уравнение эллипса Определение. Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2 a. Для вывода канонического уравнения эллипса выберем начало O декартовой системы координат в середине отрезка F 1 F 2. Обозначим через 2 C расстояние F 1 F 2 = 2 C и F 1 (- С, 0), F 2 (С, 0). Рассмотрим любую произвольную точку M (x, y) на эллипсе. Тогда по определению F 1 М + F 2 М = 2 a, где F 1М=
Определение. Гиперболой называется геометрическое место точек плоскости, для которых разность расстояний до двух точек, называемых фокусами, есть величина постоянная, равная 2 а. Чтобы составить уравнение гиперболы, возьмем за ось ОХ прямую, проходящую через точки F 1 (С, 0) и F 2 (- С, 0). Обозначим через 2 С расстояние между F 1 и F 2, т.е. F 1 F 2 = 2 С. Через середину отрезка F 1 F 2 проведем ось OY. Рассмотрим любую произвольную точку M (x, y) на гиперболе. Тогда по определению F 1 М - F 2 М = ± 2 a. Тогда Определение параболы и вывод её канонического уравнения Определение. Параболой называется геометрическое место точек плоскости, равностоящих от одной точки, называемой фокусом, и данной прямой, называемой директрисой. Чтобы составить уравнение параболы, примем за ось Ox прямую, проходящую через фокус F перпендикулярно к директрисе. Будем считать, что начало координат O совпадает с серединой отрезка AF (рисунок 5.5), длина которого равна параметру P. Фокус F имеет координаты F(P/2; 0). Рассмотрим на параболе произвольную точку M(x,y). Тогда по определению FM = MN, где N (-P/2;y). Уравнение (5.19) называется каноническим уравнением параболы.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.224 (0.007 с.) |

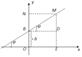 Определение. Тангенс угла наклона прямой к оси OX называется угловым коэффициентом прямой и обозначают
Определение. Тангенс угла наклона прямой к оси OX называется угловым коэффициентом прямой и обозначают 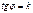 . y=kx+b
. y=kx+b
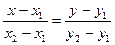 – каноническое уравнение прямой на плоскости.
– каноническое уравнение прямой на плоскости.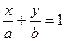
 Рассмотрим на плоскости произвольную точку M(x,y, z). Тогда (ри сунок 4.12)
Рассмотрим на плоскости произвольную точку M(x,y, z). Тогда (ри сунок 4.12) 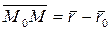 . Так как вектор
. Так как вектор 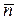 перпендикулярен плоскости, то
перпендикулярен плоскости, то  . Следовательно,
. Следовательно, 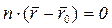 (4.45)
(4.45)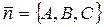 , а
, а 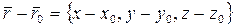 . Тогда скалярное произведение векторов, т.е. левая часть (4.45), будет:
. Тогда скалярное произведение векторов, т.е. левая часть (4.45), будет: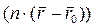 = A (x – x0) + B (y – y0) + C (z – z0) = 0 (4.44)
= A (x – x0) + B (y – y0) + C (z – z0) = 0 (4.44)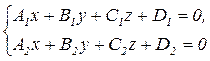 (4.57)
(4.57)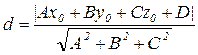 .
.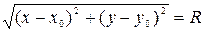 — радиус окружности.
— радиус окружности.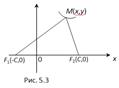
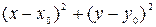 = R 2 (5.2)
= R 2 (5.2)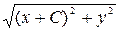 и F 2М=
и F 2М= 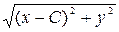 . Тогда
. Тогда 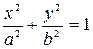 это и называется каноническим уравнением эллипса.
это и называется каноническим уравнением эллипса. Каноническое уравнение гиперболы.
Каноническое уравнение гиперболы.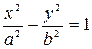 это уравнение называется каноническим уравнением гиперболы.
это уравнение называется каноническим уравнением гиперболы.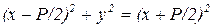 или
или 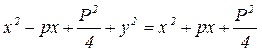 , откуда
, откуда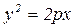 (5.19)
(5.19)


