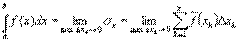Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование выражений, содержащих тригонометрические функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В случае, когда подынтегральная функция представляет собой целую степень тригонометрической функции или произведение целых степеней применяют приемы, основанные на использовании формул тригонометрии и на применении общих методов интегрирования. 1) Интеграл от нечетной положительной степени синуса и косинуса. 2) Интеграл от четной положительной степени синуса и косинуса. 3) Интеграл от произведения целых положительных степеней синуса я косинуса. Приемы интегрирования целой положительной степени синуса и косинуса, изложенные в пунктах 1) и 2), достаточны для интегрирования произведений таких степеней, как это следует из приводимых ниже примеров. 4) Интеграл от нечетной положительной степени секанса и косеканса. Значит Получена рекуррентная формула. Последовательно применяя эту формулу, получим выражение наконец, 5) Интеграл от четной положительной степени секанса и косеканса. Развернув (k — 1)-ю степень двучлена l + tg2x, придем к сумме табличных интегралов. 6) Интеграл от целой положительной степени тангенса и котангенса. Получена рекуррентная формула Универсальная тригонометрическая подстановка. Функция с переменными sin x и cos x, над которыми выполняются рациональные действия(сложение, вычитание, сложение, деление) принято обозначать R(sin x; cos x),где R- знак рациональной функции. Вычисление неопределенных интегралов типа ∫R(sin x; cos x) dx сводится к вычислению интегралов от рациональной функции подстановкой tg Правила подстановки: Если функция R(sin x; cos x) нечетна относительно sin x, т.е. R(-sin x; cos x) = -R(sin x; cos x), то подстановка cos x= t рационализирует интеграл; Если функция R(sin x; cos x)нечетна относительно cos x, т.е. R(sin x; -cos x) = -R(sin x; cos x), то делается подстановка sin x= t; Если функция R(sin x; cos x) четна относительно sin x и cos x R(-sin x; -cos x) = R(sin x; cos x), тоинтеграл рационализируется подстановкой tg x = t. Такая же подстановка применяется, если интеграл имеет вид ∫R(tg x) dx. Интегрирование иррациональностей. 1. Вычисление интегралов вида: где R —символ рациональной зависимости. Подинтетральная функция -рациональная функция от аргумента х и нескольких дробных степеней одной и той же дробно-линейной функции этого аргумента х. Применяется подстановка: где В — общее наименьшее кратное чисел Эта подстановка приводит все подинтегральное выражение к рациональному виду. Из равенства, х выражается рационально через t; обозначается он так: где 2. Вычисление интегралов от рациональной функции аргумента х и квадратного радикала из квадратного двучлена: Вычисление таких интегралов производится с помощью соответствующей тригонометрических подстановок: 1) 2) 3) Во всех трех случаях подрадикальное выражение превращается в точный квадрат, радикал исчезает, а интеграл получает вид Определенный интеграл как предел интегральных сумм. Определенным интегралом В символе определенного интеграла а и b называются нижним и верхним пределами интегрирования, отрезок [а, b] - отрезком интегрирования, f(x) называется под интегральной функцией, a f(x)dx - подинтегральным выражением; х называется переменной интегрирования.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 537; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.214 (0.007 с.) |

 ,
, ..
..
 получим конечное число интегралов от четных и от нечетных степеней cos 2x. В случае четной степени, снова воспользуемся формулой тригонометрии
получим конечное число интегралов от четных и от нечетных степеней cos 2x. В случае четной степени, снова воспользуемся формулой тригонометрии  а в случае нечетной степени применим прием 1). Через конечное число шагов придем к сумме табличных интегралов.
а в случае нечетной степени применим прием 1). Через конечное число шагов придем к сумме табличных интегралов.

 через
через 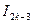 ,
,  и т. д.;
и т. д.; — через
— через  . Используя теперь полученные нами выражения в обратном порядке, найдем
. Используя теперь полученные нами выражения в обратном порядке, найдем  .
. ..
..
 .
. = t,которая называется универсальной.
= t,которая называется универсальной. ,
,
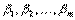 .
. . Тогда
. Тогда 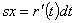 , где r'(t) есть рациональная функция t, как производная от рациональной функции r(t).
, где r'(t) есть рациональная функция t, как производная от рациональной функции r(t). ,
, — целое число, т.к. В делится без остатка на каждое из чисел
— целое число, т.к. В делится без остатка на каждое из чисел 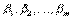 Имеем:
Имеем: ,где
,где  есть рациональная функция аргумента t.
есть рациональная функция аргумента t.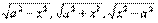 .
. , в случае интеграла
, в случае интеграла  ;
; , в случае интеграла
, в случае интеграла 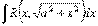
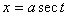 , в случае интеграла
, в случае интеграла  ..
..
 от функции f(x) на отрезке [а, b] называется предел, к которому стремится интегральная сумма, составленная для этой функции на этом отрезке, когда наибольшая длина элементарных отрезков, на которые разбит отрезок [а, b], стремится к нулю:
от функции f(x) на отрезке [а, b] называется предел, к которому стремится интегральная сумма, составленная для этой функции на этом отрезке, когда наибольшая длина элементарных отрезков, на которые разбит отрезок [а, b], стремится к нулю: