
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные методы интегрирования.Содержание книги
Поиск на нашем сайте Непосредственное интегрирование. Непосредственное интегрирование предполагает использование свойств неопределенного интеграла, таблицы интегралов и различных формул из элементарной математики.
Пример. Решение. Воспользуемся формулой сокращенного умножения (квадрат суммы), свойствами степеней, свойствами 3-4 и формулой 1 таблицы интегралов:
Замена переменной. Пусть требуется найти интеграл с непрерывной подынтегральной функцией Сделаем замену переменных, положив 1) 2) Тогда После интегрирования возвращаются к старой переменной обратной подстановкой. Пример. Решение.
Пример. Решение.
Интегрирование по частям. Интегрированием по частям называется нахождение интеграла по формуле:
где Применяется формула в следующих случаях: 1) Подынтегральная функция является произведением многочлена на показательную или тригонометрическую функцию. Это интегралы вида: В этом случае в качестве Пример. Решение. Подынтегральная функция есть произведение многочлена на тригонометрическую функцию (1 случай). Поэтому в качестве
2) Подынтегральная функция является произведением многочлена на логарифмическую или обратную тригонометрическую функцию. Это интегралы вида: В качестве Пример. Решение. Подынтегральная функция есть логарифмическая функция (2 случай). Поэтому в качестве
Интегрирование рациональных дробей.
Пример. Решение. Сначала разложим дробь на простейшие:
Решая систему, получим: Тогда исходный интеграл примет вид:
Пример. Решение. Так как дробь является неправильной, то сначала выделим целую часть. В результате получим:
Теперь вычислим интеграл:
Пример. Решение. Подынтегральная дробь является правильной, так как степень многочлена в числителе меньше, чем в знаменателе. Разложим дробь на простейшие:
Решая систему, получим: Тогда исходный интеграл примет вид:
Интегрирование тригонометрических выражений. Пример. Решение.
б) Оба числа m, n - четные неотрицательные. Применим формулы:
Пример. Решение.
|
||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

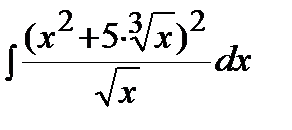 .
.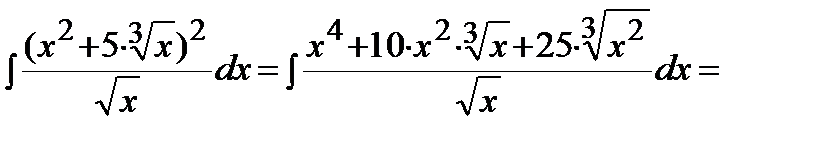
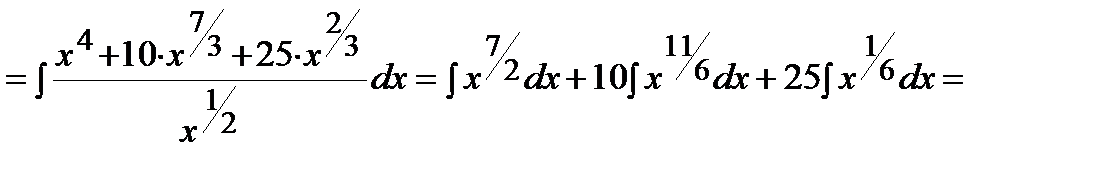
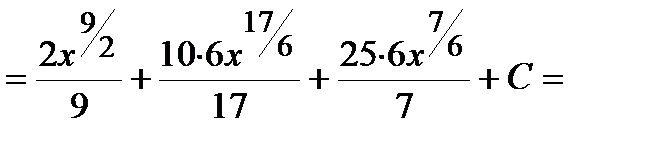
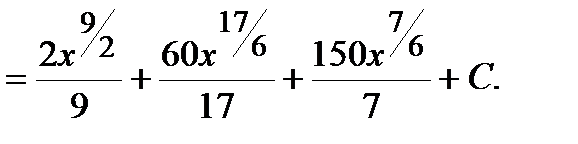
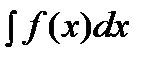 .
.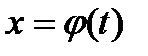 , где функция
, где функция 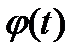 удовлетворяет следующим двум условиям:
удовлетворяет следующим двум условиям: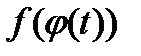 - непрерывная функция;
- непрерывная функция;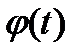 - непрерывно дифференцируемая функция, имеющая обратную функцию.
- непрерывно дифференцируемая функция, имеющая обратную функцию.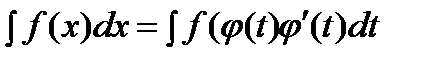 .
.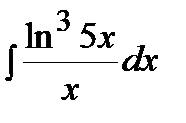 .
. .
. .
.
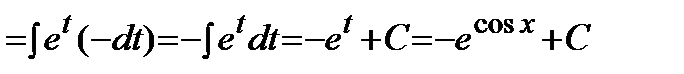 .
.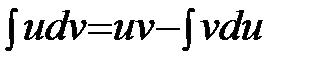 ,
,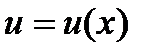
 и
и  — непрерывно дифференцируемые функции от
— непрерывно дифференцируемые функции от  . С помощью этой формулы нахождение интеграла
. С помощью этой формулы нахождение интеграла  сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 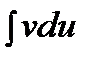 . Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.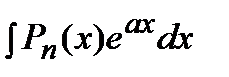 ,
, 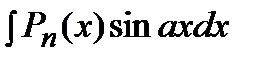 ,
, 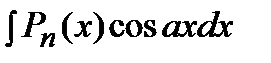 .
.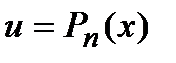 .
.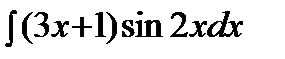 .
.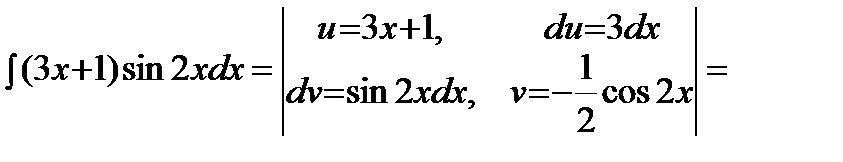
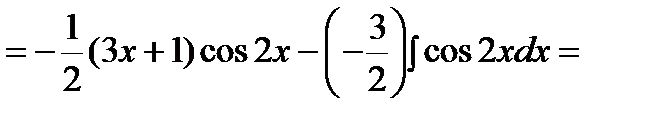
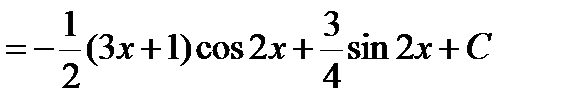 .
. ,
,  ,
,  ,
, 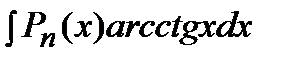 ,
, 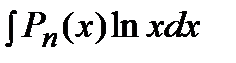 .
.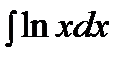 .
.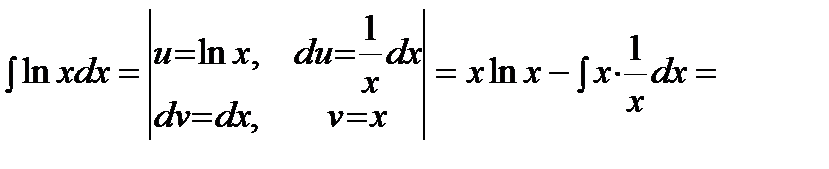
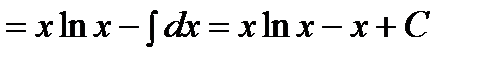 .
. .
.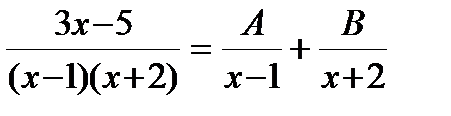 .
.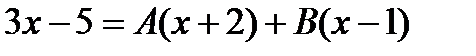 .
.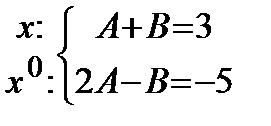 .
.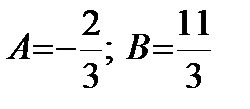 .
.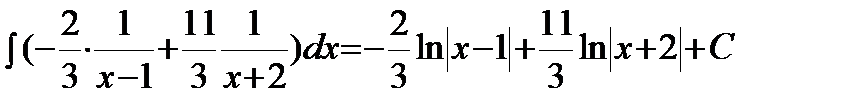 .
.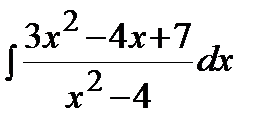 .
.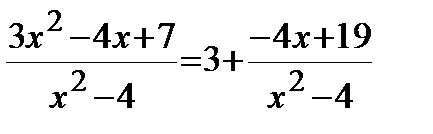 .
.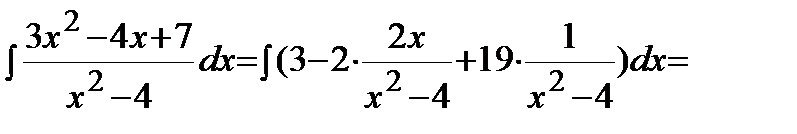
 .
. .
.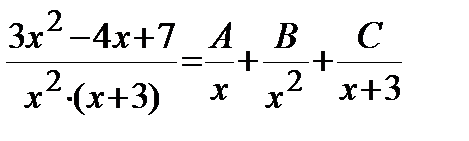 .
.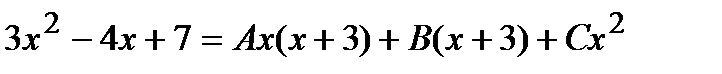 .
.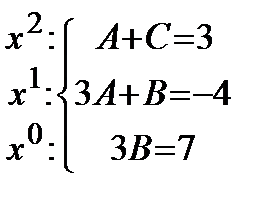 .
.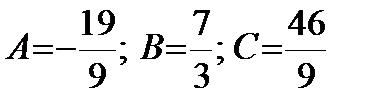 .
. .
.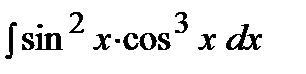 .
.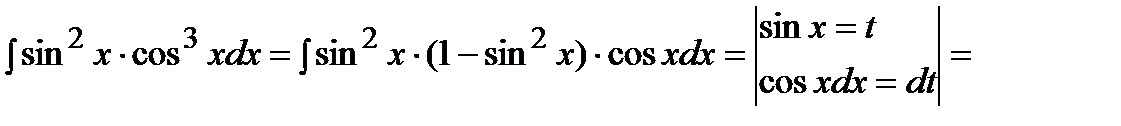
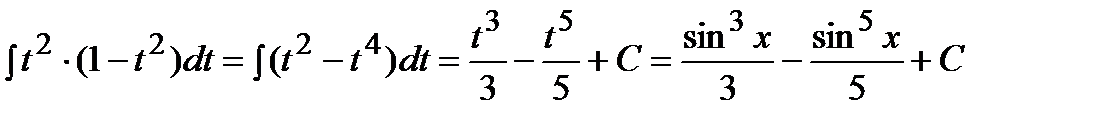 .
. .
.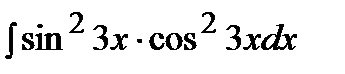 .
.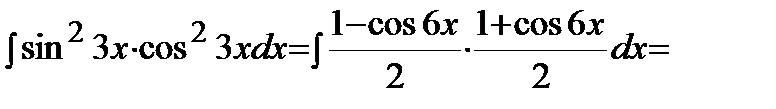
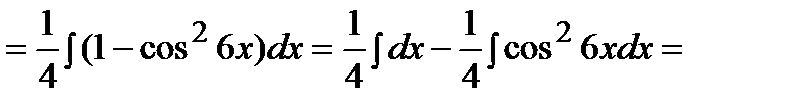
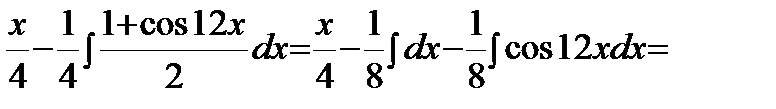
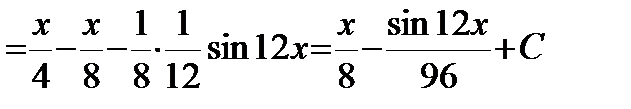 .
.


