
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы и линейные операции над нимиСодержание книги
Поиск на нашем сайте
В геометрии вектором называют направленный отрезок Длиной (или модулем) Векторы, параллельные одной прямой, называются коллинеарными и компланарными, если они параллельны одной плоскости. Если вектор Для векторов вводятся операции сложения и вычитания. При этом заметим, что знаки «+» и «-», которые ставятся между векторами, имеют другой смысл, чем в алгебре: они обозначают не алгебраическое, а геометрическое сложение векторов по правилу треугольника или параллелограмма. Произведением вектора Сложение векторов и умножение их на число называются линейными операциями над векторами. Эти операции обладают свойствами по форме аналогичными свойствам сложения и умножения чисел.
Если в прямоугольной системе координат точки А и В имеют координаты
а модуль его определяется как расстояние между двумя точками:
Линейные операции над векторами, заданными своими координатами 1) при сложении двух векторов их одноименные координаты складываются: 2) при умножении вектора Два вектора равны, если равны их соответствующие координаты, т.е. Два вектора коллинеарные, если их координаты пропорциональны. Итак, если
Умножение векторов Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор. Скалярным произведением Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел. Векторным произведением двух векторов 1) имеет модуль, численно равный площади параллелограмма, построенного на векторах 2) перпендикулярен к плоскости этого параллелограмма; 3) направлен в такую сторону, с которой кратчайший поворот от Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно.В результате получают число. Смешанное произведение трех векторов Пусть заданы два вектора Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:
Угол между векторами вычисляется по формуле
или в координатной форме Условием перпендикулярности ненулевых векторов
Векторное произведение ненулевых векторов
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. Скаляр
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности:
Задача. Определить внутренние углы Решение. Найдем
Легко видеть, что
Отсюда Аналогично, находя предварительно, что
Отсюда
Задача. Вычислить площадь треугольника с вершинами Решение. Найдем вначале площадь
Тогда Следовательно,
Задача. Вычислить объем пирамиды с вершинами Решение. Найдем координаты векторов Тогда
Следовательно,
|
||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.131.51 (0.006 с.) |

 с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Таким образом, считается, что два направленных отрезка
с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Таким образом, считается, что два направленных отрезка  и
и  , имеющие равные длины и одно и то же направление, определяют (изображают) один и тот же вектор
, имеющие равные длины и одно и то же направление, определяют (изображают) один и тот же вектор  , и пишут
, и пишут  .
. вектора
вектора  называется число, равное длине отрезка АВ, изображающего вектор.
называется число, равное длине отрезка АВ, изображающего вектор.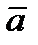 изображается направленным отрезком
изображается направленным отрезком 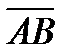 , то вектор, изображаемый направленным отрезком
, то вектор, изображаемый направленным отрезком 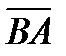 , называется вектором, противоположным вектору
, называется вектором, противоположным вектору  и обозначается -
и обозначается -  .
. на число
на число 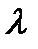 называется вектор
называется вектор  , имеющий длину
, имеющий длину 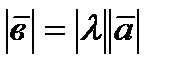
 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора  , если
, если  , и противоположно ему, если
, и противоположно ему, если  .
. и
и 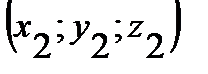 , то координаты вектора
, то координаты вектора  находятся как разности соответствующих координат конца В и начала А этого вектора, т.е.
находятся как разности соответствующих координат конца В и начала А этого вектора, т.е. ,
, .
. и
и  , выполняются по следующим правилам:
, выполняются по следующим правилам: ;
; на число
на число  все его координаты умножаются на это число:
все его координаты умножаются на это число:  .
. .
. ½½
½½  , то
, то  или
или 
 .
. двух ненулевых векторов
двух ненулевых векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: 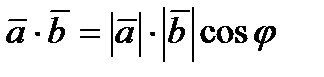 , где
, где  .
. и
и  называется вектор
называется вектор  , который:
, который: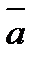 и
и  :
:  ;
; к
к  рассматривается совершающимся против часовой стрелки (такое расположение векторов
рассматривается совершающимся против часовой стрелки (такое расположение векторов  ,
,  и
и  называется правой тройкой векторов).
называется правой тройкой векторов). .
. ,
,  и
и  , которое обозначается
, которое обозначается  или
или  , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах
, есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах  ,
,  и
и  , как на ребрах.
, как на ребрах. и
и  .
. .
. ,
, .
. и
и  является равенство нулю их скалярного произведения:
является равенство нулю их скалярного произведения: .
. выражается через координаты данных векторов
выражается через координаты данных векторов  и
и  следующим образом:
следующим образом: .
.

 ½½
½½  .
. , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
, представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов: .
. .
. c вершинами
c вершинами  .
.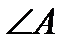 . Для этого надо найти векторы
. Для этого надо найти векторы  и
и  . Зная векторы
. Зная векторы 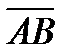 и
и  , из формулы (2) получим
, из формулы (2) получим
 . Тогда
. Тогда .
. .
. , получим
, получим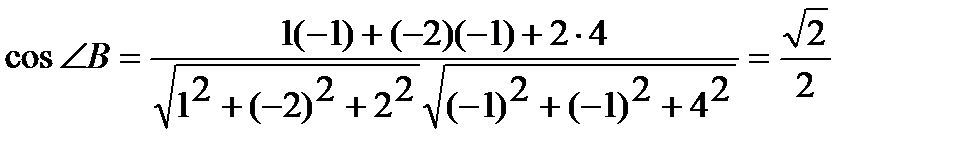 .
. и
и  .
. .
. параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  как на сторонах. По определению векторного произведения
как на сторонах. По определению векторного произведения  . Но
. Но
 .
. .
. .
.
 .
. . Очевидно, что
. Очевидно, что  .
. . Но
. Но 
 ..
.. .
.


