
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интеграла II рода от пути интегрированияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть
Сформулируем в виде теоремы без доказательства условия, при которых криволинейный интеграл II рода не зависит от пути интегрирования. Теорема 2.3 (признак независимости криволинейный интеграл II рода от пути интегрирования). Для того, чтобы криволинейный интеграл II рода
Пример 5. Вычислить w Решение. Так как
Рис. 2.7
Следовательно, по свойству 4 криволинейного интеграла II рода (п. 2.3) имеем Ответ: Рассмотрим еще две теоремы.
Терема 2.4. Если выполняется условие (2.21), то подынтегральное выражение
Тогда из равенства (2.22), согласно (2.20) и свойства определенного интеграла, получим:
т. е. Формула (2.23) называется обобщенной формулой Ньютона-Лейб-ница для криволинейного интеграла II рода от полного дифференциала. Теорема 2.5. Если подынтегральное выражение
Замечания 1. Утверждения, сформулированные в теоремах 2.3 – 2.5, равно- сильны между собой, то есть, выполнение любого из них влечет за собой выполнение остальных. 2. Чтобы не путать переменную интегрирования
3. Функцию
В качестве начальной точки 4. Аналогичные результаты справедливы для криволинейного интеграла II рода
Пример 6. Показать, что выражение w Решение. Проверим выполнимость условия (2.21). Так как Пусть
Ответ: Самостоятельная работа 1. Вычислить: а) в) д) е) 2. Показать, что данное выражение является полным дифференциалом некоторой функции а) б) в) г) е)
Основные приложения криволинейного Интеграла II рода
Площадь плоской фигуры Из теоремы 2.2 следует, что если в формуле Остроградского-Грина (2.19) подобрать функции
Складывая почленно эти равенства, будем иметь:
Таким образом, площадь Замечания 1. Подынтегральное выражение в формуле (2.31) легко запомнить, если его записать в виде определителя 2-го порядка 2. Формула (2.31) наиболее удобна и часто используется при решении задач. Пример 7. Вычислить площадь фигуры, ограниченной петлей кривой w Решение. Перейдем к параметрическим уравнениям данной кривой, положив
то получим:
Рис. 2.8
Ответ: Работа переменной силы. Как отмечалось ранее (п. 2.2), переменная сила
Если сила
Пример 8. Вычислить работу силы w Решение. По формуле (2.5) получим:
Ответ: Самостоятельная работа 1. С помощью криволинейного интеграла II рода найти площадь фигур, ограниченных линиями: а) первой аркой циклоиды б) астроидой в) эллипсом г) кардиоидой д) лемнискатой Бернулли е) 2. Вычислить работу силы 3. Вычислить работу силы 4. Вычислить работу силы 5. Вычислить работу силы 6. Вычислить работу силы 3. Индивидуальные задания для контрольной Работы 1. Вычислить работу силы 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 2. Показать, что данное выражение является полным дифференциалом функции 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Список литературы
1. Выгодский, М. Я. Справочник по высшей математике / М. Я. Выгодский. – М.: АСТ: Астрель, 2006. – 991 с. 2. Каплан, И. А. Практические занятия по высшей математике. Ч. IV / И. А. Каплан. – Харьков: Из-во Гос. ун-та им. А. М. Горького, 1966. – 236 с. 3. Кратные и криволинейные интегралы: методич. указ. / Сост. В. А. Меркулов. – Волгоград: ВолгИСИ, 1992. – 46 с. 4. Лунгу, К. Н. Сборник задач по высшей математике. 2 курс / К. Н. Лунгу [и др.]; под ред. С. Н. Федина. – М.: Айрис-пресс, 2004. – 592 с.: ил. – (Высшее образование). 5. Меркулов, В. А. Курс высшей математики. Избранные разделы. Раздел 1: Аналитическая геометрия: учеб. пособие / В. А. Меркулов. – Волгоград, 2004. – 88 с. 6. Письменный, Д. Т. Конспект лекций по высшей математике. Ч. 2 / Д. Т. Письменный. – М.: Рольф, 2001. – 256 с. 7. Рябушко, А. П. Сборник индивидуальных заданий по высшей математике. В 3-х ч. Ч. III / А. П. Рябушко [и др.]. – Минск: Вышэйшая школа, 1991. – 288 с.
Приложения Приложение 1
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.32.78 (0.011 с.) |

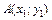 и
и 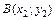 – две произвольные точки односвязной области
– две произвольные точки односвязной области  плоскости
плоскости 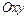 . Точки
. Точки  и
и 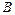 можно соединить различными линиями. По каждой из этих кривых интеграл
можно соединить различными линиями. По каждой из этих кривых интеграл 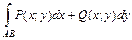 имеет различные значения. Если же его значения по всевозможным кривым
имеет различные значения. Если же его значения по всевозможным кривым 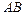 одинаковы, то говорят, что интеграл не зависит от пути интегрирования. В этом случае для интеграла достаточно отметить лишь его начальную точку
одинаковы, то говорят, что интеграл не зависит от пути интегрирования. В этом случае для интеграла достаточно отметить лишь его начальную точку 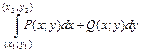 . (2.20)
. (2.20)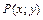 и
и  непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие:
непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие: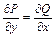 . (2.21)
. (2.21) .
. , а
, а 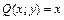 , то
, то 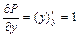 и
и 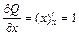 , тогда
, тогда  к точке
к точке  будем двигаться по отрезкам, параллельным координатным осям (рис. 2.7), так как вычисление исходного интеграла в этом случае самое простое (п. 2.4).
будем двигаться по отрезкам, параллельным координатным осям (рис. 2.7), так как вычисление исходного интеграла в этом случае самое простое (п. 2.4).
 . Так как отрезок
. Так как отрезок  задается уравнением
задается уравнением 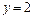 , то
, то 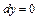 , а
, а 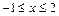 , поэтому
, поэтому 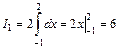 . Так как отрезок
. Так как отрезок 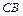 задается уравнением
задается уравнением 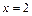 , то
, то  , а
, а 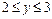 , тогда
, тогда 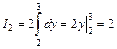 . Окончательно имеем:
. Окончательно имеем:  .
. . t
. t является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции  , т. е. имеет место равенство:
, т. е. имеет место равенство: . (2.22)
. (2.22)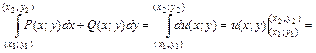
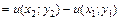 ,
, . (2.23)
. (2.23) +
+ 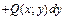 есть полный дифференциал и путь интегрирования
есть полный дифференциал и путь интегрирования  – замкнутая кривая, то
– замкнутая кривая, то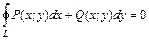 . (2.24)
. (2.24)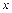 с верхним пределом
с верхним пределом 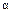 ,
, 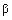 ,
, 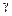 и т. д.).
и т. д.). . (2.25)
. (2.25)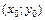 обычно берут начало координат
обычно берут начало координат  .
.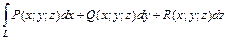 по пространственной кривой
по пространственной кривой 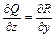 ,
,  , (2.26)
, (2.26) , (2.27)
, (2.27)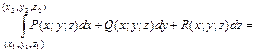
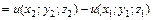 , (2.28)
, (2.28) (2.29)
(2.29) является полным дифференциалом функции
является полным дифференциалом функции 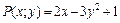 , то
, то  и так как
и так как  , то
, то 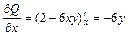 . Следовательно, условие (2.21) выполняется и по теореме 2.4 исходное выражение является дифференциалом некоторой функции
. Следовательно, условие (2.21) выполняется и по теореме 2.4 исходное выражение является дифференциалом некоторой функции  и
и 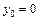 , тогда:
, тогда:
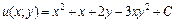 . t
. t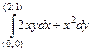 ; б)
; б)  ;
;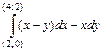 ; г)
; г)  ;
; ;
;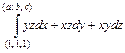 ; ж)
; ж) 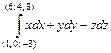 .
.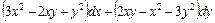 ;
;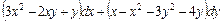 ;
;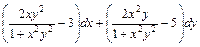 ;
;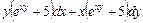 ;
;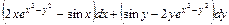 ;
;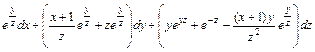 .
. , то, как известно, двойной интеграл в формуле (2.19) будет определять площадь
, то, как известно, двойной интеграл в формуле (2.19) будет определять площадь  области
области 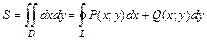 , где
, где  и
и  и
и 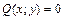 . В обоих случаях получим:
. В обоих случаях получим: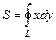 и
и 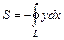 . (2.30)
. (2.30)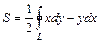 . (2.31)
. (2.31)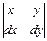 .
.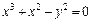 (рис. 2.8).
(рис. 2.8).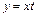 . Подставив
. Подставив 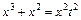 , т. е
, т. е  , тогда
, тогда  . Петля замыкается в точке с абсциссой
. Петля замыкается в точке с абсциссой 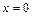 , откуда находим
, откуда находим 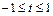 . Искомую площадь определим по формуле (2.30), где рассуждения проведем, используя формулу (2.9). Так как
. Искомую площадь определим по формуле (2.30), где рассуждения проведем, используя формулу (2.9). Так как  и
и  ,
,

 .
.
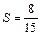 кв. ед. t
кв. ед. t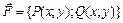 на криволинейном участке
на криволинейном участке 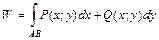 .
. задана по пространственной кривой
задана по пространственной кривой  .
.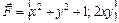 вдоль дуги параболы
вдоль дуги параболы 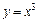 , заключенной между точками
, заключенной между точками  и
и  .
. . Воспользуемся формулой (2.13):
. Воспользуемся формулой (2.13):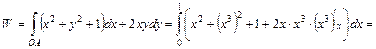
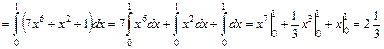 .
. Дж. t
Дж. t и осью
и осью  ;
;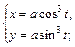
 ;
;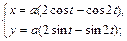
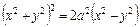 ;
;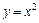 и
и  .
. , совершаемую по прямой от точки
, совершаемую по прямой от точки 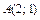 .
. при перемещении материальной точки по прямой
при перемещении материальной точки по прямой 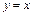 от точки
от точки 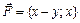 при перемещении материальной точки вдоль контура квадрата, образованного прямыми
при перемещении материальной точки вдоль контура квадрата, образованного прямыми 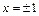 ,
,  .
.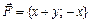 при перемещении материальной точки вдоль окружности
при перемещении материальной точки вдоль окружности 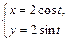 по ходу часовой стрелки.
по ходу часовой стрелки.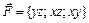 вдоль отрезка прямой
вдоль отрезка прямой 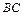 , если
, если  и
и  .
.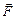 при перемещении точки вдоль дуги линии
при перемещении точки вдоль дуги линии 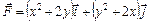 ,
, 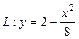 , расположенная во втором координатном углу, в направлении против часовой стрелки.
, расположенная во втором координатном углу, в направлении против часовой стрелки. ,
,  в направлении против часовой стрелки.
в направлении против часовой стрелки.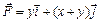 ,
, 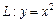 от точки
от точки  до точки
до точки 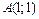 .
. ,
, 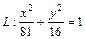 в направлении против часовой стрелки.
в направлении против часовой стрелки. ,
, 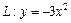 от точки
от точки  .
. ,
,  в направлении против часовой стрелки.
в направлении против часовой стрелки.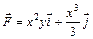 ,
,  от точки
от точки 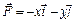 ,
, 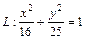 в направлении против часовой стрелки.
в направлении против часовой стрелки.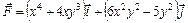 ,
, 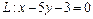 от точки
от точки 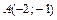 до точки
до точки 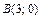 .
. ,
, 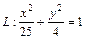 , расположенная в первой координатной четверти, в направлении против часовой стрелки.
, расположенная в первой координатной четверти, в направлении против часовой стрелки. ;
; ;
; ;
;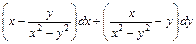 ;
;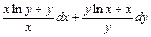 ;
;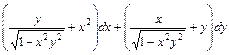 ;
; ;
;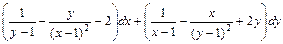 ;
;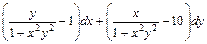 ;
; .
.


