
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волжский институт строительства и технологийСтр 1 из 6Следующая ⇒
Волжский институт строительства и технологий (филиал) Волгоградского государственного архитектурно-строительного университета
Кафедра высшей математики ПРЯМОЛИНЕЙНО О КРИВОЛИНЕЙНЫХ Методические указания для студентов Очной и заочной форм обучения по дисциплине «Высшая математика»
Волжский 2008 УДК 517.3
Прямолинейно о криволинейных интегралах: метод. указ. для студентов очной и заочной форм обучения по дисц. «Высшая математика» / ВИСТех (филиал) ВолгГАСУ; [Е. В. Абрамов, Е. Д. Илларионова]. – Волжский: ВИСТех (филиал) ВолгГАСУ, 2008. – 61 с.
Изложен основной теоретический материал, приведены примеры решения задач и задания для самостоятельной работы по каждому разделу. Включены задания для контрольной работы. Материалы могут быть использованы при самостоятельной подготовке по разделу «Криволинейные интегралы». Данные методические указания предназначены для студентов 1-го курса очной и заочной форм обучения по дисциплине «Высшая математика».
Ил. 53 Библиогр. 7 назв.
Криволинейный интеграл I рода
Основные понятия Обобщением определенного интеграла на случай, когда областью интегрирования выступает не отрезок, а некоторая кривая, является криволинейный интеграл. Пусть на плоскости
которая называется интегральной суммой для функции
Рис. 1.1
Таким образом, по определению:
Аналогично определяется криволинейный интеграл I рода от функции трех переменных
Если кривая интегрирования Теорема 1.1. (существования криволинейного интеграла I рода). Если функция
Геометрический и физический смысл криволинейного Интеграла I рода
Рассмотрим две задачи, приводящие к понятию криволинейного интеграла I рода по плоской кривой. Площадь цилиндрической поверхности Пусть в координатной плоскости
В этом состоит геометрический смысл криволинейного интеграла I рода.
Рис. 1.2
Масса материальной кривой (цепь, провод, трос, канат и т. д.). Пусть дана материальная кривая
Если кривая
Таким образом, криволинейный интеграл I рода по кривой Замечание. Аналогичные рассуждения и формулы справедливы и для пространственной кривой интегрирования.
Интеграла I рода Криволинейный интеграл I рода имеет разнообразные приложения в математике и физике. Рассмотрим основные из них без доказательств.
Длина кривой Если повторить рассуждения п. 1.1 и в интеграле (1.2) положить
которое справедливо при любом способе задания кривой. При решении задач при конкретном способе задания кривой Пример 5. Найти длину дуги w Решение. Длину дуги вычислим по формуле (1.13): Получим:
Ответ: Площадь цилиндрической поверхности Как уже отмечалось (п. 1.2), площадь цилиндрической поверхности
Пример 6. Вычислить площадь части цилиндрической поверхности w Решение. Искомая площадь части цилиндрической поверхности по формуле (1.13) выражается интегралом
Ответ:
Рис. 1.4
Замечания 1. Если цилиндрическая поверхность целиком лежит ниже координатной плоскости 2. Если цилиндрическая поверхность располагается так, что часть ее лежит выше плоскости Масса кривой Как уже отмечалось (п. 1.2), масса материальной плоской кривой
где Если кривая
где В случае, когда кривая интегрирования однородна, то ее плотность Пример 7. Вычислить массу материальной дуги w Решение. Согласно формуле (1.6) получим: Ответ: Пример 8. Вычислить массу дуги кривой, заданной уравнениями w Решение. Согласно формуле (1.14) искомая масса выражается интегралом:
Ответ: Статические моменты кривой Статическим моментом Аналогично определяется статический момент Статические моменты системы материальных точек определяются как суммы соответствующих статических моментов точек этой системы. Статические моменты точки и системы точек относительно координатных плоскостей Если масса распределена непрерывно вдоль материальной плоской кривой
Для пространственной кривой имеют место аналогичные формулы вычисления статических моментов относительно координатных плоскостей
и Если материальная кривая Пример 9. Вычислить статические моменты относительно координатных осей прямолинейного отрезка w Решение. Так как Определим статический момент относительно оси Легко видеть, что Ответ: Координаты центра тяжести кривой Центром тяжести плоской кривой называется точка Координаты центра тяжести пространственной кривой определяются аналогично центру тяжести плоской кривой. Координаты центра тяжести
где Если кривая интегрирования является однородной, то, как уже отмечалось, в формулах (1.15) и (1.6) ее плотность Для пространственной кривой формулы нахождения координат центра тяжести
где
Если пространственная кривая Пример 10. Определить центр тяжести однородной дуги астроиды w Решение. Пусть Определим по соответствующей формуле (1.15) статический момент относительно оси
Таким образом, по соответствующей формуле (1.17) получаем:
Аналогично рассуждая, найдем статический момент соответствующую формулу (1.15):
Ответ: Моменты инерции кривой Моментом инерции материальной точки массы Момент инерции материальной точки относительно оси Для материальной пространственной кривой АВ, имеющей плотность
и Заметим, что моменты инерции в пространстве связаны следующими соотношениями:
Если кривая
и Если материальная кривая Пример 11. Найти моменты инерции относительно осей координат отрезка однородной прямой
Рис. 1.5
w Решение. По условию Вычислим первый интеграл. Для этого, согласно формуле (1.9), преобразуем подынтегральную функцию:
Рассуждая аналогично для второго интеграла, получим:
Ответ:
Самостоятельная работа 1. Вычислить длину дуги кривой 2. Вычислить длину дуги цепной линии 3. Вычислить длину кардиоиды 4. Найти длину первого витка винтовой линии 5. Вычислить площадь боковой поверхности цилиндра 6. Вычислить площадь цилиндрической поверхности с направляющей 7. Вычислить площадь цилиндрической поверхности с направляющей 8. Вычислить площадь боковой поверхности параболического цилиндра 9. Найти массу четверти однородной окружности 10. Вычислить массу дуги кривой 11. Вычислить массу дуги кривой 12. Вычислить массу дуги конической винтовой линии 13. Вычислить статические моменты относительно координатных осей однородной дуги астроиды 14. Найти статический момент относительно оси 15. Найти статический момент относительно оси
16. Найти декартовые координаты центра масс первой полуарки циклоиды 17. Найти координаты центра тяжести дуги однородной кривой 18. Найти декартовые координаты центра тяжести дуги однородной кривой 19. Вычислить декартовые координаты центра масс дуги первого витка винтовой линии 20. Вычислить моменты инерции относительно координатных осей дуги четверти однородной окружности 21. Вычислить момент инерции относительно оси абсциссами 22. Найти момент инерции относительно оси
Основные понятия Криволинейный интеграл II рода определяется почти так же, как и криволинейный интеграл I рода. Пусть в плоскости Таким образом, по определению, Аналогично вводится криволинейный интеграл II рода по координате
где
Криволинейный интеграл II рода общего вида
Криволинейный интеграл II рода общего вида
по пространственной кривой
Рис.2.1
Теорема 2.1 (существование криволинейного интеграла II рода). Если кривая
Интеграла II рода Рассмотрим основные свойства криволинейного интеграла II рода без доказательств, которые обобщают соответствующие свойства определенного интеграла. Пусть функции 1. При изменении направления пути интегрирования криволинейный интеграл II рода меняет свой знак на противоположный, т. е. 2. где
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.140.108 (0.122 с.) |
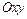 в декартовой прямоугольной системе координат задана непрерывная кривая
в декартовой прямоугольной системе координат задана непрерывная кривая 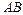 (или
(или  ) длины
) длины 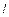 , в точках которой определена некоторая непрерывная функция
, в точках которой определена некоторая непрерывная функция 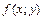 . Разобьем кривую
. Разобьем кривую 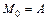 ,
, 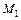 ,
, 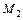 , …,
, …, 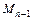 ,
, 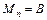 на
на 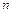 произвольных дуг
произвольных дуг 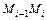 с длинами
с длинами  соответственно (
соответственно (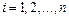 ) (рис. 1.1). Выберем на каждой дуге произвольно точку
) (рис. 1.1). Выберем на каждой дуге произвольно точку 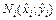 и составим сумму произведений
и составим сумму произведений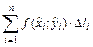 , (1.1)
, (1.1)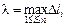 – наибольшая из длин дуг деления. Если при
– наибольшая из длин дуг деления. Если при 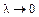 (т. е. при
(т. е. при 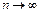 ) существует конечный предел интегральных сумм вида (1.1), не зависящий ни от способа разбиения кривой
) существует конечный предел интегральных сумм вида (1.1), не зависящий ни от способа разбиения кривой 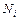 на них, то этот предел называют криволинейным интегралом I рода от функции
на них, то этот предел называют криволинейным интегралом I рода от функции 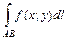 (или
(или  ), где
), где 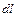 – дифференциал дуги кривой
– дифференциал дуги кривой 
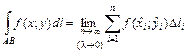 . (1.2)
. (1.2)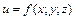 по пространственной кривой
по пространственной кривой 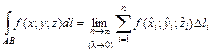 . (1.3)
. (1.3) (или
(или  ).
).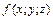 ) непрерывна в каждой точке гладкой[1] кривой, то криволинейный интеграл I рода вида (1.2) (или (1.3)) существует.
) непрерывна в каждой точке гладкой[1] кривой, то криволинейный интеграл I рода вида (1.2) (или (1.3)) существует.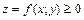 . Тогда можно построить цилиндрическую поверхность: направляющей цилиндрической поверхности служит данная кривая
. Тогда можно построить цилиндрическую поверхность: направляющей цилиндрической поверхности служит данная кривая  и цилиндрическая поверхность заключена между кривой
и цилиндрическая поверхность заключена между кривой  (рис. 1.2). Площадь такой цилиндрической поверхности находится по формуле:
(рис. 1.2). Площадь такой цилиндрической поверхности находится по формуле: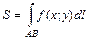 . (1.4)
. (1.4)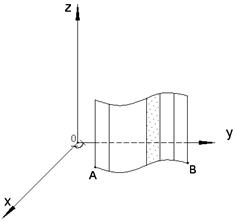
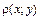 . Разобьем ее на
. Разобьем ее на 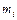 дуги
дуги 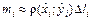 . Суммируя, находим приближенное значение массы
. Суммируя, находим приближенное значение массы 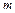 всей кривой
всей кривой  . (1.5)
. (1.5) (т. е.
(т. е.  , или, согласно формуле (1.2), получим:
, или, согласно формуле (1.2), получим: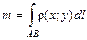 . (1.6)
. (1.6)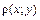 , в чем и состоит механический смысл криволинейного интеграла I рода по кривой
, в чем и состоит механический смысл криволинейного интеграла I рода по кривой 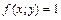 всюду на кривой
всюду на кривой 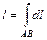 , (1.13)
, (1.13) .
.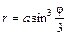 от
от 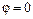 до
до 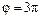 .
. . Для вычисления этого интеграла воспользуемся формулой (1.12), где
. Для вычисления этого интеграла воспользуемся формулой (1.12), где 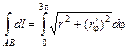 . Так как
. Так как 
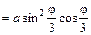 , то
, то 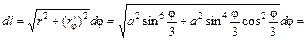
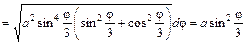 .
.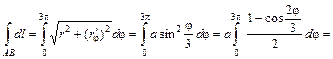
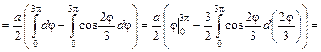
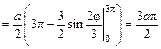 .
.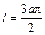 ед. длины. t
ед. длины. t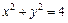 , заключенной между плоскостью
, заключенной между плоскостью 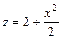 (рис. 1.4).
(рис. 1.4).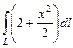 , где направляющая
, где направляющая 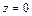 ). Уравнение окружности запишем в параметрическом виде:
). Уравнение окружности запишем в параметрическом виде:  где
где  . Воспользуемся формулой (1.7). Подынтегральная функция примет вид:
. Воспользуемся формулой (1.7). Подынтегральная функция примет вид:  . Так как
. Так как 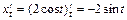 , а
, а 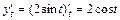 , то
, то 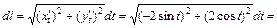
 . Согласно формуле (1.7) имеем:
. Согласно формуле (1.7) имеем: 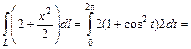
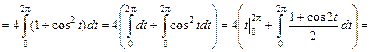
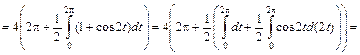
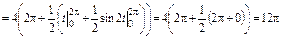 .
. кв. ед. t
кв. ед. t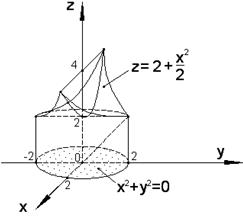
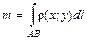 ,
,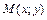 .
.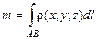 , (1.14)
, (1.14)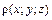 – плотность кривой в точке
– плотность кривой в точке 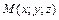 .
.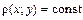 (или
(или 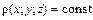 ).
). ,
, 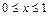 , плотность которой
, плотность которой 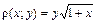 .
.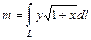 . Для решения данного криволинейного интеграла I рода воспользуемся формулой (1.9). Для этого в подынтегральной функции заменим
. Для решения данного криволинейного интеграла I рода воспользуемся формулой (1.9). Для этого в подынтегральной функции заменим 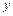 на
на 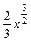 . Так как
. Так как  , то
, то 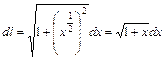 . Подставляя полученные значения, получим:
. Подставляя полученные значения, получим: 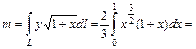
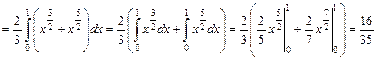 .
.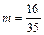 ед. массы. t
ед. массы. t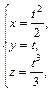
 , если плотность в каждой ее точке равна
, если плотность в каждой ее точке равна 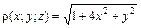 .
.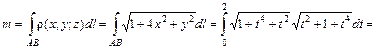
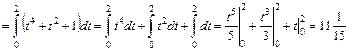 .
. ед. массы. t
ед. массы. t относительно оси
относительно оси  материальной точки
материальной точки 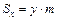 .
. относительно оси
относительно оси 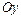 :
: 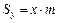 .
.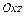 и
и 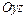 в пространстве
в пространстве 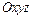 определяются аналогично статическим моментам точки и системы точек относительно координатных осей
определяются аналогично статическим моментам точки и системы точек относительно координатных осей 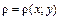 в каждой точке этой кривой, то статические моменты
в каждой точке этой кривой, то статические моменты  и
и 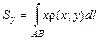 . (1.15)
. (1.15)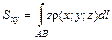 ,
, 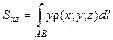
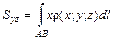 . (1.16)
. (1.16) и
и 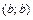 (
( ). Плотность в каждой точке отрезка равна произведению координат этой точки.
). Плотность в каждой точке отрезка равна произведению координат этой точки.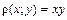 , то по формулам (1.15) имеем:
, то по формулам (1.15) имеем:  и
и  . Понятно, что уравнение отрезка
. Понятно, что уравнение отрезка 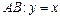 , поэтому воспользуемся формулой (1.9).
, поэтому воспользуемся формулой (1.9).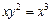 , а
, а 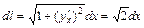 . Получим:
. Получим: 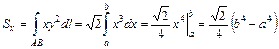 .
.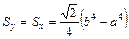 .
.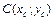 плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой относительно той же оси.
плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой относительно той же оси. материальной плоской кривой
материальной плоской кривой  и
и 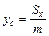 , (1.17)
, (1.17)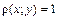 .
.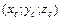 имеют вид:
имеют вид: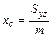 ,
, 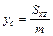 и
и 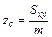 , (1.18)
, (1.18)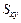 ,
, 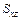 ,
,  – статические моменты пространственной кривой относительно координатных плоскостей, вычисляемые по формулам (1.16) соответственно, а
– статические моменты пространственной кривой относительно координатных плоскостей, вычисляемые по формулам (1.16) соответственно, а  .
.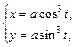 лежащей в первой четверти (
лежащей в первой четверти ( ).
).
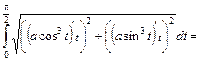

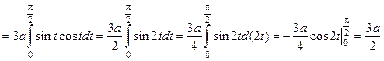 .
.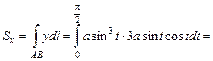
 .
. .
.
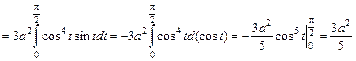 . Следовательно, по соответствующей формуле (1.17):
. Следовательно, по соответствующей формуле (1.17): 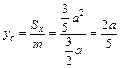 .
.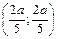 . t
. t точки до оси, т. е.
точки до оси, т. е. 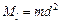 .
.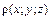 , моменты инерции относительно координатных осей
, моменты инерции относительно координатных осей 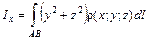 ,
, 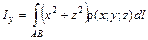 ,
, 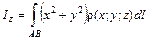 ,
,  ,
,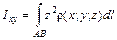 ,
, 
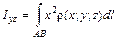 . (1.19)
. (1.19)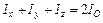 ,
, 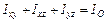 . (1.20)
. (1.20)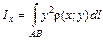 ,
, 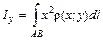
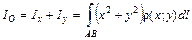 . (1.21)
. (1.21) , лежащего между этими осями (рис. 1.5).
, лежащего между этими осями (рис. 1.5).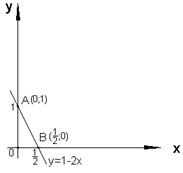
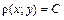 , где
, где 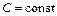 . По соответствующим формулам (1.21) имеем:
. По соответствующим формулам (1.21) имеем:  и
и 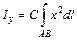 . По рисунку видно, что
. По рисунку видно, что 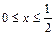 .
.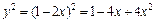 и найдем дифференциал дуги кривой:
и найдем дифференциал дуги кривой: 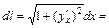
 . Получим:
. Получим: 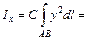

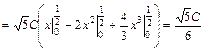 .
.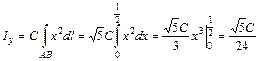 .
. ,
, 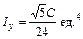 t
t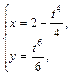 ограниченной точками пересечения ее с осями координат (
ограниченной точками пересечения ее с осями координат (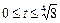 ).
).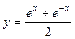 ,
,  .
. .
.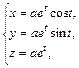
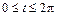 .
.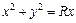 , заключенной внутри сферы
, заключенной внутри сферы  .
. где
где 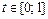 , ограниченной снизу плоскостью
, ограниченной снизу плоскостью 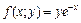 .
. и
и 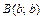 , ограниченной снизу плоскостью
, ограниченной снизу плоскостью  .
.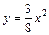 , ограниченной плоскостями
, ограниченной плоскостями 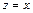 ,
,  и
и 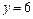 .
.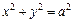 , лежащей в первом квадранте.
, лежащей в первом квадранте.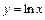 , если плотность дуги в каждой точке равна квадрату абсциссы этой точки и
, если плотность дуги в каждой точке равна квадрату абсциссы этой точки и 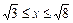 .
.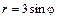 (
(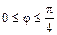 ), если плотность в каждой ее точке пропорциональна расстоянию до полюса.
), если плотность в каждой ее точке пропорциональна расстоянию до полюса.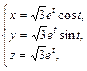
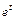 .
. расположенной в первом квадранте.
расположенной в первом квадранте.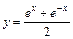 (
(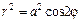 от
от 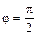 .
. где
где  .
.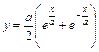 ,
, 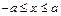 .
.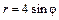 , если
, если  .
. если плотность в каждой ее точке пропорциональна аппликате точки.
если плотность в каждой ее точке пропорциональна аппликате точки. лежащей в первом квадранте.
лежащей в первом квадранте. , заключенной между точками с
, заключенной между точками с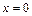 и
и 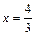 .
.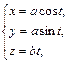 где
где  , определенная в каждой точке кривой. Разобьем кривую
, определенная в каждой точке кривой. Разобьем кривую  к точке
к точке 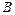 на
на 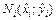 и составим сумму произведений вида
и составим сумму произведений вида 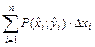 (2.1), где
(2.1), где 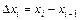 – проекция дуги
– проекция дуги 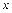 . Таких сумм можно составить бесчисленное множество. Если при
. Таких сумм можно составить бесчисленное множество. Если при 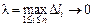 интегральные суммы вида (2.1) имеют конечный предел, не зависящий ни от способа разбиения кривой
интегральные суммы вида (2.1) имеют конечный предел, не зависящий ни от способа разбиения кривой 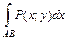 (или
(или 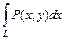 ).
). .
. по кривой
по кривой 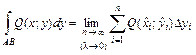 ,
,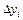 – проекция дуги
– проекция дуги 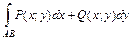 по кривой
по кривой 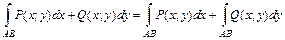 . (2.2)
. (2.2)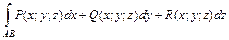 (2.3)
(2.3)
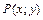 ,
,  ,
, 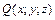 ,
,  ) непрерывны по кривой
) непрерывны по кривой 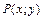 и
и  .
.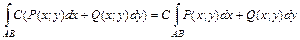 ,
, .
.


