
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление криволинейного интеграла I родаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вычисление криволинейного интеграла I рода зависит от способа задания кривой (явное, параметрическое или полярное) и сводится к вычислению определенного интеграла. Параметрическое представление кривой интегрирования Если кривая
На практике использование формулы (1.7) осуществляется следующим образом: в подынтегральной функции Пример 1. Вычислить w Решение. Воспользуемся формулой (1.7). Для этого в подынтегральной функции Используя проведенные рассуждения, получим:
Ответ: При задании кривой
Пример 2. Вычислить w Решение. Воспользуемся формулой (1.8). Преобразуем подынтегральную функцию:
Ответ: Замечание. При вычислении интегралов от тригонометрических функций полезно помнить несколько приемов, которые позволяют значительно облегчить решение задачи. Например, в выражении Чтобы избавится от квадратного корня в выражении
Аналогичные рассуждения проводят для выражения Явное задание кривой интегрирования
Пусть кривая
Если уравнения
Заметим, что формула (1.9) является частным случаем формулы (1.7), где в качестве параметра На практике использование формулы (1.9) или (1.10) аналогично использованию формул (1.7) или (1.8) соответственно. Пример 3. Вычислить w Решение. В подынтегральной функции
Ответ: Полярное задание кривой интегрирования Напомним, что полярная система координат на плоскости задается точкой
Рис. 1.3
Если декартовую прямоугольную систему координат совместить с полярной системой координат так, что бы полюс попал в начало координат, полярная ось совпала с осью абсцисс (включая положительные направления) и выбрать одинаковый масштаб, то получим, что декартовые и полярные координаты связана между собой по правилам: Если кривая
Формула (1.12) получается из формулы (1.7), если в качестве параметра выбрать угол На практике проводят рассуждения, аналогичные вышеуказанным: в подынтегральной функции переменные Пример 4. Вычислить w Решение. Выполним знакомые рассуждения. Сначала преобразуем подынтегральную функцию:
Так как Таким образом, по формуле (1.12) получим:
Ответ: Самостоятельная работа 1. Вычислить 2. Вычислить 3. Вычислить 4. Переходя к параметрическому заданию кривой 5. Вычислить 6. Вычислить 7. Вычислить 8. Вычислить 9. Вычислить 10. Вычислить 11. Вычислить 12. Вычислить 13. Вычислить 14. Вычислить 15. Вычислить 16. Вычислить 17. Вычислить
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 5788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.12.236 (0.011 с.) |

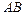 .
. где
где  (
( ) и
) и 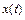 ,
,  – непрерывно дифференцируемые функции параметра
– непрерывно дифференцируемые функции параметра 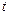 на отрезке
на отрезке  , причем точке
, причем точке  соответствует
соответствует 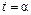 , а точке
, а точке 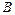 – значение
– значение 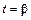 , тогда криволинейный интеграл I рода вычисляется по правилу:
, тогда криволинейный интеграл I рода вычисляется по правилу: . (1.7)
. (1.7) переменные
переменные 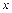 и
и 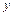 меняются на переменную
меняются на переменную  и
и  соответственно, а дифференциал дуги кривой
соответственно, а дифференциал дуги кривой 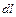 на
на  и расставляются пределы интегрирования
и расставляются пределы интегрирования 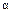 и
и 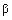 по переменной
по переменной  , если
, если  – первая арка циклоиды
– первая арка циклоиды  (
( ).
). заменим
заменим  :
:  . Так как
. Так как  , а
, а  , то
, то 
 . Чтобы построить первую арку циклоиды, параметр
. Чтобы построить первую арку циклоиды, параметр 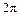 – это и есть пределы интегрирования в определенном интеграле.
– это и есть пределы интегрирования в определенном интеграле.

 . t
. t где
где  – непрерывно дифференцируемые функции параметра
– непрерывно дифференцируемые функции параметра  . (1.8)
. (1.8) , где
, где 
 .
.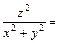
 . Вычислим производные функций:
. Вычислим производные функций: 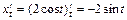 ,
, 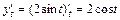 ,
,  и найдем дифференциал дуги:
и найдем дифференциал дуги: . Таким образом, получим:
. Таким образом, получим:  .
. . t
. t можно избавиться от корня следующим образом. Воспользуемся тригонометрической формулой понижения степени для косинуса:
можно избавиться от корня следующим образом. Воспользуемся тригонометрической формулой понижения степени для косинуса:  , тогда
, тогда  . Таким образом,
. Таким образом,  . Аналогично поступают с выражением
. Аналогично поступают с выражением  , используя тригонометрическую формулу понижения степени для синуса:
, используя тригонометрическую формулу понижения степени для синуса:  .
. проводят следующие преобразования:
проводят следующие преобразования:

 .
. , где
, где  (
( ) и
) и 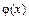 – непрерывно дифференцируемая функция на отрезке
– непрерывно дифференцируемая функция на отрезке  , причем
, причем  и
и  – абсциссы точек
– абсциссы точек  . (1.9)
. (1.9) задают пространственную кривую
задают пространственную кривую  – непрерывно дифференцируемые функции на отрезке
– непрерывно дифференцируемые функции на отрезке  . (1.10)
. (1.10) , где
, где  , заключенный между точками
, заключенный между точками  и
и 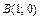 .
. заменим
заменим  :
: 
 . Так как
. Так как  , то
, то  . Так как абсцисса точки
. Так как абсцисса точки  , а абсцисса точки
, а абсцисса точки  . Таким образом, по формуле (1.9) вычисление данного криволинейного интеграла сведено к решению определенного интеграла. Получим:
. Таким образом, по формуле (1.9) вычисление данного криволинейного интеграла сведено к решению определенного интеграла. Получим:

 . t
. t , которая называется полюсом; лучом
, которая называется полюсом; лучом 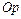 , который называется полярной осью и изображается горизонтально, а положительное направление определяется слева направо; единичным масштабом. Положение произвольной точки
, который называется полярной осью и изображается горизонтально, а положительное направление определяется слева направо; единичным масштабом. Положение произвольной точки 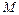 в полярных координатах определяется парой чисел:
в полярных координатах определяется парой чисел:  – расстояние от полюса до нее и
– расстояние от полюса до нее и  – угол, образованный отрезком
– угол, образованный отрезком  с полярной осью (положительное направление – против часовой стрелки) (рис. 1.3).
с полярной осью (положительное направление – против часовой стрелки) (рис. 1.3).
 ,
,  (1.11). Легко видеть, что
(1.11). Легко видеть, что  .
. , где
, где  (
( – непрерывно дифференцируемая функция на отрезке
– непрерывно дифференцируемая функция на отрезке  соответствует началу кривой
соответствует началу кривой 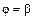 – концу кривой, тогда криволинейный интеграл I рода равен:
– концу кривой, тогда криволинейный интеграл I рода равен: . (1.12)
. (1.12) и расставляют пределы интегрирования
и расставляют пределы интегрирования 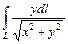 , где
, где  ,
,  .
.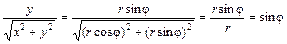 .
. , то
, то 
 . Пределы интегрирования в определенном интеграле известны по условию.
. Пределы интегрирования в определенном интеграле известны по условию.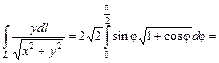
 .
. . t
. t , где
, где 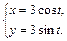
 , где
, где 
 ,
,  заключенная между точками
заключенная между точками  и
и  .
. , где
, где 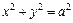 .
. , если
, если  (
( , если
, если 
 .
. , где
, где 
 , где
, где  , заключенный между точками
, заключенный между точками  .
. , где
, где  и
и  .
. , если
, если 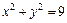 , лежащая в первом квадранте.
, лежащая в первом квадранте. между точками
между точками  .
. , если
, если  ,
,  и
и  .
. , где
, где  .
. , где
, где  , расположенной в первой координатной четверти.
, расположенной в первой координатной четверти. от
от  до
до 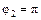 .
. , где
, где  ,
,  , заключенная внутри круга радиуса
, заключенная внутри круга радиуса  с центром в полюсе.
с центром в полюсе.


