
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление криволинейного интеграла II родаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Криволинейные интегралы II рода вычисляют, сводя к определенным интегралам. Параметрическое задание кривой интегрирования Если кривая ниями
Складывая почленно равенства (2.7) и (2.8), получим формулу для вычисления криволинейного интеграла II рода общего вида:
Пример 1. Вычислить w Решение. Воспользуемся формулой (2.9). При параметрическом построении окружности положительным направлением обхода является движение против часовой стрелки, поэтому параметр
= Ответ: Если кривая
Замечание. Применение формулы (2.10) при решении задач аналогично использованию формулы (2.9). Пример 2. Вычислить w Решение. Запишем параметрические уравнения прямой
Ответ: Явное задание кривой Если кривая
и
Криволинейный интеграл II рода общего вида по плоской кривой интегрирования
Пример 3. Вычислить w Решение. Так как дуга параболы расположена в первой координатной четверти, то
Ответ: Замечания 1. Если кривая
2. При неявном задании кривой Отметим важные частные случаи. Если кривая интегрирования
Аналогично, если кривая
Рис. 2.3 Если гладкая пространственная кривая
Замечание. Формулы (2.11) – (2.13), (2.17) получаются из формул (2.7) – (2.10) соответственно, если в качестве параметра взять Криволинейные интегралы I и II рода связаны равенством:
где
Рис. 2.4
Самостоятельная работа 1. Вычислить 2. Вычислить 3. Вычислить 4. Вычислить 5. Вычислить 6. Вычислить 7. Вычислить 8. Вычислить 9. Вычислить 10. Вычислить 11. Вычислить 12. Вычислить 13. Вычислить
|
||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.12.133 (0.011 с.) |

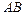
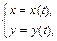
 , где функции
, где функции 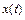 и
и  непрерывны вместе со своими производными на отрезке
непрерывны вместе со своими производными на отрезке 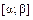 , причем начальной точке
, причем начальной точке  кривой соответствует значение параметра
кривой соответствует значение параметра 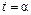 , а конечной точке
, а конечной точке 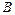 – значение
– значение 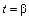 и пусть функции
и пусть функции 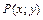 и
и  непрерывны на кривой
непрерывны на кривой 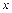 и
и 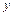 соответственно:
соответственно: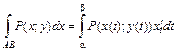 ; (2.7)
; (2.7)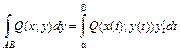 . (2.8)
. (2.8)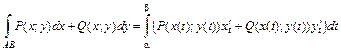 . (2.9)
. (2.9)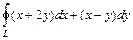 , где
, где  – окружность
– окружность 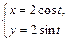 при положительном направлении обхода.
при положительном направлении обхода.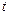 меняется от 0 до
меняется от 0 до 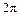 . Выполним необходимые преобразования:
. Выполним необходимые преобразования:  ,
, 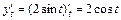 . Получим:
. Получим: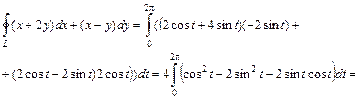
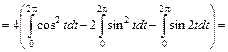
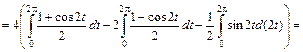 =
= 
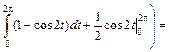 =
= 
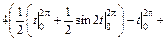
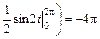 .
.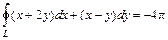 . t
. t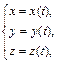
 непрерывны вместе со своими производными на отрезке
непрерывны вместе со своими производными на отрезке  ,
, 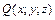 и
и  непрерывны на кривой
непрерывны на кривой 
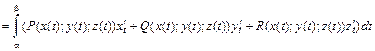 (2.10)
(2.10)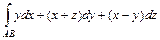 , где
, где 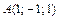 и
и 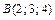 .
.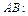
 Подставляя в уравнение
Подставляя в уравнение  абсциссы точек
абсциссы точек 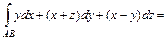

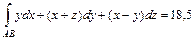 . t
. t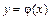 ,
, 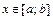 , где функция
, где функция 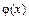 и ее производная
и ее производная  непрерывны на отрезке
непрерывны на отрезке 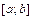 и функции
и функции  (2.11)
(2.11) . (2.12)
. (2.12)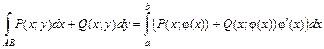 . (2.13)
. (2.13) , где
, где  – дуга параболы
– дуга параболы  от точки
от точки  до точки
до точки  .
.
 . Пределы интегрирования известны по условию, тогда по формуле (2.13) получим:
. Пределы интегрирования известны по условию, тогда по формуле (2.13) получим: 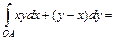

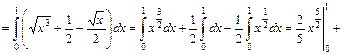
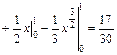 .
. . t
. t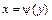 , то формула (2.13) примет вид:
, то формула (2.13) примет вид: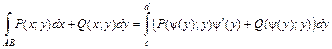 . (2.14).
. (2.14).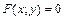 вычисление проводится по тем же формулам.
вычисление проводится по тем же формулам.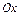 (рис.2.3, а), то криволинейный интеграл II рода сразу превращается в определенный, так как в этом случае
(рис.2.3, а), то криволинейный интеграл II рода сразу превращается в определенный, так как в этом случае 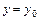 и
и 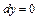 , поэтому
, поэтому . (2.15)
. (2.15)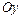 (рис. 2.3, б), то
(рис. 2.3, б), то 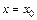 ,
,  и
и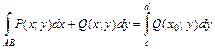 . (2.16)
. (2.16)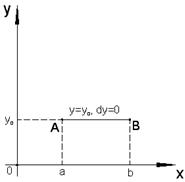

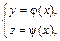
 и их производные
и их производные  непрерывны на отрезке
непрерывны на отрезке 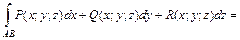
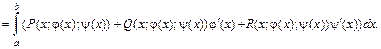 (2.17)
(2.17)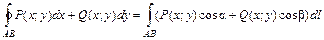 , (2.18)
, (2.18)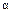 и
и 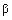 – углы, составляемые с осями координат направленной касательной к кривой
– углы, составляемые с осями координат направленной касательной к кривой  и положительное направление касательной соответствует направлению движения точки
и положительное направление касательной соответствует направлению движения точки 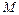 по кривой от
по кривой от 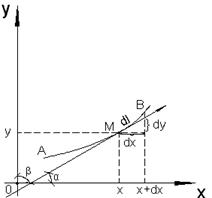
 , где
, где 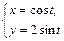 от точки
от точки 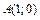 до точки
до точки 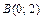 .
. , где
, где 
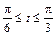 .
.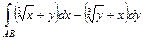 , где
, где 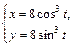 от точки
от точки  до точки
до точки 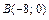 .
.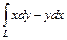 по петле листа Декарта
по петле листа Декарта 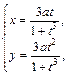
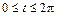 .
. , где
, где 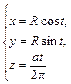 от точки пересечения линии с плоскостью
от точки пересечения линии с плоскостью 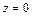 до точки ее пересечения с плоскостью
до точки ее пересечения с плоскостью 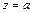 .
.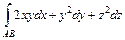 , где
, где 
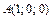 ,
,  .
. , где
, где  (
( ).
). , если
, если 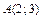 и
и 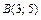 .
.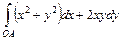 , где
, где 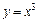 от точки
от точки  , если
, если  , где
, где 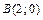 ,
, 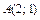 .
. , где
, где 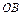 – отрезок прямой от точки
– отрезок прямой от точки 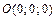 до точки
до точки 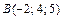 .
.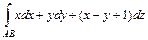 , где
, где 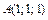 до точки
до точки  .
.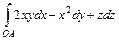 , где
, где 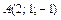 .
.


