
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые кривые на плоскостиСодержание книги Поиск на нашем сайте
1. Кубическая парабола: 2. Дробная функция: 3. Кубическая парабола: 4. Полукубическая парабола: 5. Парабола Нейля:
6. Локон Аньези: 7. Циклоида: 8. Циссоида Диоклеса:
9. Строфоида: 10. Гипоциклоида (астроида):
11. Эпициклоида:
Рис. 11 12. Кардиоида: 13. Лист Декарта:
14. Лемниската Бернулли: 15. Кривая Штейнера:
16. Трактриса: 17. Эвольвента (развертка) окружности:
18. Спираль Архимеда: 19. Гиперболическая спираль:
20. Логарифмическая спираль: 21. Трехлепестковая роза:
22. Четырехлепестковая роза: 23. Кривая каппа:
24. Конхоида Никомеда:
Рис. 24 25. «Жезл»:
26. Улитка:
27. Фигуры Лиссажу:
Рис. 27 28. Овал Кассини: 29. Кривая Ламе:
Приложение 2
КРИВЫЕ ВТОРОГО ПОРЯДКА 1. Каноническое уравнение окружности с центром в точке
Рис. 1
2. Парабола:
Рис. 2 3. Каноническое уравнение эллипса:
Рис. 3 4. Каноническое уравнение гиперболы:
Рис. 4
Приложение 3 Некоторые пространственные кривые 1. Винтовая линия: 2. Кривая Вивиани:
Приложение 4 Поверхности второго порядка 1. Каноническое уравнение эллиптического цилиндра: 2. Каноническое уравнение гиперболического цилиндра:
Рис. 1 Рис. 2
3. Каноническое уравнение параболического цилиндра: 4. Каноническое уравнение конуса второго порядка:
Рис. 3 Рис. 4 5. Каноническое уравнение эллипсоида: 6. Каноническое уравнение однополостного гиперболоида:
7. Каноническое уравнение двуполостного гиперболоида:
8. Каноническое уравнение эллиптического параболоида
9. Каноническое уравнение гиперболического параболоида:
Содержание
План уч.-метод. докум. 2008 г., поз. № 27
Составители: Е. В. Абрамов, Е. Д. Илларионова ПРЯМОЛИНЕЙНО О КРИВОЛИНЕЙНЫХ Методические указания для студентов очной и заочной форм обучения по дисциплине «Высшая математика»
Технический редактор Т. А. Скибина
Подписано в печать 18.05.2008 г. Формат 60 х 84 / 16. Гарнитура Times New Roman. Бумага UNION PRINTS. Печать трафаретная. Усл. печ. л. 3,55. Уч.-изд. л. 3,81. Т. 100 экз.
Волжский институт строительства и технологий (филиал) Волгоградского государственного архитектурно-строительного университета 404111 г. Волжский, пр. Ленина, 72
[1] В каждой точке существует касательная к данной кривой, и положение ее непрерывно меняется при перемещении этой точки по данной кривой [2] Область называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит (область без «дыр»)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.135.24 (0.01 с.) |

 (рис. 1).
(рис. 1). (рис. 2).
(рис. 2). (рис. 3).
(рис. 3). или
или  (рис. 4).
(рис. 4). или
или 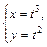 (рис. 5).
(рис. 5).


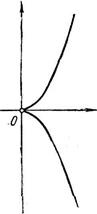

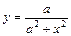 (рис. 6).
(рис. 6). где
где  (рис. 7).
(рис. 7).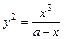 или
или  (рис. 8).
(рис. 8).
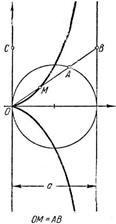

 или
или  (рис. 9).
(рис. 9).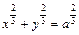 или
или  где
где 

 где
где 



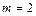
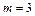
 (рис. 12).
(рис. 12). или
или  где
где 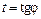 или
или  (рис. 13).
(рис. 13).

 или
или  (рис. 14).
(рис. 14). (рис. 15).
(рис. 15).

 (рис. 16).
(рис. 16). (рис. 17).
(рис. 17).

 , где
, где  (рис. 18).
(рис. 18). , где
, где  (рис. 19).
(рис. 19).

 (рис. 20).
(рис. 20). , где
, где 
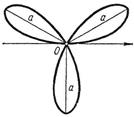
 (рис. 22).
(рис. 22). (рис. 23).
(рис. 23).

 (рис. 24, а – б).
(рис. 24, а – б).

 ,
, 

 (рис. 25).
(рис. 25). Рис. 25
Рис. 25
 (рис. 26, а – б).
(рис. 26, а – б).



 (рис. 27, а),
(рис. 27, а),  (рис. 27, б),
(рис. 27, б),  (рис. 27, в).
(рис. 27, в).

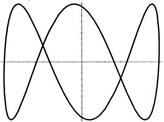
 , где
, где  ,
,  (рис. 28).
(рис. 28). (рис. 29).
(рис. 29).

 ,
, 
 ,
,

 и радиуса
и радиуса  :
:  (рис. 1).
(рис. 1).
 (рис. 2).
(рис. 2).
 (рис. 3).
(рис. 3).
 (рис. 4).
(рис. 4).
 (рис. 1).
(рис. 1). (рис. 2).
(рис. 2).



 (рис. 1). Если
(рис. 1). Если  , то
, то  – прямой круговой цилиндр.
– прямой круговой цилиндр. (рис. 2).
(рис. 2).
 (рис. 3).
(рис. 3). (рис. 4). Если
(рис. 4). Если  – прямой круговой конус.
– прямой круговой конус.
 (рис. 5). Если
(рис. 5). Если  , то
, то  – сфера.
– сфера.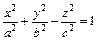 (рис. 6). Если
(рис. 6). Если  – однополостный гиперболоид вращения.
– однополостный гиперболоид вращения.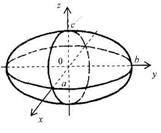 Рис. 5
Рис. 5
 Рис. 6
Рис. 6
 (рис. 7). Если
(рис. 7). Если  – двуполостный гиперболоид вращения.
– двуполостный гиперболоид вращения. (рис. 8). Если
(рис. 8). Если  , то
, то  – параболоид вращения.
– параболоид вращения. (рис. 9).
(рис. 9). Рис. 7
Рис. 7
 Рис. 8 Рис. 9
Рис. 8 Рис. 9



