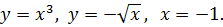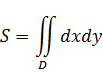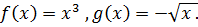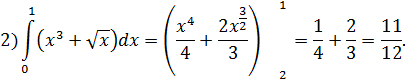Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения определенного интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Задача 9. Пользуясь однократным интегралом, вычислить площадь области, ограниченной линиями:
Решение. Начать следует с построения области, площадь которой требуется найти. 1)
Рис.1 Так как область интегрирования прилегает к оси О х, то для нахождения площади области следует воспользоваться формулой
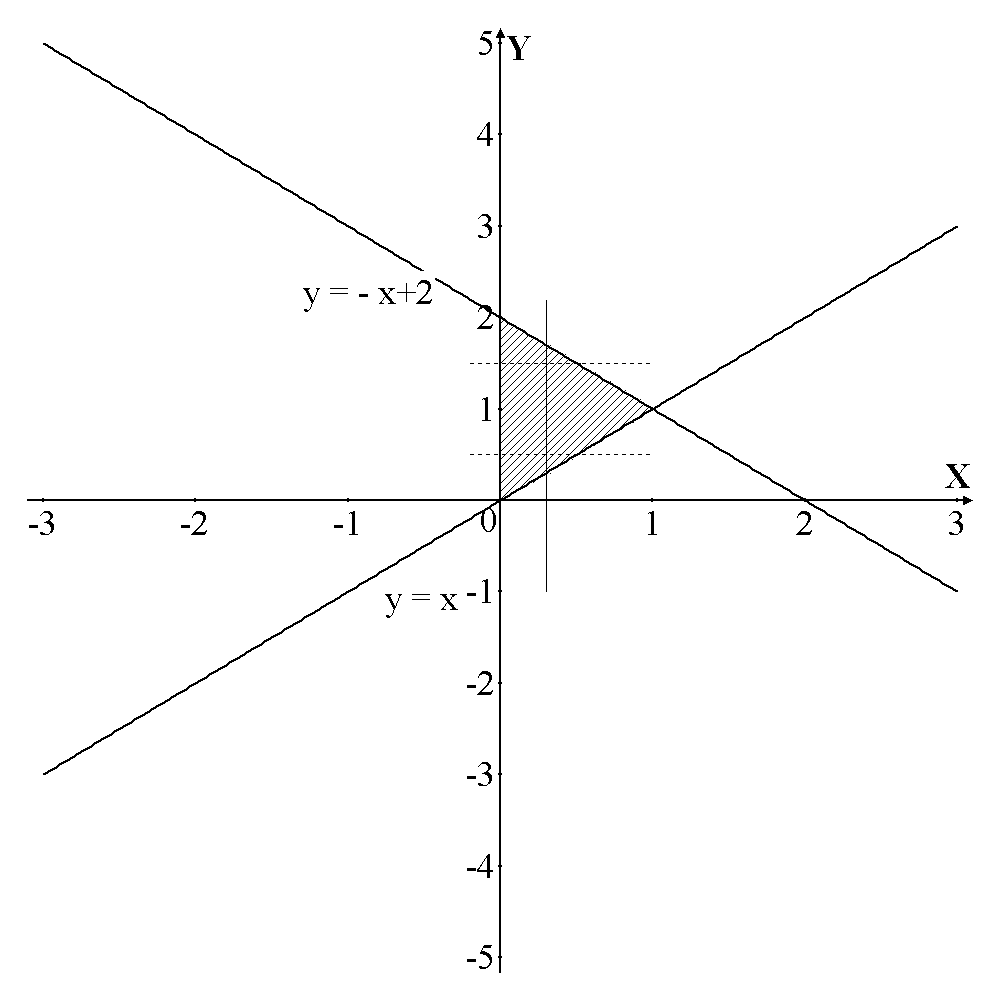
Рис.2 Так как область заключена между двумя линиями, то для нахождения её площади следует воспользоваться формулой
Задача 10. Решить задачу: 1) Скорость движения точки 2) При сжатии пружины на 0,05 м затрачивается работа 25 Дж. Какую работу необходимо совершить, чтобы сжать пружину на 0,1 м? Решение. 1) Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью t 1 до t 2, вычисляется по формуле Скорость точки равна нулю в момент начала движения и в момент остановки. Для нахождения момента остановки точки надо решить уравнение:
2) Работа, произведенная переменной силой Зная величину сжатия пружины (0,05 м) и произведенную при этом работу (25 Дж), воспользоваться формулой работы:
откуда
Кратные интегралы Повторный интеграл Задача 11. Вычислить повторный интеграл:
Решение. Сначала вычисляется внутренний интеграл, где у является переменной, а х постоянной:
Полученный результат подставить под знак внешнего интеграла и проинтегрировать его по переменной х.
Таким образом,
Двойной интеграл Задача 12. Привести двойной интеграл
по области D к повторному двумя способами и вычислить его. Решение. Вычисление двойного интеграла начинается с изображения области интегрирования. Все линии, ограничивающие область, необходимо построить и подписать (рис.3).
Рис. 3 Следующий шаг – переход от двойного интеграла к повторному. Для этого необходимо выбрать порядок интегрирования в повторном интеграле, т.е. Чтобы выбрать наиболее удобный для вычисления порядок интегрирования, надо посмотреть, относительно какой оси нет «узлов» (то есть точек стыка различных линий). В нашем случае относительно оси О х нет «узлов», поэтому в таком порядке как Для того чтобы найти внешние пределы интегрирования, нужно спроецировать крайние точки области на ось, дифференциал которой стоит под знаком внешнего интеграла. В нашем случае ─ на ось О х, т.к. имеет место
1) Сначала вычисляется внутренний интеграл, где y является переменной, а х постоянной:
2) Затем вычисляется внешний интеграл, подставив в него результат вычисления внутреннего интеграла.
При расстановке пределов вторым способом получается следующий результат
Геометрические приложения двойного интеграла Задача 13. Пользуясь двойным интегралом, найти площадь плоской области D, ограниченной указанными линиями: Решение. Площадь с помощью двойного интеграла вычисляется по формуле
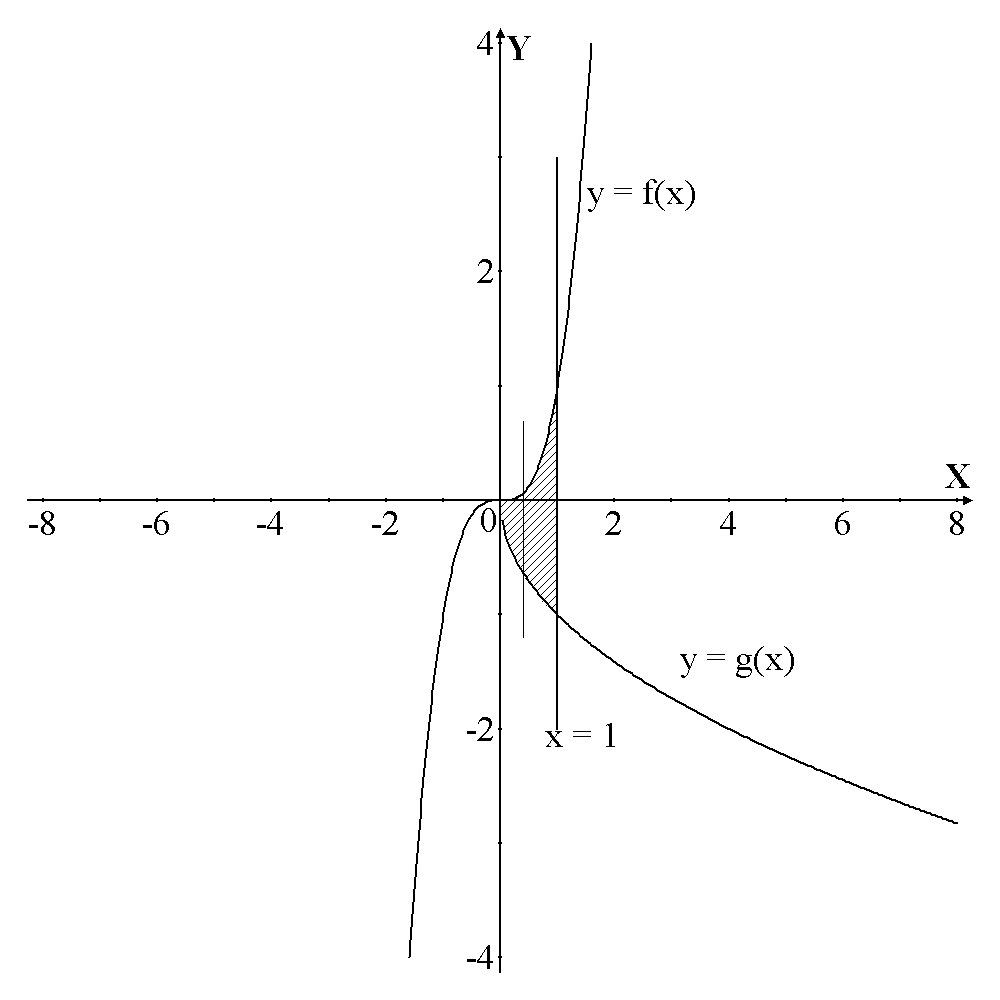
Начать следует с изображения области, площадь которой требуется найти. На рис.4
Рис. 4
Криволинейный интеграл
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

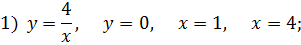
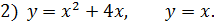
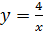 ‑ гипербола,
‑ гипербола, 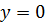 ‑ ось О х,
‑ ось О х, 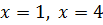 ‑ прямые параллельные оси О у (рис.1).
‑ прямые параллельные оси О у (рис.1).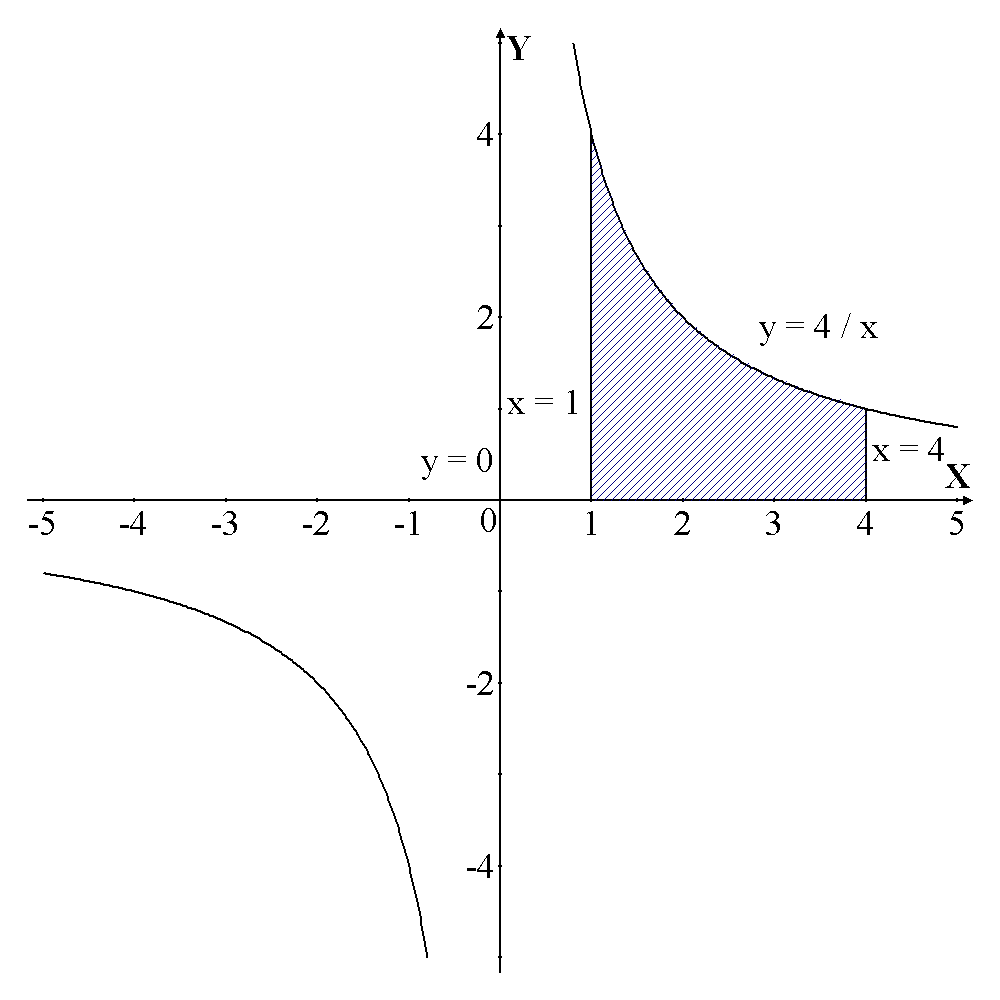
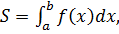 где
где 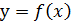 ‑ уравнение линии, ограничивающей область сверху. Тогда
‑ уравнение линии, ограничивающей область сверху. Тогда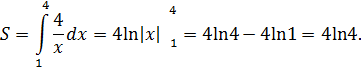
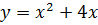 ‑ парабола, которая пересекает ось О х в точках
‑ парабола, которая пересекает ось О х в точках 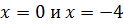 , и имеет вершину в точке
, и имеет вершину в точке 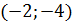 ,
, 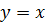 – прямая, являющаяся биссектрисой 1 и 3 координатных углов (рис.2).
– прямая, являющаяся биссектрисой 1 и 3 координатных углов (рис.2).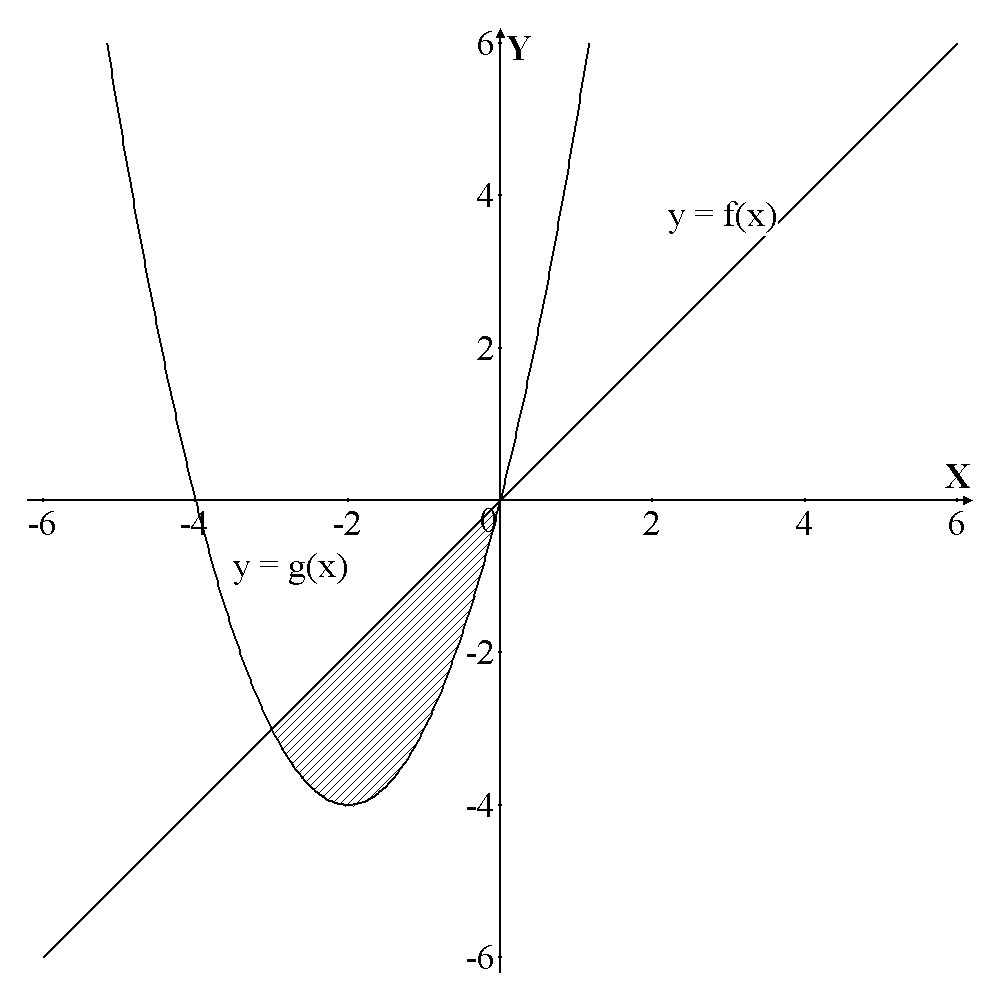
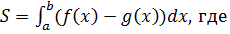
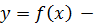 уравнение линии, ограничивающей область сверху, а
уравнение линии, ограничивающей область сверху, а 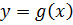 снизу. Для нахождения пределов интегрирования нужно найти абсциссы точек пересечения параболы и прямой, решив совместно эти уравнения.
снизу. Для нахождения пределов интегрирования нужно найти абсциссы точек пересечения параболы и прямой, решив совместно эти уравнения.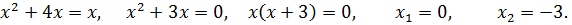
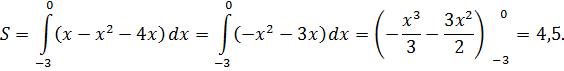
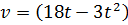 м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.
м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.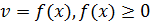 за промежуток времени от
за промежуток времени от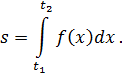
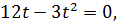 откуда
откуда 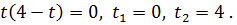 Тогда
Тогда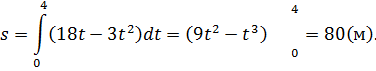
 при перемещении по оси
при перемещении по оси 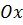 материальной точки от
материальной точки от 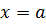 до
до 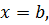 находится по формуле
находится по формуле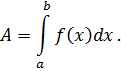
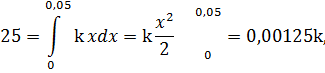
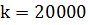 (Н/м). Теперь по этой же формуле найти:
(Н/м). Теперь по этой же формуле найти: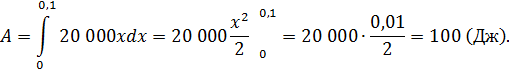





 или
или  .
.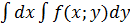 будет один повторный интеграл.
будет один повторный интеграл.
 , выход на линии
, выход на линии  ). Таким образом,
). Таким образом,