
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неопределенный интеграл и методы его вычисленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Неопределенный интеграл и методы его вычисления
Основные свойства неопределённого интеграла и правила интегрирования Для решения задачи нахождения по заданной производной Дифференцируемая на некотором промежутке
Теорема. Если функция Доказательство. 1) Так как
то при любом выборе постоянной С функция 2) Пусть
Рассмотрим функцию
Имеем:
на множестве Х. В силу теоремы Лагранжа о конечных приращениях функция
Неопределенным интегралом от непрерывной функции Обозначается:
Обычно фигурные скобки в правой части опускают и записывают (1.6) в виде:
считая С произвольной постоянной. Функция
- подынтегральным выражением. Знак Из (1.7) непосредственно следует:
Теорема. Справедливы следующие правила интегрирования функций:
Доказательство. Дифференцируя левые и правые части этих равенств с учетом формул (1.9), приходим к одинаковому результату. Действительно, 1) 2) 3) 4)
Правило (1.12) называется правилом «замены переменных», правило (1.13) называется правилом «интегрирования по частям».
Таблица основных формул интегрирования
Таблица неопределенных интегралов
Для доказательства правильности формул таблицы достаточно продифференцировать обе её части с использованием свойств неопределённого интеграла и формул дифференцирования и убедится в совпадении результатов.
Рассмотрим несколько примеров. №1.
№2.
№3.
№4. №5.
№6.
№7.
№8.
№9.
Вычисляем
Получаем:
Следовательно,
№10.
Определённый интеграл. Формула Ньютона-Лейбница Замена переменных в определённом интеграле
Пусть дан интеграл Введем новую переменную в соответствии с формулой 1) 2) функции 3) функция
Тогда Пример.
При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду. Пример.
т. е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная
Интегрирование по частям определённого интеграла
Если функции
Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше.
Формула прямоугольников
Если известны значения функции
Разобьем отрезок интегрирования на
Составим суммы
любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.
Формула трапеций
Эта формула является более точной по сравнению с формулой прямоугольников. Подынтегральная функция в этом случае заменяется на вписанную ломаную.
a Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Очевидно, что чем больше взять точек Площади вписанных трапеций вычисляются по формулам:
После приведения подобных слагаемых получаем формулу трапеций:
Формула парабол (формула Симпсона или квадратурная формула).
Разделим отрезок интегрирования
0
Уравнения этих парабол имеют вид
Обозначим
Если принять Тогда уравнения значений функции (6.1) имеют вид:
C учетом этого: Отсюда уравнение (6.2) примет вид: Тогда
Складывая эти выражения, получаем формулу Симпсона:
Чем больше взять число
Пример. Вычислить приближенное значение определенного интеграла
Точное значение этого интеграла – 91.173. Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная. Для сравнения применим к этой же задаче формулу трапеций.
Кроме вышеперечисленных способов, можно вычислить значение определенного интеграла с помощью разложения подынтегральной функции в степенной ряд. Принцип этого метода состоит в том, чтобы заменить подынтегральную функцию по формуле Тейлора и почленно проинтегрировать полученную сумму. Пример. С точностью до 0,001 вычислить интеграл
Так как интегрирование производится в окрестности точки Разложение функции
Зная разложение функции
Теперь представим в виде ряда подынтегральное выражение:
Теперь представим наш интеграл в виде:
Применим теорему о почленном интегрировании ряда. (Т.е. интеграл от суммы будет представлен в виде суммы интегралов членов ряда). Вообще говоря, со строго теоретической точки зрения для применения этой теоремы надо доказать, что ряд сходится равномерно на отрезке интегрирования Таким образом
Получаем:
Как видно, абсолютная величина членов ряда очень быстро уменьшается, и требуемая точность достигается уже при третьем члене разложения. Более точное значение этого интеграла: 0,2482725418… Пример.
Несобственный интеграл расходится. Пример.
Неопределенный интеграл и методы его вычисления
Основные свойства неопределённого интеграла и правила интегрирования Для решения задачи нахождения по заданной производной Дифференцируемая на некотором промежутке
Теорема. Если функция Доказательство. 1) Так как
то при любом выборе постоянной С функция 2) Пусть
Рассмотрим функцию
Имеем:
на множестве Х. В силу теоремы Лагранжа о конечных приращениях функция
Неопределенным интегралом от непрерывной функции Обозначается:
Обычно фигурные скобки в правой части опускают и записывают (1.6) в виде:
считая С произвольной постоянной. Функция
- подынтегральным выражением. Знак Из (1.7) непосредственно следует:
Теорема. Справедливы следующие правила интегрирования функций:
Доказательство. Дифференцируя левые и правые части этих равенств с учетом формул (1.9), приходим к одинаковому результату. Действительно, 1) 2) 3) 4)
Правило (1.12) называется правилом «замены переменных», правило (1.13) называется правилом «интегрирования по частям».
Таблица основных формул интегрирования
Таблица неопределенных интегралов
Для доказательства правильности формул таблицы достаточно продифференцировать обе её части с использованием свойств неопределённого интеграла и формул дифференцирования и убедится в совпадении результатов.
Рассмотрим несколько примеров. №1.
№2.
№3.
№4. №5.
№6.
№7.
№8.
№9.
Вычисляем
Получаем:
Следовательно,
№10.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.253.240 (0.012 с.) |

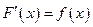 самой функции
самой функции 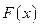 служит операция интегрирования функций, являющаяся обратной по отношению к операции дифференцирования.
служит операция интегрирования функций, являющаяся обратной по отношению к операции дифференцирования.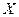 функция
функция 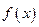 , определенной на том же промежутке, если для каждого числа
, определенной на том же промежутке, если для каждого числа  выполняется равенство:
выполняется равенство: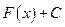 , где С - произвольная постоянная.
, где С - произвольная постоянная. , (1.2)
, (1.2)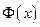 - произвольная первообразная для функции
- произвольная первообразная для функции  ,
,  . (1.4)
. (1.4)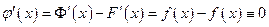
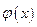 является постоянной:
является постоянной:  . Следовательно,
. Следовательно,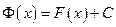 . (1.5)
. (1.5)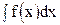 . Читается: «интеграл
. Читается: «интеграл 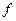 от икс дэ икс». По определению
от икс дэ икс». По определению ,
, 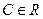 . (1.6)
. (1.6)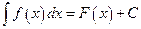 , (1.7)
, (1.7)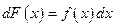 (1.8)
(1.8) называется знаком неопределенного интеграла, а переменная
называется знаком неопределенного интеграла, а переменная 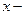 переменной интегрирования.
переменной интегрирования.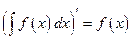 ,
, 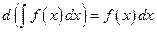 ,
, 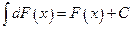 . (1.9)
. (1.9)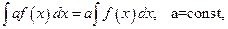 (1.10)
(1.10)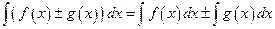 , (1.11)
, (1.11)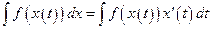 , (1.12)
, (1.12) . (1.13)
. (1.13)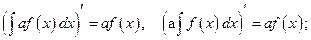
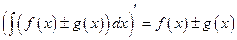 ,
, 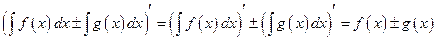 ;
;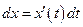 ,
,  ;
;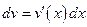 ,
, 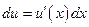 ,
,  ,
, .
.
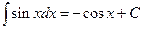

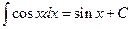
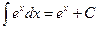
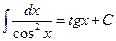
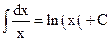

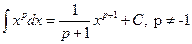

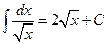
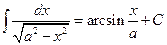
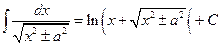
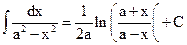
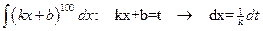
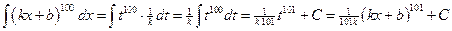 .
.
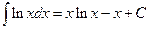 .
.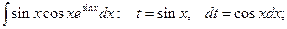

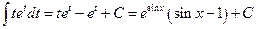 .
.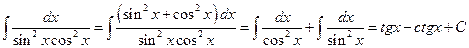 .
.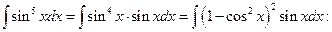
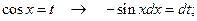

 .
.
 .
.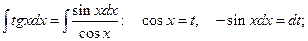
 .
.
 .
.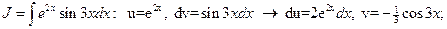
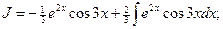
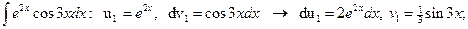
 .
.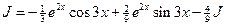 .
.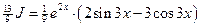 , т.е.
, т.е. 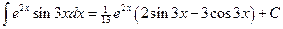 .
.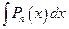 , где
, где 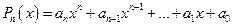 - многочлен степени
- многочлен степени 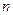 с действительными коэффициентами
с действительными коэффициентами 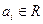
 . Используя правила (1.10), (1.11) и таблицу (1.14), находим:
. Используя правила (1.10), (1.11) и таблицу (1.14), находим: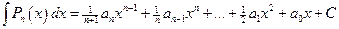 . (2.1)
. (2.1)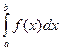 , где
, где 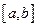 .
.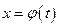 . Тогда если
. Тогда если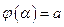 ,
, 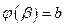
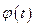 и
и 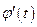 непрерывны на отрезке
непрерывны на отрезке 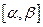
 определена на отрезке
определена на отрезке  .
.
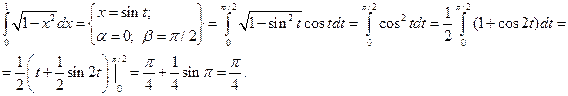
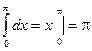 , с другой стороны, если применить тригонометрическую подстановку,
, с другой стороны, если применить тригонометрическую подстановку,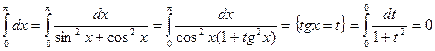 ,
, имеет на отрезке интегрирования разрыв (в точке
имеет на отрезке интегрирования разрыв (в точке 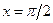 ). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.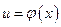 и
и  непрерывны на отрезке
непрерывны на отрезке 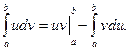
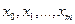 , то в качестве функции аппроксимирующей
, то в качестве функции аппроксимирующей 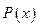 степени не выше
степени не выше 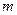 , значения которого в выбранных точках равны значениям функции f(x) в этих точках.
, значения которого в выбранных точках равны значениям функции f(x) в этих точках.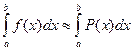 .
.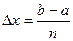 . При этом:
. При этом: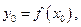
 , ….,
, ….,  .
. ;
;  - соответственно нижнюю и верхнюю интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной. Тогда
- соответственно нижнюю и верхнюю интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной. Тогда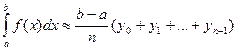 или
или  -
- y
y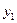
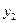
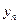
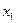
 b x
b x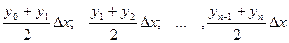 ;
; .
.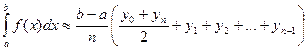
 . Площадь криволинейной трапеции, ограниченной графиком функции
. Площадь криволинейной трапеции, ограниченной графиком функции 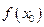 ,
, 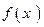 ,
, 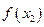 . Для каждой пары отрезков построим такую параболу.
. Для каждой пары отрезков построим такую параболу.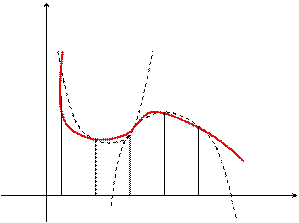
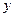
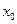
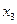
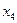 х
х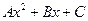 , где коэффициенты
, где коэффициенты 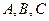 могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
могут быть легко найдены по трем точкам пересечения параболы с исходной кривой. (6.1)
(6.1) .
.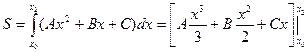 .
.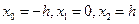 , то
, то 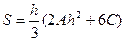 (6.2)
(6.2)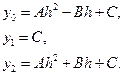
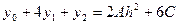 .
.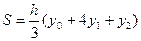 .
.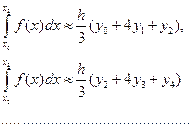
 .
.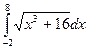 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим: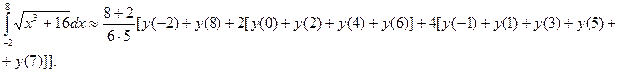
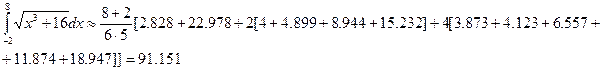
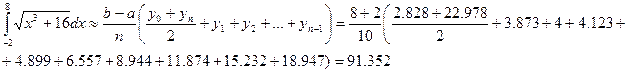 Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.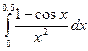 .
.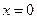 , то можно воспользоваться для разложения подынтегральной функции формулой Маклорена.
, то можно воспользоваться для разложения подынтегральной функции формулой Маклорена.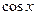 имеет вид:
имеет вид: .
.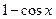 :
: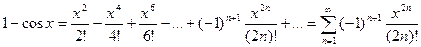 .
.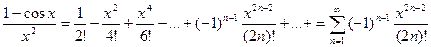 .
. .
.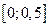 .
.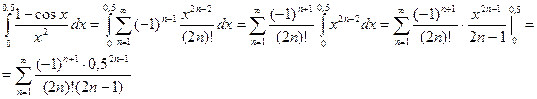
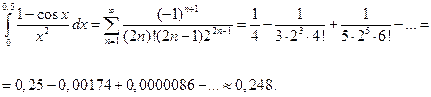
 - не существует.
- не существует. - интеграл сходится
- интеграл сходится


