
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 6. Неопределенный интеграл.Содержание книги
Поиск на нашем сайте
Содержание модуля. Тема 6. 1. Первообразная. Неопределенный интеграл, его свойства. Таблица основных интегралов. Интегрирование заменой переменной и по частям. Тема 6. 2. Интегрирование рациональных дробей. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных выражений. Методические указания по его изучению. После изучения по учебникам теоретического материала разберите реше- ние примеров 11 - 13. Для справок приведем следующую таблицу основных неопределенных интегралов. (I) (II) (III) (IV) (V) (VI) (VII) (VIII) (IX) (X) (XI) (XII) (XIII ) где F (x) – первообразная для f (x).
Пример 11. Вычислить неопределенные интегралы: а) Решение. а) Чтобы данный интеграл привести к табличному, положим Имеем
б) Для вычисления интеграла введем подстановку sinx = t. Имеем cosxdx = dt. Тогда
в) Под знаком интеграла имеем неправильную рациональную дробь (числитель – многочлен пятой степени, знаменатель – второй). Разделив многочлен
Тогда
Правильную рациональную дробь дующей суммы элементарных дробей:
После приведения в последнем равенстве к общему знаменателю получаем тождество
Имеем Следовательно,
Пример 12. Вычислить интегралы: а) Решение. а)Выделяем в знаменателе дроби полный квадрат и применяем формулу (ХI).
=
б) Выделим в числителе дроби производную ее знаменателя, то есть выражение 4 х – 5, преобразуем дробь, применяем формулы (II) и (ХI).
= + = в) Выделим в числителе дроби производную трехчлена
=
Пример 13. Вычислить интегралы: а) Решение. Применяем формулу интегрирования по частям: а) Положим По формуле интегрирования по частям получаем:
= б) Пусть u =x 2, dv = sinxdx, тогда du = 2 xdx, По приведенной выше формуле имеем:
Последний интеграл вычислим этим же способом, положив u = x, dv = cosxdx, откуда du = dx, v = sinx. Тогда
Имеем
Вопросы для самоконтроля. 1. Сформулируйте определение первообразной функции. 2. Что называется неопределенным интегралом от данной функции?
3. Каков геометрический смысл неопределенного интеграла? 4. Перечислите свойства неопределенного интеграла. 5. Напишите формулы таблицы основных интегралов. 6. В чем сущность метода замены переменной при вычислении неопределенных интегралов? 7. Напишите формулу интегрирования по частям в неопределенном интеграле. 8. Укажите типы интегралов, вычисление которых целесообразно производить при помощи метода интегрирования по частям. 9. Изложите правило разложения правильной рациональной дроби на сумму простейших дробей. 10. Изложите методы интегрирования простейших рациональных дробей.
2. 6. 4. Задания для самостоятельной работы Вычислить неопределенные интегралы. 1. 4. 7.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.250.57 (0.009 с.) |

 , где n ≠ - 1.
, где n ≠ - 1. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. ,
, ; б)
; б) 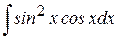 ; в)
; в)  .
. . Тогда
. Тогда  и
и  .
. .
. .
. на
на  , в частном получим
, в частном получим и в остатке
и в остатке  .
. .
. представим в виде сле-
представим в виде сле- .
. ;
;  .
. , отсюда
, отсюда  ,
,  .
. и
и
 .
. ; б)
; б)  ; в)
; в)  .
. =
=  =
= =
=  =
=  .
.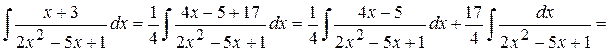
 =
=  +
+ =
= 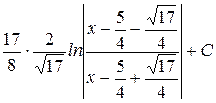 =
= .
. , то есть
, то есть  , преобразуем подынтегральную дробь, применяем формулы (I) и (IX).
, преобразуем подынтегральную дробь, применяем формулы (I) и (IX).

 =
= 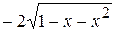 –
– + С =
+ С =  + С.
+ С. ; б)
; б)  .
. .
. . Тогда
. Тогда  .
. =
=
 .
. .
. .
. .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5. 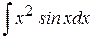 . 8.
. 8.  . 9.
. 9. 



