
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 7. Определенный интеграл.
Содержание модуля. Тема 7. 1.Задачи, приводящие к понятию определенного интеграла. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов. Методы вычисления определенного интеграла по формулам прямоугольников, трапеций, Симпсона. Несобственные интегралы с бесконечными пределами и от неограниченных функций, их основные свойства. Тема 7. 2. Приложение определенного интеграла.
Методические указания по его изучению. После изучения по учебникам теоретического материала разберите реше- ние примеров 13 - 16. Пример 13. Вычислить площадь фигуры, ограниченной линиями Решение. Найдем абсциссы точек пересечения данной параболы и прямой (рис. 5):

Рис. 5
Пример 14. Вычислить объем тела, образованного вращением вокруг оси Ох одной полуволны синусоиды y = sinx. Решение. Если криволинейная трапеция,ограниченная сверху кри- вой
Имеем:
Пример15. Найти площадь поверхности эллипсоида, образованного вращением вокруг оси Ох эллипса Решение. Если непрерывная на отрезке
Из уравнения эллипса находим
Для вычисления последнего интеграла применим подстановку
Тогда
Пример 16. Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями Решение. Координаты центра тяжести x = b и осью Ох, определяются по формулам
где S – площадь криволинейной трапеции. Данная фигура (рис. 6) симметрична относительно оси Ох.

Рис. 6
Итак, точка
Вопросы для самоконтроля. 1. Назовите задачи, приводящие к понятию определенного интеграла. 2. Напишите интегральную сумму для функции
3. Что называется определенным интегралом от функции 4. Каков геометрический смысл определенного интеграла?
5. Перечислите свойства определенного интеграла. 6. Чему равна производная от определенного интеграла с переменным верхним пределом интегрирования? 7. Напишите формулу Ньютона – Лейбница. 8. Напишите формулу замены переменной в определенном интеграле. 9. Чему равен интеграл 10. Напишите формулу интегрирования по частям в определенном интеграле. 11. Сформулируйте определение несобственного интеграла с бесконечными пределами интегрирования. 12. Сформулируйте определение несобственного интеграла от разрывной функции. 13. В каком случае несобственный интеграл называется сходящимся? расходящимся? 14. Как вычисляется площадь плоской фигуры в прямоугольной системе координат с помощью определенного интеграла? 15. Напишите формулы для вычисления объемов тел, образованных вращением плоской фигуры вокруг оси Ох; оси Оу.
2. 7. 4. Задания для самостоятельной работы Вычислить определенные интегралы. 1. 4.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.29 (0.011 с.) |
 ,
, 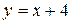 .
. ,
,  ,
,  ,
,  .
. =
= 
 .
.
 , прямыми х = а, x = b и осью Ох, вращается вокруг оси Ох, то объем V тела вращения равен
, прямыми х = а, x = b и осью Ох, вращается вокруг оси Ох, то объем V тела вращения равен .
. .
. .
. кривая
кривая  вращается вокруг оси Ох, то площадь S поверхности вращения вычисляется по формуле
вращается вокруг оси Ох, то площадь S поверхности вращения вычисляется по формуле . (1)
. (1) , откуда
, откуда  . По формуле (1) имеем
. По формуле (1) имеем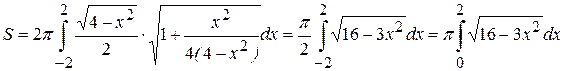 .
. , откуда
, откуда  . Если х = 0, то t = 0;
. Если х = 0, то t = 0;  при х = 2.
при х = 2.
 .
. , х = 4.
, х = 4.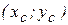 однородной криволинейной трапеции, ограниченной кривой
однородной криволинейной трапеции, ограниченной кривой  ; (1)
; (1)  (2),
(2), 
 .
Найдем площадь S фигуры:
.
Найдем площадь S фигуры:
 .
По формуле (1) имеем
.
По формуле (1) имеем
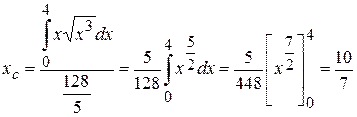
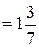 .
. − центр тяжести данной фигуры.
− центр тяжести данной фигуры. на отрезке
на отрезке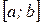 .
. на отрезке
на отрезке  ?
? , если
, если  . 2.
. 2.  . 3.
. 3. 
 . 5.
. 5.  . 6.
. 6.  .
.


