
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эксплуатация транспортно-технологических машин иСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ ЗАОЧНЫЙ УНИВЕРСИТЕТ» Факультет механизации и технического сервиса Кафедра высшей математики МАТЕМАТИКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ И ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ Студентам 1 и 2 курсов по направлениям подготовки бакалавров Агроинженерия» Профили: «Технический сервис в агропромышленном комплексе»; «Технические системы в агробизнесе»; «Технологическое оборудование для хранения и переработки с/х продукции»; «Электрооборудование и электротехнологии» Эксплуатация транспортно-технологических машин и Комплексов» Профиль: «Автомобильный сервис» Информационные системы и технологии» Профиль: «Информационные системы и технологии» Природообустройство и водопользование» Профили: «Комплексное использование и охрана водных ресурсов»; «Природоохранное обустройство территории»; «Инженерные системы сельскохозяйственного водоснабже - ния, обводнения и водоотведения»
Москва 2011 Составители: доценты Лычкин В.Н., Капитонова В.А.
УДК 517. (076)
Математика: Методические указания по изучению дисциплины/ Рос. гос. аграр. заоч. ун-т; Сост. Лычкин В.Н., Капитонова В.А. М., 2011. стр.
Предназначены для студентов 1, 1* и 2, 2* курсов
Утверждены методической комиссией факультета механизации и технического сервиса
Рецензенты:
Раздел 1. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ Дисциплина «Математика» относится к базовой (обязательной) части второго цикла ООП. Методические указания по данной дисциплине составлены в соответствии с требованиями Федерального государственного образовательного стандарта высшего профессионального образования, утвержденного Министерством образования и науки РФ 9 ноября 2009 г. по направлению подготовки «110800 – Агроинженерия», примерной программой по дисциплине и рабочими учебными планами, утвержденными ученым советом ФГОУ ВПО РГАЗУ 26 января 2011 г.
1. 1. Цели и задачи дисциплины
Целью математического образования является развитие навыков математического мышления; навыков использования математических методов и основ математического моделирования; математической культуры у обучающегося. Ему необходимо в достаточной степени владеть как классическими, так и современными математическими методами анализа задач, возникающих в его практической деятельности, использовать возможности вычислительной техники, уметь выбирать наиболее подходящие комбинации известных методов, знать их сравнительные характеристики. Для выработки у современных специалистов с высшим образованием необходимой математической культуры необходимо решение следующих задач: 1.Обеспечение высокого уровня фундаментальной математической подготовки студентов. 2. Выработки у студентов умения проводить логический и качественный анализ социально-экономических задач управления на основе построения математических моделей на базе различных средств информационного обеспечения. 3. Умение использовать методы современной математики, необходимые для работы по выбранной специальности. 4. Умение специалиста самостоятельно продолжить свое математическое образование. В результате изучения дисциплины студент должен: 1) обладать следующими общекультурными компетенциями (ОК): - владением культурой мышления, способностью к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения (ОК-1); - умением логически верно, аргументировано и ясно строить устную и письменную речь (ОК-2); 2) обладать следующими профессиональными компетенциями (ПК): - способностью к использованию основных законов естественнонаучных дисциплин в профессиональной деятельности, применением методов математического анализа и моделирования (ПК-1); - способностью решать инженерные задачи с использованием основных законов механики, электротехники, гидравлики, термодинамики (ПК-3); - способностью проводить и оценивать результаты измерений (ПК-5); - готовностью к обработке результатов экспериментальных исследований. В результате изучения дисциплины студент должен: знать основные понятия и методы математического анализа, линейной алгебры и аналитической геометрии, дискретной математики, теории дифференциальных уравнений, теории вероятностей и теории математической статистики, статистических методов обработки экспериментальных данных, элементов теории функций комплексной переменной; уметь использовать математический аппарат для обработки технической и экономической информации и анализа данных, связанных с машиноиспользо- ванием и надежностью технических систем; владеть методами построения математических моделей типовых профессиональных задач.
Библиографический список Основной 1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2002. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 2002. 3. Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, любое издание. 4. Кудрявцев В.А., Демидович В.П. Краткий курс высшей математики. М.: Наука, любое издание. 5. Минорский В.П. Сборник задач по высшей математике. М.: Наука, 2000. 6. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. 1, 2. М.: Наука, любое издание. Дополнительный 7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т. 1, 2. – М.: Высшая школа, 1996. 8. Лычкин В.Н. Высшая математика в задачах. Учебное пособие. М.: РГАЗУ, 2009. 9. Лычкин В.Н. Высшая математика. Учебное пособие. М.: РГАЗУ, 2011.
Раздел 2. СОДЕРЖАНИЕ УЧЕБНЫХ МОДУЛЕЙ ДИСЦИПЛИНЫ Содержание модуля. Те м а 1. 1. Аналитическая геометрия на плоскости. Уравнения линий на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой. Кривые второго порядка: окружность, эллипс, гипербола, парабола, Их геометрические свойства и уравнения. Технические приложения геометрических свойств кривых (использование фокальных свойств, математические модели формообразования технических и других объектов). Т е м а 1. 2. Элементы линейной алгебры. Определители второго и третьего порядков, их свойства. Алгебраические дополнения и миноры. Определители n-го порядка. Вычисление определителя его разложением по строке (столбцу). Системы двух и трех линейных уравнений. Матричная запись системы линейных уравнений. Правило Крамера. Система линейных уравнений с n неизвестными. Метод Гаусса. Матрицы, действия над ними. Обратная матрица. Т е м а 1. 3. Элементы векторной алгебры и аналитической геометрии в пространстве. Системы координат на прямой, плоскости и в пространстве. Пространства R 2 и R 3. Векторы. Линейные операции над векторами. Скалярное произведение векторов и его свойства. Длина вектора и угол между двумя векторами в координатной форме. Условие ортогональности двух векторов. Механический смысл скалярного произведения. Векторное произведение двух векторов, его свойства. Условие коллинеарности двух векторов. Геометрический смысл определителя 2-го порядка. Простейшие приложения векторного произведения в науке и технике. Смешанное произведение трех векторов. Его геометрический смысл. Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью. Уравнение поверхности в пространстве. Цилиндрические поверхности. Сфера. Конус. Эллипсоид. Гиперболоиды. Параболоиды. Геометрические свойства этих поверхностей, Исследование их формы методом сечений. Технические приложения геометрических свойств поверхностей (использование фокальных свойств, модели строительных конструкций, физические модели элементов и т.п.). Полярные координаты на плоскости. Цилиндрические и сферические координаты в пространстве.
Вопросы для самоконтроля. Те м а 1. 1. Аналитическая геометрия на плоскости. 1. Что называется прямоугольной системой координат на плоскости? 2. Чему равны ординаты точек, лежащих на оси Ох? 3. Чему равны абсциссы точек, лежащих на оси Оу? 4. Напишите формулу для вычисления расстояния между двумя точками на плоскости. 5. Напишите формулы для вычисления координат точки, делящей отрезок в данном отношении. 6. Напишите формулы для определения координат точки, делящей отрезок пополам. 7. Что называется уравнением линии на плоскости? 8. Напишите уравнение прямой с угловым коэффициентом. 9. Что называется угловым коэффициентом прямой, каков его геометрический смысл? 10. Чему равен угловой коэффициент прямой, параллельной оси Ох? 11. Напишите формулу для вычисления угла между двумя прямыми. 12. Сформулируйте условие параллельности двух прямых. 13. Сформулируйте условие перпендикулярности двух прямых. 14. Напишите уравнение прямой, проходящей через данную точку в данном направлении. 15. Напишите уравнение прямой, проходящей через две данные точки. 16. Напишите общее уравнение прямой. 17. Как найти угловой коэффициент прямой, если дано ее общее уравнение? 18. Как найти координаты точек пересечения двух прямых, если даны их уравнения? 19. Какие линии называются кривыми второго порядка? 20. Напишите уравнение окружности с центром в данной точке. 21. Напишите уравнение окружности с центром в начале координат. 22. Что называется эллипсом? Напишите каноническое уравнение эллипса. 23. Что называется эксцентриситетом эллипса? 24. Дайте определение гиперболы. Напишите каноническое уравнение гиперболы. 25. Что называется эксцентриситетом гиперболы? 26. Что называется асимптотой гиперболы? Напишите уравнения асимптот гиперболы. 27. Что называется параболой? Напишите каноническое уравнение параболы, симметричной относительно оси Ох; относительно оси Оу. 28. Какой вектор называется вектором нормали к плоскости? 29. Напишите уравнение плоскости, определяемой точкой, лежащей на ней, и вектором нормали. 30. Напишите общее уравнение плоскости. 31. Напишите уравнение плоскости, проходящей через три данные точки. 32. Напишите формулу для определения расстояния от точки до плоскости. 33. Что называется направляющим вектором прямой в пространстве? 34. Напишите канонические уравнения прямой в пространстве, проходящей через две данные точки.
Т е м а 1. 2. Элементы линейной алгебры. 1. Что называется определителем второго порядка? 2. Что называется определителем третьего порядка? 3. Назовите свойства определителей. 4. Что называется минором элемента определителя? 5. Что называется алгебраическим дополнением элемента определителя? 6. Назовите способы вычисления определителей. 7. Что называется матрицей? 8. Какая матрица называется единичной? 9. Что называется определителем матрицы? 10. Какая матрица называется невырожденной? 11. Как сложить две матрицы? 12. Как умножить матрицу на число? 13. В каком случае возможно перемножить две матрицы? 14. Что называется произведением двух матриц? 15. Всегда ли для произведения двух матриц справедлив переместительный закон умножения? Приведите примеры. 16. Какая матрица называется обратной данной матрице? 17. Как находится матрица, обратная данной? 18. Какое уравнение называется линейным? 19. Что называется системой линейных уравнений? 20. Что называется решением системы линейных уравнений? 21. Назовите правило Крамера решения системы n линейных уравнений с n неизвестными. В каком случае оно применимо? 22. Сформулируйте теорему Кронекера-Капелли. 23. При каком условии система линейных уравнений имеет единственное решение?
Т е м а 1. 3. Элементы векторной алгебры и аналитической геометрии в пространстве. 1. Какая величина называется скалярной? 2. Что называется вектором? 3. Что называется модулем вектора? 4. Какие векторы называются коллинеарными? 5. Какие векторы называются равными? 6. Как построить вектор, равный сумме двух или более векторов? 7. Как построить вектор, равный разности двух векторов? 8. Как умножить вектор на число? 9. Какой вектор называется единичным? 10. Какие векторы называются линейно независимыми? 11. Что называется базисом? 12. Что называется координатами вектора? 13. По какому правилу производится сложение векторов, заданных в координатной форме? 14. Как определить модуль вектора, заданного своими координатами? 15. Что называется скалярным произведением векторов? 16. Каков физический смысл скалярного произведения? 17. В каком случае скалярное произведение выражается положительным числом? Отрицательным числом? 18. Назовите свойства скалярного произведения векторов. 19. Чему равно попарное скалярное произведение одноименных ортов? 20. Чему равно скалярное произведение двух векторов, заданных своими координатами? 21. По какой формуле находится проекция одного вектора на другой? 22. Сформулируйте условие перпендикулярности двух векторов. 23. Дайте определение векторного произведения двух векторов. 24. Перечислите свойства векторного произведения. 25. Как вычислить векторное произведение двух векторов, заданных своими координатами? 26. Какие векторы называются компланарными? 27. Дайте определение смешанного произведения трех векторов. 28. Перечислите свойства смешанного произведения. 29. Как вычислить смешанное произведение трех векторов, заданных своими координатами? 30. Приведите условие компланарности трех векторов. 31. Как вычислить объем четырехгранной пирамиды по координатам ее вершин.
2. 1. 4. Задания для самостоятельной работы 1.Составить уравнение прямой, проходящей через точку А (2; 3) и составляющей с осью Ох угол 45◦. 2. Написать уравнение прямой, проходящей через точки А (4; 3) и В (16; -6). 3. Найти длину высоты BD в треугольнике с вершинами А (-3; 0), В (2; 5), С (3; 2). В задачах 4, 5вычислить определители: 4. 6.Решить систему уравнений двумя способами: 1) при помощи определителей (по формулам Крамера); 2) с помощью обратной матрицы.
7.Дан вектор AB = 3 i – 2 j + k. Определить координаты точки В, если А (–2; 1; 0). 8.Составить уравнение плоскости, проходящей через точку Мо (2; 3; -1) параллельно плоскости Содержание модуля. Тема 2. 1. Множество вещественных чисел. Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и гра- фики. Сложные и обратные функции. Числовая последовательность и ее предел. Существование предела монотонной ограниченной последовательности. Предел функции в точке и в бесконечности. Первый и второй замечательные пределы. Свойства пределов функции. Бесконечно малые величины. Их свойства. Сравнение бесконечно малых. Тема 2. 2. Непрерывность функции в точке и на интервале. Точки разрыва функции. Непрерывность основных элементарных функций. Свойства функции непрерывных на отрезке.
Вопросы для самоконтроля.
1. Какая величина называется постоянной? переменной? 2. Что называется функцией одной независимой переменной? 3. Что называется областью существования (определения) функции? 4. Назовите способы задания функции. 5. Какая функция называется явной? неявной? 6. Какая функция называется возрастающей? убывающей? 7. Какая функция называется четной? нечетной? 8. Какая функция называется периодической? 9. Какая функция называется элементарной? 10. Какие функции называются основными элементарными функциями? 11. Какая функция называется сложной? 12. Что называется интервалом знакопостоянства функции? 13. Какие функции называются взаимно обратными? Как построить график обратной функции по графику данной функции в системе декартовых координат? 14. Что называется числовой последовательностью? 15. Что называется пределом числовой последовательности? 16. Сформулируйте определение предела функции. 17. Сформулируйте теоремы о пределах функций. 18. Какая функция называется бесконечно малой? бесконечно большой? Какова зависимость между ними? 19. Перечислите свойства бесконечно малых функций. 20. Напишите формулы первого и второго замечательных пределов. 21. Какие логарифмы называются натуральными? 22. Сформулируйте определения односторонних пределов функции в точке. 23. Какая функция называется непрерывной в точке? на интервале? 24. Какая точка называется точкой разрыва первого рода? второго рода? 25. Перечислите свойства непрерывных на отрезке функций.
2. 2. 4. Задания для самостоятельной работы В задачах 1 – 6 вычислить пределы. 1. 4. Переменной Содержание модуля. Тема 3.1. Задачи, приводящие к понятию производной. Определение производной. Ее геометрический и механический смысл. Правила дифференцирования функций. Производные основных элементарных функций. Производная сложной и обратной функции. Производные высших порядков. Тема 3. 2. Дифференциал функции, его геометрический смысл. Инвариантность формы дифференциала. Дифференцирование функций, заданных параметрически. Применение дифференциала в приближенных вычислениях. Правило Лопиталя.Точки экстремума функции. Теорема Ферма. Теоремы Ролля, Лагранжа, Коши
Вопросы для самоконтроля. 1. Что называется производной функции? 2. Каков геометрический, физический смысл производной? 3. Какая функция называется дифференцируемой в точке? на интервале? 4. Как взаимосвязаны непрерывность и дифференцируемость функции в точке? 5. Напишите правила дифференцирования функций. 6. Напишите формулы дифференцирования основных элементарных функций. 7. Сформулируйте правило дифференцирования сложной функции. 8. Сформулируйте определение дифференциала функции. 9. Перечислите свойства дифференциала функции. 10. Каков геометрический смысл дифференциала функции?
2. 3. 4. Задания для самостоятельной работы В задачах 1 – 3 найти производные указанных функций. 1. 4.Найти дифференциал функции 5.Вычислить предел
Содержание модуля. Тема 4. 1. Условия монотонности функций. Экстремумы функции, необходимое условие. Достаточные условия. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке. Тема 4. 2.Исследование выпуклости графика функции. Точки перегиба. А симптоты графика функции. Общая схема исследования функции и построения ее графика. Уравнение касательной к кривой в данной точке. Вопросы для самоконтроля. 1. Сформулируйте теорему Ролля. Каков ее геометрический смысл? 2. Сформулируйте теорему Лагранжа. Каков ее геометрический смысл? 3. Сформулируйте достаточные признаки возрастания и убывания функции. 4. Какие точки называются стационарными точками функции? 5. Какие точки называются критическими точками функции? 6. Дайте определения максимума, минимума функции. 7. Что называется экстремумом функции? 8. Назовите необходимое условие экстремума функции. 9. Назовите достаточные признаки экстремума функции. 10. Какая кривая называется выпуклой? вогнутой? 11. Что называется точкой перегиба кривой? 12. Как найти интервалы выпуклости и вогнутости кривой? 13. Сформулируйте достаточный признак существования точки перегиба кривой. 14. Что называется асимптотой кривой? 15. Как найти вертикальные асимптоты кривой? 16. Как найти наклонные асимптоты кривой? 17. Назовите схему исследования функции и построения ее графика. 18. В каких случаях применяется правило Лопиталя при вычислении пределов?
2. 4. 4. Задания для самостоятельной работы 1. Найти интервалы возрастания и убывания функции
2. Исследовать на экстремум функцию 3. Исследовать на экстремум функцию 4. Открытый сверху резервуар с квадратным дном должен вмещать 108 литров воды. Каковы должны быть размеры резервуара, чтобы на его изготовление пошло наименьшее количество материала? 5. Найти интервалы выпуклости и вогнутости и точки перегиба кривой 6. Найти асимптоты кривой 7. Исследовать функцию
Содержание модуля. Тема 6. 1. Первообразная. Неопределенный интеграл, его свойства. Таблица основных интегралов. Интегрирование заменой переменной и по частям. Тема 6. 2. Интегрирование рациональных дробей. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных выражений. Вопросы для самоконтроля. 1. Сформулируйте определение первообразной функции. 2. Что называется неопределенным интегралом от данной функции? 3. Каков геометрический смысл неопределенного интеграла? 4. Перечислите свойства неопределенного интеграла. 5. Напишите формулы таблицы основных интегралов. 6. В чем сущность метода замены переменной при вычислении неопределенных интегралов? 7. Напишите формулу интегрирования по частям в неопределенном интеграле. 8. Укажите типы интегралов, вычисление которых целесообразно производить при помощи метода интегрирования по частям. 9. Изложите правило разложения правильной рациональной дроби на сумму простейших дробей. 10. Изложите методы интегрирования простейших рациональных дробей.
2. 6. 4. Задания для самостоятельной работы Вычислить неопределенные интегралы. 1. 4. 7.
Содержание модуля. Тема 7. 1.Задачи, приводящие к понятию определенного интеграла. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов. Методы вычисления определенного интеграла по формулам прямоугольников, трапеций, Симпсона. Несобственные интегралы с бесконечными пределами и от неограниченных функций, их основные свойства. Тема 7. 2. Приложение определенного интеграла.
Вопросы для самоконтроля. 1. Назовите задачи, приводящие к понятию определенного интеграла. 2. Напишите интегральную сумму для функции
3. Что называется определенным интегралом от функции 4. Каков геометрический смысл определенного интеграла? 5. Перечислите свойства определенного интеграла. 6. Чему равна производная от определенного интеграла с переменным верхним пределом интегрирования? 7. Напишите формулу Ньютона – Лейбница. 8. Напишите формулу замены переменной в определенном интеграле. 9. Чему равен интеграл 10. Напишите формулу интегрирования по частям в определенном интеграле. 11. Сформулируйте определение несобственного интеграла с бесконечными пределами интегрирования. 12. Сформулируйте определение несобственного интеграла от разрывной функции. 13. В каком случае несобственный интеграл называется сходящимся? расходящимся? 14. Как вычисляется площадь плоской фигуры в прямоугольной системе координат с помощью определенного интеграла? 15. Напишите формулы для вычисления объемов тел, образованных вращением плоской фигуры вокруг оси Ох; оси Оу.
2. 7. 4. Задания для самостоятельной работы Вычислить определенные интегралы. 1. 4.
Содержание модуля. Тема 8. 1. Функции нескольких переменных. Область определения. Предел функции. Непрерывность. Частные производные. Полный дифференциал, его связь с частными производными. Инвариантность формы полного дифференциала. Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала. Частные производные и полные дифференциалы высших порядков. Формула Тейлора. Неявные функции. Теоремы существования. Дифференцирование неявных функций. Тема 8. 2. Экстремумы функции нескольких переменных. Необходимое условие экстремума. Достаточные условия. Метод наименьших квадратов. Условный экстремум. Метод множителей Лагранжа. Примеры применений при поиске оптимальных решений.
Вопросы для самоконтроля.
1. Сформулируйте определение функции двух, трех и большего числа независимых переменных. 2. Что называется областью определения функции двух независимых переменных? 3. Каково геометрическое изображение функции двух переменных? 4. Сформулируйте определение предела функции двух переменных. 5. Что называется частным и полным приращениями функции двух переменных? 6. Какая функция двух переменных называется непрерывной в точке? в области? 7. Сформулируйте определение частных производных первого порядка функции двух независимых переменных. Каков их геометрический смысл? 8. Что называется полным дифференциалом функции двух переменных? 9. Как найти частные производные второго порядка функции двух переменных? 10. Что называется экстремумом функции двух независимых перемен- ных? 11. Сформулируйте необходимое условие существования экстремума функции двух переменных. 12. Сформулируйте достаточный признак экстремума функции двух переменных.
2. 8. 4. Задания для самостоятельной работы В задачах 1 – 4найти частные производные первого порядка указанных функций: 1. 4. В задачах 5 – 7найти частные производные второго порядка указанных функций. 5. В задачах 8 – 10исследовать на экстремум следующие функции: 8. 9. 10.
Содержание модуля. Тема 9. 1.Задачи, приводящие к понятию двойного интеграла (в частности, задача о вычислении объема цилиндрического тела). Двойной интеграл; его определение. Формулировка теоремы о существовании двойного интеграла. Свойства двойного интеграла. Теорема о среднем значении. Вычисление двойного интеграла по прямоугольной и произвольной областям сведением к повторному интегралу. Перемена порядка интегрирования в повторном интеграле. Переход в двойном интеграле к полярным координатам. Геометрические и физические приложения двойного интеграла: вычисление объемов тел и площадей, массы плоских фигур, моментов инерции и статистических моментов, координат центра тяжести плоских фигур. Тема 9. 2. Понятие о тройном интеграле. Задача о вычислении работы переменной силы. Определение криволинейного интеграла по координатам. Его простейшие свойства. Вычисление криволинейного интеграла путем сведения его к определенному интегралу. Криволинейный интеграл по дуге. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования (плоский случай). Нахождение функции двух переменных по ее полному дифференциалу. Интеграл по поверхности. Понятие о потоке векторного поля. Дивергенция. Формула Остроградского-Гаусса. Вопросы для самоконтроля. 1. Что называется двойным интегралом от функции двух переменных по данной области? 2. Дайте геометрическое толкование двойного интеграла. 3. Перечислите свойства двойного интеграла. 4. Укажите способы вычисления двойного интеграла в прямоугольной системе координат. 5. Как вычисляется двойной интеграл в полярной системе координат? 6. Напишите формулы для вычисления координат центра тяжести плоских фигур с помощью двойного интеграла. 7. Дайте определение тройного интеграла. 8. Как вычисляется тройной интеграл в прямоугольной системе координат? 9. Как вычисляется тройной интеграл в цилиндрической системе координат? 10. Напишите формулы для вычисления координат центра тяжести тела с помощью тройного интеграла. 11. Что называется криволинейным интегралом по координатам? 12. Перечислите свойства криволинейного интеграла. 13. Укажите способы вычисления криволинейного интеграла. 14. Напишите формулу Грина. 15. Сформулируйте условия независимости криволинейного интеграла по координатам от пути интегрирования. 16. Изложите способ нахождения функции двух переменных по ее полному дифференциалу.
2. 9. 4. Задания для самостоятельной работы. 1.Вычислить двойной интеграл Ответ: 86. В задачах 2, 3вычислить двойные интегралы. 2. 4.Переходя к полярным координатам, вычислить двойной интграл 5.Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболой Содержание модуля. Тема 10. 1. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Понятие об общем и частном решении. Интегральные кривые. Начальные условия Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения; линейные дифференциальные уравнения. Формулировка теоремы о существовании и единственности решения дифференциального уравнения первого порядка. Понятие об особом решении. Дифференциальное уравнение семейства плоских кривых, зависящих от одного параметра. Задача об ортогональных траекториях. Поле направлений дифференциального уравнения. Изоклины. Приближенное решение дифференциальных уравнений первого порядка (способ Эйлера). Вопросы для самоконтроля. 1. Что называется дифференциальным уравнением? 2. Что называется порядком дифференциального уравнения? 3. Что называется общим решением дифференциального уравнения первого порядка? 4. Что называется частным решением дифференциального уравнения 5. Каков геометрический смысл частного решения дифференциального уравнения первого порядка? 6. Приведите примеры дифференциальных уравнений с разделяющимися переменными. 7. Какое дифференциальное уравнение первого порядка называется линейным? уравнением Бернулли? Укажите способ их решения.
2. 10. 4. Задания для самостоятельной работы. В задачах 1 – 3найти общие интегралы следующих уравнений.
1. 3. В задачах 4, 5 найти частные решения уравнений, удовлетворяющие указанным начальным условиям. 4.
Модуль 11. Дифференциальные уравнения высших порядков. 2. 11. 1. Содержание модуля. Тема 11. 1. Понятие о дифференциальных уравнениях высших порядков, Общее и частное решения. Дифференциальные уравнения второго порядка, допускающие понижения порядка. Линейные однородные дифференциальные уравнения второго порядка. Свойства их решений. Линейно-независимые решения. Структура общего решения. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение. Запись общего решения в зависимости от корней характеристического уравнения. Тема 11. 2.Структура общего решения линейного неоднородного уравнения. Теорема наложения. Метод вариации произвольных постоянных. Отыскание частных решений линейных дифференциальных уравнений с постоянными коэффициентами в случае специальных правых частей уравнения (многочлен, Aekx, Acosnx+Bsinnx,). Линейные дифференциальные уравнения с пос
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.41.108 (0.012 с.) |

 . 5.
. 5. 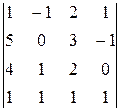 .
.
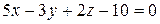 .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
. . 2.
. 2.  . 3.
. 3.  .
. .
.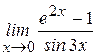 , используя правило Лопиталя.
, используя правило Лопиталя. .
.
 .
. .
. .
. и построить ее график.
и построить ее график. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
.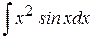 . 8.
. 8.  . 9.
. 9. 
 на отрезке
на отрезке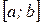 .
. на отрезке
на отрезке  ?
? , если
, если  . 2.
. 2.  . 3.
. 3. 
 . 5.
. 5.  . 6.
. 6.  .
. . 2.
. 2.  . 3.
. 3.  .
. .
. . 6.
. 6. 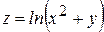 . 7.
. 7.  .
. .
. .
. .
.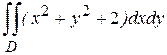 , если область D есть прямоугольник, ограниченный прямыми х=2, х=4, у=0, у=3.
, если область D есть прямоугольник, ограниченный прямыми х=2, х=4, у=0, у=3. . 3.
. 3.  .
. , где область D ограничена прямыми
, где область D ограничена прямыми  ,
,  и дугой окружности
и дугой окружности 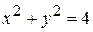 , лежащей в первой четверти.
, лежащей в первой четверти. и осью Ох.
и осью Ох. . 2.
. 2. 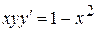 .
. .
.  ;
;  . 5.
. 5.  ;
;  .
.


