
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 8. Функции многих независимых переменных.Содержание книги
Поиск на нашем сайте
Содержание модуля. Тема 8. 1. Функции нескольких переменных. Область определения. Предел функции. Непрерывность. Частные производные. Полный дифференциал, его связь с частными производными. Инвариантность формы полного дифференциала. Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала. Частные производные и полные дифференциалы высших порядков. Формула Тейлора. Неявные функции. Теоремы существования. Дифференцирование неявных функций. Тема 8. 2. Экстремумы функции нескольких переменных. Необходимое условие экстремума. Достаточные условия. Метод наименьших квадратов. Условный экстремум. Метод множителей Лагранжа. Примеры применений при поиске оптимальных решений.
Методические указания по его изучению. После изучения по учебникам теоретического материала разберите реше- ние примера 17. Пример 17. Исследовать на экстремум функцию
Решение. Применим достаточный признак экстремума функции двух независимых переменных, состоящий в следующем. Пусть Обозначим
Если ∆ > 0, то Если ∆ < 0, в точке При ∆ = 0 – требуется дополнительное исследование. Находим частные производные
Решение системы уравнений
Следовательно, данная функция имеет две критические точки:
Найдем частные производные второго порядка:
Для точки Р 1 имеем А = −4, В = 9, С = −36, ∆ = 63. Так ∆ > 0 и А < 0, то в точке Р 1(−12, −6) данная функция имеет максимум: Для точки Р 2 имеем А = −4, В = 9, С = −4,5, ∆ = − 63. Так как ∆ < 0, то в этой точке экстремума нет.
Вопросы для самоконтроля.
1. Сформулируйте определение функции двух, трех и большего числа независимых переменных. 2. Что называется областью определения функции двух независимых переменных? 3. Каково геометрическое изображение функции двух переменных? 4. Сформулируйте определение предела функции двух переменных.
5. Что называется частным и полным приращениями функции двух переменных? 6. Какая функция двух переменных называется непрерывной в точке? в области? 7. Сформулируйте определение частных производных первого порядка функции двух независимых переменных. Каков их геометрический смысл? 8. Что называется полным дифференциалом функции двух переменных? 9. Как найти частные производные второго порядка функции двух переменных? 10. Что называется экстремумом функции двух независимых перемен- ных? 11. Сформулируйте необходимое условие существования экстремума функции двух переменных. 12. Сформулируйте достаточный признак экстремума функции двух переменных.
2. 8. 4. Задания для самостоятельной работы В задачах 1 – 4найти частные производные первого порядка указанных функций: 1. 4. В задачах 5 – 7найти частные производные второго порядка указанных функций. 5. В задачах 8 – 10исследовать на экстремум следующие функции: 8. 9. 10.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.247 (0.006 с.) |

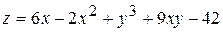 .
. - критическая точка функции
- критическая точка функции  , имеющей непрерывные частные производные первого и второго порядков.
, имеющей непрерывные частные производные первого и второго порядков. ,
,  ,
,  и составим определитель
и составим определитель .
. есть точка экстремума, причем при А > 0 – минимума, при А < 0 – максимума.
есть точка экстремума, причем при А > 0 – минимума, при А < 0 – максимума. и
и  , каждую из них приравняем к нулю и решаем полученную систему уравнений:
, каждую из них приравняем к нулю и решаем полученную систему уравнений: ;
;  .
. дает х 1 = − 12, у 1 = − 6,
дает х 1 = − 12, у 1 = − 6, ,
,  .
. ,
,  .
. ,
,  ,
,  .
.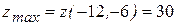 .
. . 2.
. 2.  . 3.
. 3.  .
. .
. . 6.
. 6. 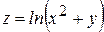 . 7.
. 7.  .
. .
. .
. .
.


