
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания по их выполнениюСодержание книги
Поиск на нашем сайте
Методические указания по выполнению контрольных работ Основной формой обучения студента-заочника является самостоятельная работа, состоящая из изучения материала, чтения учебника, решения задач, выполнения контрольной работы. В период лабораторно-экзаменационной сессии для студентов проводятся лекции и практические занятия, носящие обзорный характер. При изучении учебника следует воспроизводить на бумаге в форме конспекта основные моменты рассматриваемого вопроса программы, обращая особое внимание на определение основных понятий курса высшей математики, формулировки теорем, формулы. Работа над учебником должна сопровождаться решением задач. В соответствии с действующим учебным планом студенты изучают курс математики в течение первых двух лет при сроке обучения 5 лет и на первомкурсе при сокращенном сроке обучения и выполняют на каждом курсе по одной контрольной работе. При выполнении контрольной работы следует руководствоваться следующими указаниями: 1.Контрольная работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть написаны фамилия и инициалы студента, его шифр, дата отсылки работы в институт, домашний адрес. 2.Задачи контрольной работы следует располагать в порядке возрастания их номеров. Перед решением каждой задачи нужно полностью переписать ее условие. На каждой странице тетради нужно оставлять поля шириной 3-4 см для замечаний преподавателя. 3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых теорем и формул. Решение задач геометрического содержания должно сопровождаться чертежами (желательно на миллиметровой бумаге).Объяснения к решению задачи должны соответствовать обозначениям, приведенным на чертежах. 4. Контрольная работа должна выполняться самостоятельно, в противном случае студент лишается возможности проверить степень своей подготовленности по изучаемой дисциплине. 5. Получив из университета прорецензированную работу, студент должен исправить отмеченные преподавателем ошибки и недочеты. Если работа не зачтена, то в кратчайший срок следует выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом и первоначально выполненную работу.
6. В межсессионный период или во время лабораторно-экзаменационной сессии студент должен пройти на кафедре высшей математики собеседование по зачтенной контрольной работе. 7. Студент выполняет вариант контрольной работы, совпадающий с последней цифрой его учебного шифра. При сроке обучения 5лет математика изучается на первом и втором курсах, на каждом курсе выполняется одна контрольная работа. При этом, если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1. Если же предпоследняя цифра учебного шифра есть число четное (2, 4, 6, 8) или ноль, то номера задач даны в таблице 2. При сокращенном сроке обучения математика изучается на первом курсе и выполняется одна контрольная работа. При этом, если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 3. Если же предпоследняя цифра учебного шифра есть число четное (2, 4, 6, 8) или ноль, то номера задач даны в таблице 4. Таблица 1
Таблица 2
Таблица 3
Таблица 4
Задания для контрольных работ
В задачах 1 – 20 даны вершины треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах; 4) уравнение высоты CD и ее длину; 5) систему линейных неравенств, определяющих треугольник АВС. 1. A (0; 3), B (12; – 6), C (10; 8). 2. A (–8; 4), B (4; –5), C (2; 9). 3. A (–2; 2), B (10; –7), C (8; 7). 4. A (– 5; 0), B (7; 9), C (5; –5). 5. A (– 7; 0), B (5; 11), C (3; –3). 6. A (– 5; –3), B (7; 6), C (5; –8). 7. A (– 6; –2), B (6; 7), C (4; –7). 8. A (– 8; –4), B (4; 5), C (2; –9). 9. A (0; –1), B (12; 8), C (10; –6). 10. A (– 6; 1), B (6; 10), C (4; –4). 11. A (– 2; –4), B (10; 5), C (8; –9). 12. A (– 3; 0), B (9; 9), C (7; –5). 13. A (– 9; –2), B (3; 7), C (1; –7). 14. A (–5; 2), B (7; –7), C (5; 7). 15. A (–7; 5), B (5; –4), C (3; 10). 16. A (1; 2), B (13; – 7), C (11; 7). 17. A (–4; 1), B (8; –8), C (6; 6). 18. A (–7; 1), B (5; –8), C (3; 6). 19. A (–7; –1), B (5; –10), C (3; 4). 20. A (–3; 3), B (9; –6), C (7; 8).
В задачах 21 – 40 решить систему уравнений двумя способами: 1) при помощи определителей (по формулам Крамера); 2) с помощью обратной матрицы.
21.
23. 25. 27.
29.
31.
33.
35.
37.
39.
В задачах 41 – 60 даны координаты точек A, B, C, D. Требуется: 1) записать векторы АВ, АС, AD в системе орт и найти модули этих векторов; 2) найти величину угла между векторами АВ и АС;
3) найти площадь треугольника АВС; 4) найти объем пирамиды ABCD.
41. А (1; 1; 3), B (–4; 0; 3), C (–1; 5; 7), D (–2; –2; 9). 42. А (2; 2; 1), B (–3; 1; 1), C (0; 6; 5), D (–1; –1; 7). 43. А (–2; –1; 4), B (–7; –2; 4), C (–4; 3; 8), D (–5; –4; 10). 44. А (5; –1; 5), B (0; –2; 5), C (3; 3; 9), D (2; –4; 11). 45. А (6; 2; –2), B (1; 1; –2), C (4; 6; 2), D (3; –1; 4). 46. А (–1; 3; 6), B (–6; 2; 6), C (–3; 7; 10), D (–4; 0; 12). 47. А (1; 3; 3), B (2; 1; 5), C (12; 5; 13), D (–1; 3; 7). 48. А (4; 1; 1), B (5; –1; 3), C (15; 3; 11), D (2; 1; 5). 49. А (–3; 2;– 2), B (–2; 0; 0), C (8; 4; 8), D (–5; 2; 2). 50. А (5; 1; 2), B (6; –1; 4), C (16; 3; 12), D (3; 1; 6). 51. А (2; 2; 1), B (3; 0; 3), C (13; 4; 11), D (0; 2; 5). 52. А (3; 3; –1), B (4; 1; 1), C (14; 5; 9), D (1; 3; 3). 53. А (–1; 0; 2), B (0; –2; 4), C (10; 2; 12), D (–3; 0; 6). 54. А (6; 0; 3), B (7; –2; 5), C (17; 2; 13), D (4; 0; 7). 55. А (7; 3; –4), B (8; 1; –2), C (18; 5; 6), D (5; 3; 0). 56. А (0; 4; 4), B (1; 2; 6), C (11; 6; 16), D (–2; 4; 8). 57. А (0; 2; 5), B (–5; 1; 5), C (–2; 6; 9), D (–3; –1; 11). 58. А (3; 0; 3), B (–2; –1; 3), C (1; 4; 7), D (0; –3; 9). 59. А (–4; 1; 0), B (–9; 0; 0), C (–6; 5; 4), D (–7; –2; 6). 60. А (4; 0; 4), B (–1; –1; 4), C (2; 4; 8), D (1; –3; 10).
В задачах 61 – 80 вычислить указанные пределы.
61. а) в) 62. а) в) 63. а) в)
64. а) в)
65. а) в) 66. а) в) 67. а) в) 68. а) в) 69. а) в) 70. а) в) 71. а) в) 72. а) в) 73. а) в) 74. а) в) 75 а) в) 76. а) в) 77. а) в) 78. а) в) 79. а) в) 80. а) в) В задачах 81 – 100 найти производные данных функций.
81. а) в) 82. а) в) 83. а) в) 84. а) в) 85. а) в) 86. а) в) 87. а) в) 88. а) в) 89. а) в) 90. а) в) 91. а) в) 92. а) в) 93. а) в) 94. а) в) 95. а) в)
96. а) в) 97. а) в) 98. а) в) 99. а) в) 100. а) в)
В задачах 101 – 120 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости и точки перегиба графика функции; 6) найти асимптоты графика функции. 101. 104. 107. 110. 113. 116.
121. Каковы радиус основания R и высота Н открытого цилиндрического бака данного объема V, чтобы на его изготовление пошло наименьшее количество листового металла? 122. Найти наибольший объем цилиндра, полная поверхность которого равна S. 123. Найти наибольший объем конуса, образующая которого равна l. 124. Определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
125. Сумма двух положительных чисел равна а. Каковы эти числа, если сумма их кубов будет наименьшей? 126. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R. 127. На параболе 128. Из всех прямоугольников, вписанных в круг радиуса R, найти тот, который имеет наибольшую площадь. 129. Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения 18 м. При каком радиусе полукруга площадь сечения будет наибольшей? 130. Найти стороны прямоугольника наибольшей площади, который можно вписать в эллипс В задачах 131 – 150 вычислить неопределенные интегралы. 131. а) в) 132. а) в) 133. а) в)
в) 135. а) в) 136. а) в) 137. а) в) 138. а) в)
в) 140. а) в) 141. а) в) 142. а) в) 143. а) в) 144. а) в) 145. а) в) 146. а) в) 147. а) в) 148. а) в) 149. а) в) 150. а) в)
151. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 152. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями 153. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной астроидой 154. Найти длину дуги кривой 155. Найти длину дуги кривой 156. Найти длину одной арки циклоиды 157. Найти длину кривой 158. Найти площадь поверхности, образованной вращением вокруг оси Ох дуги кривой 159. Найти площадь поверхности, образованной вращением вокруг оси Ох одной полуволны синусоиды 160. Найти площадь поверхности, образованной вращением вокруг оси Ох астроиды 161. Найти координаты центра тяжести полуокружности
162. Найти координаты центра тяжести полуэллипса расположенного над осью Ох. 163. Найти координаты центра тяжести однородной плоской фигуры, ограниченной дугой синусоиды 164. Найти координаты центра тяжести однородной плоской фигуры, ограниченной эллипсом 165. Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболами 166. Вычислить площадь фигуры, ограниченной параболой
167. Вычислить площадь фигуры, ограниченной окружностью
168. Вычислить площадь фигуры, ограниченной эллипсом
169. Вычислить площадь фигуры, ограниченной кардиоидой
170. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной эллипсом
В задачах 171 – 190 функцию 171. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 . 22.
. 22.  .
. . 24.
. 24.  .
. . 26.
. 26.  .
. . 28.
. 28.  .
. . 30.
. 30.  .
. . 32.
. 32.  .
. . 34.
. 34.  .
. . 36.
. 36.  .
. . 38.
. 38.  .
. . 40.
. 40.  .
. ; б)
; б)  ;
;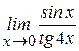 ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 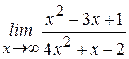 ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 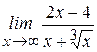 ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
.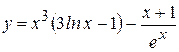 ; б)
; б)  ;
; .
. ; б)
; б) 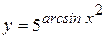 ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. ; б)
; б)  ;
; .
. . 102.
. 102.  . 103.
. 103.  .
. . 105.
. 105.  . 106.
. 106.  .
. . 108.
. 108.  . 109.
. 109.  .
. . 111.
. 111.  . 112.
. 112.  .
. . 114.
. 114.  . 115.
. 115.  .
. . 117.
. 117.  . 118.
. 118.  .
.
 . 120.
. 120.  .
. найти точку, наименее удаленную от прямой
найти точку, наименее удаленную от прямой  .
. .
. ; б)
; б)  ;
;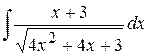 ; г)
; г) 
 .
.  ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
;  ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
.  ; б)
; б)  ;
;
 .
.  ; б)
; б)  ;
;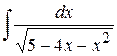
 .
. ; б)
; б)  ;
; ; г)
; г)  ; б)
; б)  ;
; ; г)
; г)  .
.  ; б)
; б)  ;
; ; г)
; г)  .
.  ; б)
; б)  ;
; ; г)
; г)  .
. 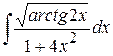 ; б)
; б) 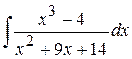 ;
; ; г)
; г)  .
.  ; б)
; б)  ;
; ; г)
; г)  ; б)
; б)  ;
; ; г)
; г)  .
.  ; б)
; б)  ;
; ; г)
; г)  .
.  ; г)
; г)  ; г)
; г)  ; б)
; б)  ;
; ; г)
; г)  .
.  ; б)
; б)  ;
; ; г)
; г)  .
.  ;
; ; г)
; г)  .
.  и
и 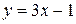 .
.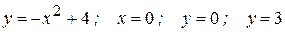 .
. .
. , отсеченной осью Ох.
, отсеченной осью Ох. , отсеченной прямой
, отсеченной прямой  .
. ,
,  .
. .
. от х = –4 до х = 2.
от х = –4 до х = 2. .
. , расположенной над осью Ох.
, расположенной над осью Ох. ,
, и
и  .
. и прямой
и прямой  .
. и параболой
и параболой  .
. .
. .
. исследовать на экстремум.
исследовать на экстремум.


