
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 10. Дифференциальные уравнения первого порядка.Содержание книги
Поиск на нашем сайте
Содержание модуля. Тема 10. 1. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Понятие об общем и частном решении. Интегральные кривые. Начальные условия Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения; линейные дифференциальные уравнения. Формулировка теоремы о существовании и единственности решения дифференциального уравнения первого порядка. Понятие об особом решении. Дифференциальное уравнение семейства плоских кривых, зависящих от одного параметра. Задача об ортогональных траекториях. Поле направлений дифференциального уравнения. Изоклины. Приближенное решение дифференциальных уравнений первого порядка (способ Эйлера). Методические указания по его изучению. После изучения по учебникам теоретического материала разберите реше- ние примера 21. Пример 21. Решить уравнение Решение. Разделим обе части уравнения на
тогда Так как искомая функция представима в виде произведения двух вспомогательных функций u и v, то одну из них можно выбрать произ- вольно. Выберем в качестве v какой-либо частный интеграл уравнения
Тогда для отыскания функции u имеем уравнение
Получаем два уравнения с разделяющимися переменными. Решаем первое уравнение:
Подставим
Следовательно,
Вопросы для самоконтроля. 1. Что называется дифференциальным уравнением? 2. Что называется порядком дифференциального уравнения? 3. Что называется общим решением дифференциального уравнения первого порядка? 4. Что называется частным решением дифференциального уравнения 5. Каков геометрический смысл частного решения дифференциального уравнения первого порядка? 6. Приведите примеры дифференциальных уравнений с разделяющимися переменными. 7. Какое дифференциальное уравнение первого порядка называется линейным? уравнением Бернулли? Укажите способ их решения.
2. 10. 4. Задания для самостоятельной работы. В задачах 1 – 3найти общие интегралы следующих уравнений.
1. 3. В задачах 4, 5 найти частные решения уравнений, удовлетворяющие указанным начальным условиям. 4.
Модуль 11. Дифференциальные уравнения высших порядков. 2. 11. 1. Содержание модуля. Тема 11. 1. Понятие о дифференциальных уравнениях высших порядков, Общее и частное решения. Дифференциальные уравнения второго порядка, допускающие понижения порядка. Линейные однородные дифференциальные уравнения второго порядка. Свойства их решений. Линейно-независимые решения. Структура общего решения. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение. Запись общего решения в зависимости от корней характеристического уравнения. Тема 11. 2.Структура общего решения линейного неоднородного уравнения. Теорема наложения. Метод вариации произвольных постоянных. Отыскание частных решений линейных дифференциальных уравнений с постоянными коэффициентами в случае специальных правых частей уравнения (многочлен, Aekx, Acosnx+Bsinnx,). Линейные дифференциальные уравнения с постоянными коэффициентами высших порядков. Системы линейных дифференциальных уравнений постоянными коэффициентами, простейшие приемы решения.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.130.96 (0.008 с.) |

 .
. :
: , убеждаемся, что оно – линейное. Положим
, убеждаемся, что оно – линейное. Положим  ,
, и уравнение преобразуется к виду
и уравнение преобразуется к виду  или
или  .
. . (1)
. (1) . (2)
. (2) ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
, 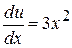 ,
,  ,
,  .
. - общее решение данного уравнения.
- общее решение данного уравнения. . 2.
. 2. 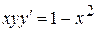 .
. .
.  ;
;  . 5.
. 5.  ;
;  .
.


