
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 2. Введение в математический анализ.Содержание книги
Поиск на нашем сайте
Содержание модуля. Тема 2. 1. Множество вещественных чисел. Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и гра- фики. Сложные и обратные функции. Числовая последовательность и ее предел. Существование предела монотонной ограниченной последовательности. Предел функции в точке и в бесконечности. Первый и второй замечательные пределы. Свойства пределов функции. Бесконечно малые величины. Их свойства. Сравнение бесконечно малых. Тема 2. 2. Непрерывность функции в точке и на интервале. Точки разрыва функции. Непрерывность основных элементарных функций. Свойства функции непрерывных на отрезке.
Методические указания по его изучению. После изучения по учебникам теоретического материала разберите реше- ние примера 5.
Пример 5. Вычислить пределы: а) в) д) Решение. а) При х = –3 числитель и знаменатель дроби, стоящей под знаком предела, обращаются в нуль, то есть имеем неопределенность
б) При стремлении х к бесконечности получаем неопределенность вида Деля числитель и знаменатель данной дроби на х 3 и применяя теоре- мы о пределах и свойства бесконечно малых функций, имеем:
в) При х = –3 получаем неопределенность вида
=
г) Пусть arcsin2x = y. Тогда 2 x = siny, y → 0 при х → 0. Тогда
Здесь применялась формула первого замечательного предела
д) При х → ∞ выражение, стоящее под знаком предела, есть неопределенность вида 1∞. Представим это выражение в виде суммы единицы и бесконечно малой при х → ∞ величины: Обозначим Таким образом, искомый предел имеет вид:
Здесь применялась формула второго замечательного предела
Вопросы для самоконтроля.
1. Какая величина называется постоянной? переменной? 2. Что называется функцией одной независимой переменной? 3. Что называется областью существования (определения) функции? 4. Назовите способы задания функции. 5. Какая функция называется явной? неявной? 6. Какая функция называется возрастающей? убывающей? 7. Какая функция называется четной? нечетной? 8. Какая функция называется периодической? 9. Какая функция называется элементарной? 10. Какие функции называются основными элементарными функциями? 11. Какая функция называется сложной? 12. Что называется интервалом знакопостоянства функции? 13. Какие функции называются взаимно обратными? Как построить график обратной функции по графику данной функции в системе декартовых координат? 14. Что называется числовой последовательностью? 15. Что называется пределом числовой последовательности? 16. Сформулируйте определение предела функции. 17. Сформулируйте теоремы о пределах функций. 18. Какая функция называется бесконечно малой? бесконечно большой? Какова зависимость между ними? 19. Перечислите свойства бесконечно малых функций. 20. Напишите формулы первого и второго замечательных пределов. 21. Какие логарифмы называются натуральными? 22. Сформулируйте определения односторонних пределов функции в точке. 23. Какая функция называется непрерывной в точке? на интервале? 24. Какая точка называется точкой разрыва первого рода? второго рода? 25. Перечислите свойства непрерывных на отрезке функций.
2. 2. 4. Задания для самостоятельной работы В задачах 1 – 6 вычислить пределы. 1. 4.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.126.199 (0.005 с.) |

 ; б)
; б) 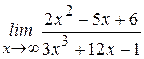 ;
; ; г)
; г)  ;
; .
. . Для ее устранения разложим числитель и знаменатель дроби на произведение линейных множителей и сократим дробь:
. Для ее устранения разложим числитель и знаменатель дроби на произведение линейных множителей и сократим дробь: .
. .Для устранения подобной неопределенности дробной рациональной функции следует числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов числителя и знаменателя дроби.
.Для устранения подобной неопределенности дробной рациональной функции следует числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов числителя и знаменателя дроби. .
. .
.

 .
. .
. .
. .
. . Отсюда
. Отсюда  ;
;  ;
;  . Если х → ∞, то у → - ∞.
. Если х → ∞, то у → - ∞. .
. .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
.


