Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определенного интеграла. Теорема Ньютона-Лейбница ⇐ ПредыдущаяСтр 9 из 9
Свойство 2. Определённый интеграл от суммы функций равен сумме неопределённых интегралов
Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла
Свойство 4. Если на отрезке
Свойство 5. Если
Свойство 6. Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак
Свойство 7. Для любых трёх чисел
Ньютона-Лейбница теорема выражает связь между определенным и неопределенным интегралами от интегрируемой функции f (x): если F (x) – любая первообразная для функции f (x), то имеет место формула Ньютона-Лейбница Этот факт (наряду с другими элементами интегрального и дифференциального исчислений) был независимо открыт и И. Ньютоном, и Г. Лейбницем примерно в одно и то же время – в последней четверти XVII века. Несобственные интегралы 1-го рода. Примеры В дальнейшем мы будем обычно иметь дело с несобственными интегралами от неотрицательных функций. Если функция
а) Для сходимости несобственного интеграла
Непосредственно найти такое число
б) Если на луче
В самом деле, из
Но функция
Из доказанного вытекает, что если
Пример 5. Исследуем на сходимость интеграл
Решение. Мы имеем
Пример 6. Исследуем на сходимость интеграл
Решение. Так как Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла. Примеры Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле. В этом параграфе нет ничего страшного или сложного. Единственная новизна состоит в вопросе, как поменять пределы интегрирования при замене. В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте. Пример 5 Вычислить определенный интеграл Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: Сначала готовим наш интеграл к замене:
Из вышеуказанных соображений совершенно естественно напрашивается замена:
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.221.204 (0.013 с.) |



 , где
, где  , функции
, функции  и
и  удовлетворяют условию
удовлетворяют условию 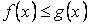 , то
, то
 и
и  - наименьшее и наибольшее значения функции
- наименьшее и наибольшее значения функции  , то
, то

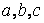 справедливо равенство
справедливо равенство
 , что справедливо равенство:
, что справедливо равенство:
 .
. .
.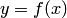 неотрицательна на луче
неотрицательна на луче 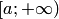 , то функция
, то функция  возрастает на этом луче. Поэтому она имеет предел при
возрастает на этом луче. Поэтому она имеет предел при 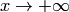 в том и только в том случае, когда ограничена. Отсюда получаем следующее утверждение:
в том и только в том случае, когда ограничена. Отсюда получаем следующее утверждение: от неотрицательной функции
от неотрицательной функции 
 , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция  была ограничена, т. е. чтобы нашлось такое число
была ограничена, т. е. чтобы нашлось такое число  , что
, что  для всех
для всех  .
.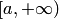 выполняется неравенство
выполняется неравенство  и интеграл
и интеграл  сходится, то сходится и интеграл
сходится, то сходится и интеграл 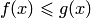 следует, что для любого
следует, что для любого  имеем:
имеем:
 возрастает, и потому ее предел при
возрастает, и потому ее предел при 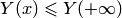 . Поэтому для всех
. Поэтому для всех 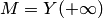 . А тогда на основании предыдущего утверждения интеграл
. А тогда на основании предыдущего утверждения интеграл 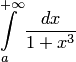 .
. при
при  . Но интеграл
. Но интеграл  сходится (см. пример 4). Поэтому сходится и исходный интеграл.
сходится (см. пример 4). Поэтому сходится и исходный интеграл.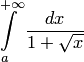 .
. при
при 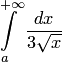 расходится (см. пример 4 при
расходится (см. пример 4 при  ), то расходится и заданный интеграл.
), то расходится и заданный интеграл.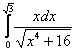
 . Но есть одна неувязочка, в табличном интеграле под корнем
. Но есть одна неувязочка, в табличном интеграле под корнем 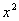 , а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.
, а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.

 .
. подынтегрального выражения, для этого находим дифференциал
подынтегрального выражения, для этого находим дифференциал  :
: