
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определенный интеграл как предел интегральной суммыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Естественный ход решения каждой из рассмотренных конкретных задач позволяет установить ту математическую операцию, с выполнением которой связано получение ответа во всех вопросах такого же характера. Пусть на отрезке [a, b] задана непрерывная функция y=f(x). 1). Заданный отрезок разделим на n промежутков (равных или неравных) точками a=x0<x1<x2<…<xn-1<xn=b, причем для всякого индекса i, принимающего целые значения от 1 до n, имеет место соотношение xi-1<xi. Выразим длину каждого из этих частичных промежутков: x1 - x0 = Δx1, x2 – x1 = Δx2,..., xn – xn-1 = Δxn. При этом обозначим длину наибольшего из них через λ. 2). В каждом из этих промежутков выберем произвольное число ξi так, что xi-1≤ ξi ≤ xi., и по каждому такому числу определим соответствующее значение функции f(ξi). Вычислим для каждого промежутка произведение f(ξi)Δxi.
f(ξ1)Δx1+ f(ξ2)Δx2+ f(ξ3)Δx3+...+ f(ξn)Δxn=. Такая сумма называется интегральной суммой. Построение интегральной суммы состоит в произвольном делении заданного отрезка [a, b] на частичные и произвольном выборе числа ξi на каждом отрезке. 4). Выполняется дробление каждого из имеющихся отрезков на более мелкие так, что длина наибольшего из них безгранично уменьшается (λ→0). При этом интегральная сумма становится переменной величиной, имеющей конечный предел, если заданная функция непрерывна, а отрезок [a, b] конечен. Этот предел называется определенным интегралом от функции f(x) на отрезке [a, b]. Соответствующее математическое выражение таково:
lim = λ→0 Знак ∫, представляющий растянутую S (начальную букву латинского слова «Summa»), символизирует здесь бесконечное увеличение числа слагаемых интегральной суммы. Буквы a и b, указывающие границы отрезка, на котором выполняется суммирование, называются пределами интегрирования. Таким образом, определенным интегралом функции от f(x) в границах от a до b называется предел интегральной суммы вида
при условии, что длина наибольшего частичного отрезка стремится к нулю. Поэтому естественным развитием понятия определенного интеграла является выбор целесообразного способа его вычисления. Такой способ, оказывается, дает операция интегрирования ввиду наличия связи между определенным интегралом и интегралом неопределенным.
ВОПРОС 9 Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция илифункционал, а вторая — область в множестве задания этой функции (функционала). Если существует указанный предел, то функция · · · · · ·
ВОПРОС 10 Связь между определенным и неопределенным интегралами. Формула Ньютона-Лейбница Определенный интеграл - это число, а физически - числовая интегральная характеристика некоторой области пространства, плоскости или интервала числовой оси. Здесь мы рассмотрим именно интервал числовой оси, поскольку связь между обоими типами интеграла можно установить только для интеграла от функции одной переменной. Итак, для каждого интервала числовой оси, для которого определена и непрерывна числовая функция, можно вычислить определенный интеграл, то есть число соответствующее данному интервалу и функции. Оставим левый конец интервала интегрирования фиксированным, а правый конец сделаем переменным. Тогда мы получим определенный интеграл с переменным верхним пределом интегрирования, который уже не будет числом, а будет функцией этого верхнего предела интегрирования. Доказано, что производная интеграла с переменным верхним пределом в точке равна значению подынтегральной функции в этой точке. Это означает, что интеграл с переменным верхним пределом есть первообразная подынтегральной функции. Определенный интеграл с фиксированным верхним пределом равен значению первообразной подынтегральной функции в точке, равной этому верхнему пределу. Отсюда легко вытекает, что определенный интеграл есть разность значений первообразных на концах отрезка интегрирования(теорема Ньютона-Лейбница). Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
11)обыкновенное дифференциальное уровнение n-го поядка-это уравнение вида F(x,y,y’,y’’…..yn)=0, где y=y(x)-неизвестная функция,зависящая от независимой переменной x, штрих(‘)означает дифференцирование по x.Решение может бытьвыражено в виде y=f(x,C1….Cn)где С1-Сn-производное постоянное.Дифференциальное уравнение вида y’=f(x)g(y) или M(x)N(y)dx+P(x)Q(y)dx=0, называется дифференциальным уравнением с разделяющимися переменными. В данных дифференциальных уравнениях каждая из функций зависит только от одной переменной,т.е. происходит разделение переменных.Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение,чтобы в одну часть уравнения входили только функции от x и dx, в другую часть уравнения только функции от y и dy.Затем полученное равнение нужно проинтегрировать обе части ∫ При делении обеих частей дифференциального уравнения на выражение,содержащее неизвестные x и y могут быть потеряны решения, обращающие это выражение в ноль.Дифференциально уравнение с разделяющимися переменными легко сводится к интегрированию.В общем случае получаем два неопределенных интеграла. Элементы теории вероятностей:события,происходящие в окружающем нас мире,можно разделить на три вида:достоверные,невозможные и случайные. Достоверным относительно комплекса условий называется событие,еотрое обязательно произойдет при существлении этого комплекса услови.Невозможным называется событие,которое заведомо не произойдет при осуществлени комплекса условий.Случайным относительно комплекса условий называется событие,которое при осуществлении указанного комплекса условий может либо произойти,либо не произойти.Случайными события называются тогда,когда в результате исполнения решение примет лишь одно возможное значение,заранее не известное и зависящее от случайных причин.Каждый случайная величина соответствует множество значений,которое она может принимать. 13)Правила сложения вероятностей:вероятность появления одного(безразличного какого) события из нескольких несовместимых событий равна сумме их вероятностей. Пусть n-общее число испытаний,m1-число случаев,благоприятствующих событию А, m2-число случаев,благоприятствующих событию В. Число случаев,благоприятствующих наступлению либо события А,либо события В,равно m1+m2.Тогда P(А или В)= Правила сложения вероятностей:вероятность совместимого появления независимых событий равна произведению их вероятностей. Т.к. события А и В независимы,то каждому из m1 случаев,благоприятствующих А, соответсвуют m2 случаев,благоприятствующих В.Таким образом, общее число равносложных событий равно m1m2. Аналогично,общее число равносложных событий равно n1n2, где n1 и n2-число равносложных событий соотвественно для А и В.Имеем P(А и В)= 14)Условная вероятность-вероятность одного события(А) при условии,что другое событие (В)уже произошло,записывается Р(А/В) =
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2092; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.26.149 (0.007 с.) |

 3). Составим сумму таких произведений по всем n промежуткам заданного отрезка:
3). Составим сумму таких произведений по всем n промежуткам заданного отрезка: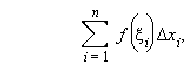

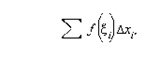
 называется интегрируемой на
называется интегрируемой на  .Обозначается:
.Обозначается: 
 – нижний предел.
– нижний предел. – верхний предел.
– верхний предел. - длина частичного отрезка.
- длина частичного отрезка. – интегральная сумма от функции
– интегральная сумма от функции  .
. - максимальная длина част. отрезка.
- максимальная длина част. отрезка.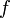 непрерывна на отрезке
непрерывна на отрезке  и
и  — ее любая первообразная на этом отрезке, то имеет место равенство
— ее любая первообразная на этом отрезке, то имеет место равенство 
 +∫
+∫  =C
=C
 P(A или B)=P(A)+P(B).
P(A или B)=P(A)+P(B). =
=  +
+  =P(A)*P(B)
=P(A)*P(B)



